Author: Sir James Jeans, M. A., D. Sc., Sc. D., LL. D., F. R. S.
[ p. 194 ] We have commented on the surprising emptiness of space: six specks of dust in Waterloo Station about represent the extent to which it is occupied by stars in its most crowded parts. The comment might well have taken another form. Six specks of dust contain, let us say, a thousand million million molecules. Our model of space is empty because this great number of molecules happens all to be aggregated into as few as six lumps. In real space the unit of aggregation is the star, and an average star contains about 1056 molecules — a number so large that it is quite useless to try to imagine it. The emptiness of space does not originate from any paucity of molecules; it originates from the circumstance that, apart from those which form the tenuous clouds of gas stretching from star to star, the molecules are aggregated together in the huge colonies we call stars, with about 1056 members to each. Why should the molecules in space herd together in this way, when the molecules in the rooms in which I am writing and you are reading do not?
Following a well-tried scientific method, we may attempt to discover why these aggregates have formed, by first examining what keeps them together now that they have formed. The earth’s atmosphere consists of about 1041 molecules. Why do they stay pressed down into an atmosphere instead of spreading out through space? The answer is of course provided by the earth’s gravitation. A bullet fired from the earth’s surface with a speed of 6.93 miles a second or more will fly off into space, because the earth’s gravitational pull is [ p. 195 ] inadequate to hold it back when it moves with so high a speed. But a bullet fired with a speed of less than 6.93 miles a second does not leave the earth; its speed is inadequate to take it clear of the earth’s pull. Thus the molecule-bullets which form the earth’s atmosphere, flying with speeds less than a third of a mile a second, have no chance at all of getting away. The earth’s gravitation continually pulls them back to earth, so that the earth retains its covering of air.
At rare intervals a molecule may experience a succession of exceptionally lucky collisions with other molecules, and so attain a speed of more than 6.93 miles a second. A molecule which arrives at the outside of the earth’s atmosphere with such a speed will leave the earth altogether, and join the interstellar crowd of stray molecules. The earth is continually shedding its atmosphere in this way, but calculation shews that the loss, even in millions of millions of years, is quite insignificant, so that we may regard the earth’s atmosphere as permanent.
It is the same with the sun. The sun’s heat has broken up the molecules of its atmosphere into their constituent atoms, and these move with an average speed of about 2 miles a second. But an atom-bullet would have to move at about 380 miles a second to escape altogether from the sun, so that the solar atoms remain to form an atmosphere.
If all the molecules of air in an ordinary room were collected into a bunch at the centre of the room, the ball of air so formed would of course exert a gravitational pull on its outermost molecules, of the same kind as the earth and sun exert on the molecules of their atmospheres. But, because the weight of this ball of air is so small, the intensity of its gravitational [ p. 196 ] pull would also be small; indeed it would be so feeble that a speed of about a yard a century would be enough to take the outermost molecules clear of it. As the molecules of ordinary air move at about 500 yards a second, such a ball of air would immediately scatter through the whole room. On the other hand, if the room were big enough to contain the sun, all its molecules could stay in a ball at the centre, just as they do in the sun. The outermost molecules would need a speed of at least 380 miles a second to escape, so that their actual speeds of 500 yards a second or so would be of no service to them.
Planetary atmospheres. In general the question of escape or no escape depends on the outcome of a battle between the molecular speeds of the outermost molecules, and the intensity of the gravitational hold which the remainder of the mass exerts on them. The solar system provides many examples of this. The moon has only a sixth as much gravitational hold over the molecules of an atmosphere as the earth has, with the result that any atmosphere the moon may ever have had, has escaped by now. Mercury has two-fifths of the earth’s gravitational hold, but, owing to its nearness to the sun, its sunward surface is very hot, with the consequence that its atmosphere also has escaped. The gravitational hold of Mars on its molecules is only a fifth of the earth’s, but its surface is cooler. Calculation shews that water-vapour and heavier molecules ought to remain, while the lighter molecules of helium and hydrogen ought to have escaped. This probably represents what has actually happened. The largest satellite of Saturn and the two largest satellites of Jupiter would exercise about the same gravitational hold as the moon, but as their surfaces must be enormously [ p. 197 ] colder than that of the moon, they ought to be able to retain atmospheres. Some observers claim to have seen indications of atmospheres on all three satellites. All the four major planets exert stronger gravitational holds over their molecules than the earth, and so retain their atmospheres with ease, while Venus, with approximately the same gravitational hold as the earth, also retains an atmosphere.
These considerations amply explain why the molecules of the stars must necessarily remain aggregated now that the aggregates have once been formed, but the question of how and why these aggregates formed in the first instance is far more complex. What, for instance, determined that there should be about 1056 molecules in each star rather than 1054 or 1058?
¶ Gravitational Instability
It is natural to enquire whether the forces which now keep a star together may not also have been responsible for its falling together in the first instance. This leads us to study the aggregating power of gravitation in some detail.
Five years after Newton had published his law of gravitation, Bentley, the Master of Trinity College, wrote him, raising the question of whether the newly discovered force of gravitation would not account for the aggregation of matter into stars, and we find Newton replying, in a letter of date December 10, 1692 :
It seems to me, that if the matter of our sun and planets, and all the matter of the universe, were evenly scattered throughout all the heavens, and every particle had an innate gravity towards all the rest, and the whole space throughout which this matter was scattered, was finite, the matter on the outside of this space would by its gravity [ p. 198 ] tend towards all the matter on the inside, and by consequence fall down into the middle of the whole space, and there compose one great spherical mass. But if the matter were evenly disposed throughout an infinite space, it could never convene into one mass ; but some of it would convene into one mass and some into another, so as to make an infinite number of great masses, scattered great distances from one to another throughout all that infinite space. And thus might the sun and fixed stars be formed, supposing the matter were of a lucid nature.
An exact mathematical investigation on which I embarked in 1901, not only confirms Newton’s conjecture in general terms, but also provides a method for calculating what size of aggregates would be formed under the action of gravitation.
The Formation Of Condensations. You stand in the middle of a room and clap your hands. In common language you are making a noise; the physicist, in his professional capacity, would say you are creating waves of sound. As they approach one another, your hands expel the intervening molecules of air. These stampede out, colliding with the molecules of outer layers of air, which are in turn driven away to collide with still more remote layers ; the disturbance originally created by the motion of your hands is carried on in the form of a wave. Although the individual molecules have an average speed of 500 yards a second, the zig-zag quality of their motions reduces the speed of the disturbance, as we have already seen, to about 370 yards a second — the ordinary velocity of sound. As the disturbance reaches any point the number of molecules there becomes abnormally high, for the stampeding molecules add to the normal quota of molecules at the point. This of course produces an excess of pressure. It is this excess pressure acting on [ p. 199 ] my ear-drum that transmits a sensation to my brain, so that I hear the noise of your clapping your hands.
This excess of pressure cannot of course persist for long, so that the excess of molecules which produces it must rapidly dissipate. It is thus that the wave passes on. Yet there is one factor which militates against its dissipation. Each molecule exerts a gravitational pull on all its neighbours, so that where there is an excess of molecules, there is also an excess of gravitational force. In an ordinary sound wave this is of absolutely inappreciable amount, yet such as it is, it provides a tiny force holding the molecules back, and preventing them scattering as freely as they otherwise would do. When the same phenomenon occurs on the astronomical scale, the corresponding forces may become of overwhelming importance.
Let us speak of the gas in any region of space where the number of molecules is above the average of the surrounding space, as a “condensation.” Then it can be proved that, if a condensation is of sufficient extent, the excess of gravitational force may be sufficient to inhibit scattering altogether. In such a case, the condensation may continually grow through attracting molecules into it from outside, whose molecular speeds are then inadequate to carry them away again.
Whether this happens or not will depend of course on the speed of molecular motion in the gas, as well as on the size of the condensation. But it will not depend at all on the extent to which the process of condensation has proceeded. By doubling the excess number of molecules in any condensation, we double the extent to which condensation has proceeded. In so doing, we double the gravitational pull tending to increase the condensation, but we also double the excess pressure [ p. 200 ] which tends to dissipate it; we double the weights on each side of the balance, but the balance still swings in the same direction. If once conditions are favourable to its growth, a condensation goes on growing automatically until there are no further molecules left for it to absorb.
The greater the extent in space of a condensation, the more favourable conditions are to its continued growth. Other things being equal, a condensation two million miles in diameter will exert twice the gravitational force of a condensation one million miles in diameter, but the excess pressures are the same in the two cases. Thus, the larger a condensation is the more likely it is to go on growing, and by passing in imagination to larger and larger condensations we must in time come to condensations of such a size that they are bound to keep on growing. Nature’s law here is one of unrestricted competition. Nothing succeeds like success, and so we find that condensations which are big to start with have the capacity of increasing still further, while those which are small merely dissipate away.
Suppose now that an enormous mass of uniform gas extends through space for millions of millions of miles in every direction. Any disturbance which destroys its uniformity may be regarded as setting up condensations of every conceivable size.
This may not seem obvious at first; it may be thought that a disturbance which only affected a small area of gas would only produce a condensation of small extent. Such an argument overlooks the way in which the gravitational pull of a small body acts throughout the universe. The moon raises tides on the distant earth, and also tides, although incomparably less in amount, on the most distant of stars. Each time [ p. 201 ] the child throws its toy out of its baby-carriage, it disturbs the motion of every star in the universe. So long as gravitation acts, no disturbance can be confined to any area less than the whole of space. The more violent the disturbance which creates them, the more intense the condensations will be to begin with, but even the smallest disturbance must set up condensations, although these may be of extremely feeble intensity. And we have seen that the fate of a condensation is not determined by its intensity but by its size. No matter how feeble their original intensity may have been, the big condensations go on growing, the small ones disappear. In time nothing is left but a collection of big condensations. The mathematical analysis already referred to shews that there is a definite minimum weight such that all condensations below this weight merely dissipate away into space. To a good enough approximation for our present purpose, this minimum weight is such that if a tenth of this weight of gas were isolated in space, and all the rest of the gas annihilated, the molecules would just and only just fail to escape from its surface[1].
We may say that the original uniformly distributed mass of gas was “unstable” because any disturbance, [ p. 202 ] however slight, causes it to change its configuration entirely; it had the dynamical attributes of a stick balanced on its point, or of a soap-bubble which is just ready to burst.
Primaeval chaos. These general theoretical results may now be applied to any mass of gas we please. Let us begin by applying them to Newton’s hypothetical “matter evenly disposed throughout an infinite space.” We return in imagination to a time when all the substance of the present stars and nebulae was spread uniformly throughout space ; in brief, we start from the primaeval chaos from which most scientific theories of cosmogony have started. Hubble has estimated that if the whole of the matter in those parts of the universe we know were redistributed evenly throughout space, the gas so formed would have only about 1.5 x 10-31 times the density of water. This estimate is almost certainly on the low side, even as representing present conditions, and in trying to reconstruct the primaeval gas we must add something to allow for the molecules and atoms which have melted away into radiation in the intervening period. On the whole, perhaps 10-30 is not an unreasonable density to assign to the hypothetical primaeval nebula. It is almost inconceivably low. In ordinary air, at a density of one eight-hundredth that of water, the average distance between adjoining molecules is about an eight-millionth part of an inch; in the primaeval gas we are now considering, the corresponding distance is two or three yards. The contrast again leads back to the theme of the extreme emptiness of space.
What is the minimum weight of condensation that would persist in this primaeval gas?
Calculation shews that if ordinary air were attenuated [ p. 203 ] to this extraordinary degree, no condensation could persist and continue to grow unless it had at least 62½ million times the weight of the sun; any smaller weight of gas would exert so slight a gravitational pull on its outermost molecules, that their normal molecular speeds of 500 yards a second would lead to the prompt dissipation of the whole condensation.
We can carry out similar calculations with reference to other assumed densities of gas, and other molecular velocities. The following table shews the weights of condensations which would be formed in primaeval masses of chaotic gas having the densities shewn in the first column, and the various molecular velocities mentioned at the heads of the remaining columns. In each case the weights of the condensations are given in terms of the weight of the sun :
| Density in terms of water | Mol. vel. of 500 yards a sec. | Mol. vel. of 1000 yards a sec. | Mol. vel. of 2000 yards a sec. | Mol. vel. of 3000 yards a sec. |
|---|---|---|---|---|
| 10-29 | 25,000,000 | 200,000,000 | 1,500,000,000 | 5,000,000,000 |
| 10-30 | 62,500,000 | 500,000,000 | 4,000,000,000 | 13,000,000,000 |
| 1.5 x l0-31 | 100,000,000 | 1,300,000,000 | 10,000,000,000 | 30,000,000,000 |
All known stars have weights comparable with that of the sun. Thus if, as Newton conjectured, the stars first came into being as condensations of this kind, then the entries in this table ought to be comparable with unity. Newton’s conjecture, in the form in which we have just considered it, is clearly untenable, since all the calculated weights are many millions of times that of the sun. If there ever existed a primaeval chaos of the kind we are now considering, it would not condense into stars, but into enormously more massive condensations, each having the weight of millions of stars.
[ p. 204 ]
¶ The Birth Of The Great Nebulae
Now it is significant that bodies are known in space having weights equal to those just calculated, namely the great extra-galactic nebulae. There are two nebulae whose weights can be determined with fair accuracy, namely the Great Nebula in Andromeda (Plate IV, p. 30) and the nebula N.G.C. 4594 in Virgo (Plate XV). Hubble estimates these to be as follows :
| Nebula | Weight |
|---|---|
| Nebula M 31 | weight = 3500 million times that of sun |
| Nebula N.G.C. 4594 | „ = 2000 |
These estimates are again probably both on the low side, but their general order of magnitude is such as to suggest that the condensations which would first be formed out of the primaeval nebula must have been the great extra-galactic nebulae, and not mere stars. It is of course at best only a conjecture that the great nebulae were formed in this manner — if for no other reason because we can never know whether the hypothetical primaeval nebula even existed — but it seems the most reasonable hypothesis we can frame to explain the fact that the present nebulae exist. These nebulae are so generally similar to one another that it seems likely that they must all have been produced by the action of the same agency, and that which we have just considered provides a reasonable explanation which, apart from the postulated existence of the continuous primaeval nebula, is based on verae causae.
The great nebulae are of course not exactly similar, and our next inquiry must be as to the origin of their differences.
If the condensations in the primaeval gaseous nebula [ p. 205 ] had formed and contracted in an absolutely regular fashion, the final product would be an array of perfectly equal and similar masses of gas spaced with perfect regularity. But nature is seldom as regular as this; and we need not be surprised that the observed nebular array is not evenly spaced, or that its members are neither equal in weight, nor symmetrically arranged. As the original condensations in the primaeval gas contracted, they must have produced currents, and these would hardly be likely to occur absolutely symmetrically. If the motion in each mass of condensing gas had been directly towards the centre of the condensation at every point, the final result would have been a spherical nebula devoid of all motion, but any less symmetrical system of currents would result in a spin being given to each contracting mass. This spin would no doubt be very slow at first, but the well-known principle of “conservation of angular momentum ” requires that, as a spinning body contracts, its rate of spin must increase. Thus when the process of condensation was complete, the final product would be a series of nebulae rotating at different rates.

Nebula it rotation. And this is exactly what is observed; so far as our evidence goes the nebulae are in rotation, and at different rates. The various parts of the surface of any rotating mass necessarily have different speeds in space. The sun for instance rotates about its axis in such a direction that the surface we see is moving always from east to west; as a result the eastern limb is always advancing towards the earth, while the western limb is receding from us. A spectroscope turned on to different parts of the sun’s surface in succession at once reveals these differences of speed; they not only assure us of the sun’s rotation, [ p. 206 ] but enable us to measure its amount. The nebulae may be examined in the same way, and the examination shews that a large number of them are rotating with the perfectly regular motion of a solid body — a spinning-top, for instance. Measured by terrestrial standards their rates of rotation seem extraordinarily slow ; for instance the Great Nebula M 31 in Andromeda requires about 19,000,000 years to make a complete rotation, but this apparent slowness is an inevitable result of the huge size of the nebula. Even to get round once in 19,000,000 years, the outer parts of the nebula have to move with speeds of hundreds of miles a second.
A few of the nebulae are quite irregular in shape, but the majority have regular shapes, and it is highly significant that these are precisely the shapes which, it can be calculated mathematically, would be exhibited by rotating masses of gas. Actually there is a far stronger case than this for supposing the nebulae to be rotating masses of gas. From the purely observational evidence of surface-brightness and other characteristics, Hubble found that nearly all of these nebulae could be arranged in a single linear sequence — they could be arranged in order like beads on a string. And this order proved to be practically identical with the sequence which had previously been calculated, by purely theoretical methods, for the configurations of masses of gas rotating at gradually increasing rates of speed.
Let us examine this sequence of theoretical configurations in their natural order.
A mass of gas which was not rotating at all would of course assume a spherical shape under its own gravitation. A number of perfectly spherical nebulae are [ p. 207 ] known; a typical example is shewn in fig. 1 on Plate XVI.

With slight rotation the mass assumes the shape of a slightly flattened orange, like the earth or Jupiter. Nebulae of this shape are also known in abundance; an example is shewn in fig. 2 on the same plate.
With a higher degree of rotation the degree of flattening increases, but theoretical calculation shews that the orange shape is soon departed from. The equator first begins to shew a pronounced bulge, until finally, with sufficient rotation, this develops into a sharp edge, the rotating mass now being shaped like a double-convex lens. This prediction of theory is abundantly confirmed by observation, a large number of these lens-shaped nebulae being observed in the sky. An example is shewn in fig. 3 on Plate XVI.
The next step is somewhat sensational. Further rotation does not, as might be expected, result in still further flattening. Up to now, each increase in rotation has made the bulge on the equator sharper, but this is now as sharp as it can be. Theory shews that the flattening has also proceeded to the utmost possible limit, and that the next stage must consist in matter being ejected through the sharp edge of the equator and spread throughout the equatorial plane. Here again observation confirms theory; figs. 4 and 5 (Plate XVI) shew types of nebulae actually observed, the former being the nebula in Virgo which we have already had under discussion.
The comparatively thin layer of gas which now lies in the equatorial plane is similar in one respect at least to Newton’s matter “evenly disposed throughout an infinite space.” Disturbances can be set up in it in a variety of ways, and any disturbance, no matter how [ p. 208 ] slight, must result in the creation of a series of condensations. As before, those below a certain limit of size disappear of themselves, while those above this limit continually increase in intensity until they have absorbed all the gas in the equatorial plane. Again, as with the hypothetical primaeval chaos, we can calculate the minimum size of condensation which can be expected to have a permanent existence, and once again the result proves to be highly significant.
Hubble’s estimates of the total weights of two conspicuous nebulae have already been given. As the distances, and therefore also the sizes, of both these nebulae are known, it is an easy matter to calculate the average density of the gas throughout the whole nebula. The average density in M 31 is found to be about 5 x 10-22 of that of water; the corresponding number for N.G.C. 4594 is 2 x 10-21. These figures give us some idea of the density of matter in the outer regions of the nebulae. Although these densities are about a thousand million times as great as the estimated density of the original primaeval nebula of space, they are still almost inconceivably low. There is still only about one molecule to the cubic inch, and a single breath from the lungs of a fly could fill a large cathedral with air of this density.
On proceeding to calculate the weights of the smallest condensations which could form and persist in a gas of this low density, we obtain the results shewn in the following table. The molecular velocities are taken rather low, so as to allow for the cooling which must occur when the gas is spread out in the equatorial plane of the nebula.
Again the weights of the condensations are given in terms of the weight of the sun. And the significant fact [ p. 209 ] emerges that most of the entries in the table represent weights comparable with that of the sun. We are dealing with stellar weights at last; the condensations which must form in the outer regions of the great nebulae will have weights comparable with those of the stars.
| Density in terms of water | Mol. vel. of 100 yards a sec. | Mol. vel. of 300 yards a sec. | Mol. vel. of 500 yards a sec. |
|---|---|---|---|
| 10-21 | 1.7 | 36 | 220 |
| 10^-22 ^ | 5 | 130 | 625 |
| l0-23 | 17 | 360 | 2200 |
¶ The Birth Of Stars
And indeed there can be but little doubt that the process we have just been considering is that of the birth of stars. Even a casual glance at photographs of nebulae suffices to shew that the matter which has been ejected into the equatorial plane of a nebula does not lie uniformly spread out in that plane; it is seen to have fallen into bunches, knots or condensations. These are apparent enough in many of the nebular photographs already shewn, but they can be seen still more clearly in nebulae which are viewed nearly full on, such as for instance the two striking nebulae shewn in Plates XVII and XVIII.
These bunches are invariably too large to be interpreted as single stars; they are more probably groups of stars. In the largest telescopes they break up into great numbers of points of light in the way already exhibited in Plate XI (p. 70). We have already mentioned the reasons which compel us to regard these points of light as actual stars, the principal being that some of them shew the characteristic light-fluctuations [ p. 210 ] of the Cepheid variables. It is not altogether clear whether the stars are formed directly as condensations in the equatorial plane of the nebula, or whether larger condensations form first, namely the bunches observable in nebular photographs, which subsequently form smaller condensations, the stars. On the whole it seems likely that there are two processes involved — first the break-up of the nebular matter into big condensations, and then the break-up of these big condensations into stars. Such a succession of processes might well accompany a gradual cooling of the matter, and it is of course possible that there are even more than two processes involved. There is no need to form a final opinion on this at present, as it is in no way essential to the progress of the main argument.
A collection of nebular photographs enables us to follow nebular evolution from the earliest stages shewn in Plate XVI (p. 207), through the first appearance of granular bunches, such as are shewn in Plate XVII, and the first distinct appearance of stars shewn in Plate XVIII, down to the later stages, such as are shewn in Plates XIX and XX, in which the nebula appears to be but little more than a cloud of stars. Hubble has found it possible to follow the sequence still further, and can trace a continuous transition from the nebulae of this last type to pure star-clouds such as the Greater and Lesser Magellanic Clouds shewn in Plate XXI.
Thus the stars appear to have been born in much the same way as we have conjectured that their parents, the great nebulae, had been born before them, namely, through the agency of what is generally known as “Gravitational Instability.” This causes any mass of chaotic gas to break up into detached condensations, [ p. 211 ] and, the more tenuous the original gas, the greater the weights of the condensations formed out of it. The original primaeval nebula was of such low density that the condensations which formed in it weighed thousands of millions of times as much as the sun. These increased their density so much in contracting that when their rotation caused them to eject gaseous matter, this condensed into masses of stellar weight which we believe actually to be stars.


We have less certain knowledge of the former process than of the latter. Our only reason for thinking that the former process ever occurred is that the extragalactic nebulae now exist. There is no evidence that the primaeval chaotic nebula ever existed, beyond the fact that the hypothesis of its previous existence leads to a very satisfactory explanation of the present nebulae existing as they now do. On the other hand, we not only know that the stars exist : we also know that the masses of gas exist out of which theory shews that stars must necessarily be born. They are the tenuous equatorial fringes of the great nebulae. Our telescopes shew us both the nebular fringes and the stars, and we can almost study the actual process of birth.
The Galactic System Of Stars. If this is the true account of the birth of the stars, then our sun and its companions in space must have been born out of a rotating nebula. Observation gives strong support to this conclusion. Since the time of the Herschels, it has been a matter of frequent comment that the galactic system has the general shape of the extragalactic nebulae, the galactic plane of course representing the equatorial plane of the original nebula. On purely observational grounds, present-day astronomical thought is moving rapidly towards regarding [ p. 212 ] the whole galactic system either as a rotating nebula or the remains of one. It is even possible that this may still retain a central region which is as yet uncondensed into stars. In the direction of the constellations Scorpio and Ophiuchus are dark clouds which may either veil the centre of the system or may conceivably be the centre itself.
In 1904, Kapteyn found that the directions of motion of the stars in the vicinity of the sun were not distributed at random. The stars appeared to prefer to move to and fro along a certain direction in the galactic plane rather than in other directions — “star- streaming,” he called it. This peculiarity in the motion of the stars may be expected to throw some light on their origin.
Each star moves in a complicated orbit under the gravitational attraction of all the other stars of the galactic system. It is not possible to calculate this orbit in detail. The orbit of a planet round the sun is easily calculated because only two bodies are involved, the planet and the sun. But even when there are only three bodies involved, it is impossible to calculate the orbits that each describes under the attractions of the other two jointly: this is the famous problem of three bodies, which has never been solved. When, as in the galactic system, thousands of millions of stars are involved, it is naturally useless to try to calculate the orbit of each star — -it would be as futile as trying to calculate the path of each molecule in a gas.
Yet the same statistical methods which give us useful information as to the properties of a gas may be applied to studying the motions of the stars. There are so many stars that we do not trouble about individuals at all, we just treat them all together as a crowd. To [ p. 213 ] treat them as individuals would be as though the railway company tried to forecast the Bank Holiday traffic from London to Brighton by considering the finances, habits and psychology of each individual Londoner.


Without going into individual details, we can see that each star must describe an orbit which, after touring round a large part of the galaxy, comes back to somewhere near its starting point. Calculation shews that each such circuit must take hundreds of millions of years to complete. Even so, the stars will mostly have performed several complete circuits while the earth has been in existence, and if we are right in supposing the ages of the stars to be millions of millions of years, each star must have toured round the galaxy several thousands of times. We should accordingly expect the galaxy to have assumed a definite permanent shape by now; the distribution of stars in its different parts ought to have become something like steady, and the stars ought to have settled down to a state approximating to one of steady motion.
Statistical methods of investigation shew that there is not a great number of possible arrangements for a system of stars which has lived long enough to attain a steady state. If the system as a whole has no rotation at all, there is only one arrangement; the stars form a globular mass with perfect symmetry in all directions. The observed globular clusters (Plate IX, p. 63) provide good approximations to this type of formation, although Shapley has found that the maj ority are not absolutely spherical in shape. If the system as a whole is endowed with rotation, the possible configurations are all of a flattened symmetrical shape, like a coin, a watch or a round biscuit — in other [ p. 214 ] words a system of stars in rotation must be shaped pretty much as we believe the galaxy to be shaped. Furthermore the motions of these stars must shew “star-streaming” of precisely the kind discovered by Kapteyn.

Thus both the shape of the galaxy and the peculiarities of motion of its stars indicate that the galactic system as a whole must be in a state of rotation. And, as we have seen (p. 67), recent observational researches by Oort, Plaskett and others make it fairly certain that the rotation required by theory is an actual fact. The motions of the stars indicate that the whole galactic system is rotating at a rate which varies from one region to another, being about one revolution every 230 million years in the vicinity of the sun. And the hub of this gigantic wheel is found to coincide very closely with the spot which Shapley had previously fixed as the geometrical centre of the galactic system from his researches on the distribution of the globular clusters.
Thus, since rotation cannot be generated out of nothing, all the phenomena agree in shewing that the galactic system must have been born out of a rotating body. We are acquainted with only one type of astronomical body which is of sufficient size to turn into a galactic system, namely the great nebulae, and as the majority of these are believed, and some are known with certainty, to be in rotation, it seems reasonable to conclude that the galactic system must have been born out of a nebula, unless indeed its structure is still such that we should even now describe it as a nebula if we saw it from the great distance from which we view the other great nebulae. The observed period of rotation of the galactic system, of the order of 230 million years, is [ p. 215 ] substantially longer than the period, either known or suspected, of any of the nebulae, but the dimensions of the galactic system are also greater than those of any known nebula, and the two facts hang together. Again, the number of stars in the galactic system is probably substantially higher than in any nebula, as also is the total weight of these stars[2]. All this makes it clear that if the galaxy is, or ever has been, one of the great nebulae, it must have been one of unusual size and weight.
We have seen how the sun and all the stars are continually losing weight as the result of their emission of radiation. It follows that the total weight of the galactic system is for ever decreasing, and as a consequence its gravitational hold on its constituent stars is continually weakening. If this gravitational hold were suddenly to vanish altogether, each star would replace its present curved path by a perfectly straight line, along which it would travel at its present speed, undeflected by any gravitational forces from other stars, so that the stars which now constitute the galactic system would soon be scattered through the whole of space. In brief, if the gravitational pull of the stars were suddenly abolished, the galaxy would begin to expand at a great rate.
Although this is not likely to happen, the gradual abolition of the gravitational pull of the stars, as they turn their weight into radiation, must cause the galaxy to expand all the time at a slow rate : calculation suggests that its present rate of expansion would double its size in about 30 million million years. The expansion [ p. 216 ] must have been far more rapid in the past, when the stars were full of youthful vigour and squandered their substance more lavishly than now, so that it seems probable that the galactic system was substantially smaller and more compact in the past than now, and the original nebula probably smaller still.
We have seen how the stars in the great nebulae appear to be congregated in bunches or clusters. The globular clusters in the galactic system may possibly be bunches of stars of the same general type, which have remained undisturbed by other groups of stars and so have assumed the globular form under their own attraction — just as a mass of gas would do. Shapley finds that these clusters lie somewhat outside the galactic plane ; it looks as though they were broken up or disorganised in travelling through this plane, where they would encounter other stars.
By contrast groups of stars of the type generally described as moving clusters — the Pleiades, the Hyades, the stars of the Great Bear and a crowd of others voyaging in company with them through space — are generally found to move in the galactic plane. These may quite possibly represent the final vestiges of globular clusters which have been broken up by interaction with other stars, all except the most massive members having been knocked out of formation. Mathematical analysis shews that the interaction between the stars of such moving clusters and other stars in the galactic plane would cause each cluster to assume the shape of a flat biscuit or watch, of diameter equal to 2½ times its thickness. It is significant that the majority of the moving clusters shew a flattening of this kind, its amount agreeing tolerably well with the calculated value. It is even conceivable that the [ p. 217 ] “local cluster” surrounding the sun (p. 65) may be the remains of such a bunch of stars.
The motions of these clusters may also induce a further flattening, in a direction perpendicular to their motion. Some clusters shew this further flattening, the Ursa Major cluster being a striking example.
¶ The Birth Of Binary Systems
In discussing the way in which nebulae might be born out of chaos, we noticed that the existence of currents in the primordial medium would endow the resulting nebulae with varying amounts of rotation. For the same reason the children of the nebulae, the stars, must also be endowed with rotation at their birth. There is a further reason for such rotation. The general principle of the “conservation of angular momentum” requires that rotation, like energy, cannot entirely disappear. Its total amount is conserved, so that when a nebula breaks up into stars, the original rotation of the nebula must be conserved in the rotations of the stars. Thus the stars, as soon as they come into being, are endowed with rotations transmitted to them by their parent nebula, in addition to the rotations resulting from the currents set up in the process of condensation.
Their continual loss of weight causes the physical conditions of the stars to change, and we shall find in the next chapter that this change generally involves a shrinkage of the star’s diameter. The same principle of “conservation of angular momentum” now requires that, as a star shrinks, its speed of rotation shall increase. In brief, as a star ages, it spins faster and faster.
[ p. 218 ] Now rotation was the essential factor in the birth of the stars out of the parent nebula. A nebula perfectly devoid of rotation would not, so far as we can see, break up into stars at all, and this prediction of theory appears to be confirmed by observation, since nebulae of the perfectly spherical type shewn in fig. 1 of Plate XVI can never be resolved into stars in the telescope. On the other hand we saw how nebulae which were initially endowed with rotation would continually increase their speed of rotation under shrinkage, until finally their rotation broke them up and produced a family of stars out of each. The question now obviously arises whether, as the speed of rotation of the stars increases, these are likely to break up in their turn, and produce yet a third generation of astronomical bodies. Again we might expect that mathematical analysis would apply to large and small bodies equally, irrespective of scale. And a detailed examination of the problem shews that in actual fact the process we have had under consideration would repeat itself, and again bring a further generation of smaller bodies into being, provided the physical conditions were suitable.
The physical conditions, however, prove not to be suitable; they certainly fail in one respect at least. Although a rotating star may eject gaseous matter in its equatorial plane, the whole process will be on a much smaller scale than in the nebulae. We might expect the ejected matter to form condensations as before, but calculation shews that, unless the molecular velocity is extraordinarily low, no condensation can survive unless it has a weight greater than the whole weight of the star ! This means that with any reasonable molecular velocity, the ejected gas would not [ p. 219 ] form condensations at all. It would merely scatter into the surrounding space, forming an atmosphere without any distinct condensations.
Such is the course of events if the stars, like the nebulae before them, are treated as pure masses of gas. Another alternative must, however, be considered.
The fission of liquid stars. We have seen how a gaseous nebula devoid of rotation would assume a strictly spherical shape under its own gravitational attraction, while slight rotation would cause it to flatten into an orange shape, like the earth. The earth also has assumed this shape on account of its rotation, although its internal structure is very different from that of a gaseous nebula.
Strict mathematical investigation shews that this flattened-orange shape must be common to all slowly rotating bodies, regardless of their internal composition ; gases, liquids, and plastic bodies assume it equally. But the shape of a rapidly rotating body must depend very greatly on its internal arrangement and constitution, being especially affected by the extent to which the weight of the body is concentrated near its centre.
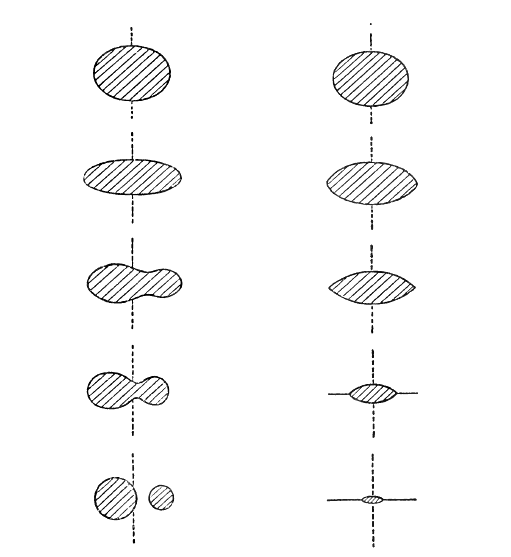
As a consequence of the high compressibility of gases, this central concentration of weight reaches its extreme limit in a purely gaseous mass. The opposite extreme is reached in a mass of uniform incompressible liquid such as water, in which there can be no central concentration at all. As a mass of this latter type increases its speed of rotation, the slightly flattened-orange shape merely gives place to the shape of a more flattened orange. The tendency of a gaseous mass to form a sharp edge round the equator is entirely absent, and the cross-section of its figure remains [ p. 220 ] elliptical throughout. At a still higher speed of rotation, the equator loses its circular shape and it too becomes elliptical. The figure has now three unequal diameters, but every cross-section is strictly elliptical; the figure is an “ellipsoid.” After this, its longest diameter begins to elongate until the mass, still ellipsoidal in shape, has formed a cigar-shaped figure with a length nearly three times its shortest diameter.
A new series of events now begins. The mass of liquid gradually concentrates about two distinct points on its longest diameter, a waist or furrow forming across its middle. This furrow gets deeper and deeper until it has cut the body into two distinct detached masses, which now rotate in orbital motion about one another and form a binary star. The sequence of events is shewn in fig. 11 ; diagrams of the final stage as represented by actual binary stars have already been given on p. 54.
For comparison the sequence of shapes assumed by a rotating mass of gas is shewn in fig. 12, this being identical with the sequence of observed nebular shapes which is actually observed, and is illustrated photographically in Plate XVI (p. 207).
The two chains of configurations shewn in figs. 11 and 12 represent, it will be remembered, the two extreme cases of a rotating body whose substance is distributed with complete uniformity, and of a rotating body whose substance is very highly condensed towards its centre. As the constitutions of actual astronomical bodies must lie somewhere between these two extremes, we might naturally expect such a body to follow a series of configurations intermediate between the two shewn in figs. 11 and 12. Theory shews that as a matter of fact it does not. All bodies having less than a certain [ p. 221 ] critical degree of central condensation follow the sequence shewn in fig. 11, or a sequence differing only immaterially from this; all bodies having more than this critical amount of central condensation follow the sequence shewn in fig. 12. Thus when this critical degree of central condensation is reached there is a [ p. 222 ] sudden swing over from fig. 11 to fig. 12. In brief, every rotating body conducts itself either as if it were purely liquid, or as if it were purely gaseous ; there are no intermediate possibilities.
Observational astronomy leaves no room for doubt that a great number of stars, possibly even all stars, follow the sequence shewn in fig. 11. No other mechanism, so far as we know, is available for the formation of the numerous spectroscopic binary systems, in which two constituents describe small orbits about one another. In these stars, then, the central condensation of mass must be below the critical amount just mentioned; to this extent they behave like liquids rather than gases.
We have relied entirely on mathematical analysis in tracing out the details of the process of fission just described. And we are totally unable to check our theoretical results by observation. There is not a single star in the sky of which we can say: here is a star which has certainly started to break up by fission, and will certainly end as a binary system. It is perhaps not altogether surprising. The breaking-up process is in all probability of very short duration by comparison with the lives of the stars, so that in any case we should have to investigate a great many stars before catching one in the act of breaking into two.
On the other hand, a star in the act of breaking up ought to be very easily differentiated from ordinary stars. Mathematical analysis shews that its interior would be in a state of considerable turmoil, so that it would hardly be likely to shine with a steady light: it would be a “variable” star. Further, its condition ought to shew a progressive change, although it is an open question whether this would be rapid enough to [ p. 223 ] be detected in a few years of observation. Finally, if any group or class of stars were suspected of being stars in process of fission, it ought to be possible to arrange them in an order corresponding to the extent to which the fissional process had advanced, and the sequence so formed ought to end with stars in the physical condition of newly formed binaries.
I have recently suggested that the Cepheid variables, whose unknown mechanism of light-variation renders such valuable service to the astronomer, are merely stars in the act of fission. Want of space prevents our entering here into the intricate question of how far they exhibit the peculiarities which mathematical analysis requires of stars in process of fission, but it is easily seen that they satisfy the three simple tests outlined above. They are certainly variable stars, and the light- variations of different stars are so similar as to suggest very strongly that they all arise from the same cause. The periods of a number of Cepheids are suspected of change, and Hertzsprung has estimated that the prototype star, δ Cephei, which has now been observed for 126 years, is decreasing its period of light-fluctuation at the rate of about a tenth of a second per annum; thus a million years would reduce its present period of 5⅓ days by over a day. Finally Dr Otto Struve has found that the sequence of Cepheids fits almost perfectly on to that of newly formed binaries. Thus the prospects for the “fission theory” of Cepheid variables seem hopeful, but the theory must be very thoroughly tested before it can be accepted, and it cannot be claimed that it has been so far either tested thoroughly or accepted extensively.
An alternative view, first propounded by Plummer and Shapley, regards Cepheid variables as pulsating [ p. 224 ] spheres of gas. The behaviour of such masses of gas has been investigated mathematically by Eddington and others, but it does not appear that it can be reconciled with the observed behaviour of Cepheid variables.
¶ The Development Of Binary Systems
Whatever the process of formation of binary systems may be, we experience fairly plain sailing in attempting to trace out the subsequent development of such systems. Three factors are simultaneously in operation.
Tidal friction. The first of these three factors, which is only of brief duration, was designated “tidal friction” by Sir George Darwin, who first drew attention to it, and investigated the manner of its operation. When first a rotating mass breaks up and forms a binary system, the two components are so near that they necessarily raise tremendous tides on one another; Darwin shewed that these drive the two bodies apart, and equalise their rates of rotation in so doing. After these processes have been in operation for millions of years, the rates of rotation of the two bodies and their rate of revolution about one another must all become equal, so that each body perpetually turns the same face to its companion, and the two rotate about one another like the two masses of a dumb-bell joined by an invisible arm.
Although a sun and planet do not form a binary system in the strict technical sense, they are necessarily subject to the same forces as true binary systems. Thus we can see the operation of tidal friction in the fact that Mercury always turns the same face to the sun, and that Venus rotates so slowly on its axis that [ p. 225 ] it turns the same face to the sun day after day, and probably also week after week. As we pass further out into space the effects of tidal friction rapidly diminish, but it is probably significant that the nearer planets, Earth and Mars, have days of about 24 hours each, while the remote planets Jupiter, Saturn and Uranus each have days of only about 10 hours. The periods of rotation of Neptune and Pluto are unknown. Apart from these we find, in a general way, that the further we recede from the sun the more rapidly the planets rotate, which is precisely the effect that ought to be produced by tidal friction.
In the same way, tidal friction has in all probability been mainly responsible for the present configuration of the earth-moon system, driving the moon away to its present distance from the earth and causing it always to turn the same face towards us. Tidal friction must of course still be in operation. The moon is responsible for the greater part of the tides raised in the oceans of the earth; these, exerting a pull on the solid earth underneath, slow down its speed of rotation, with the result that the day is continually lengthening, and will continue to do so until the earth and moon are rotating and revolving in complete unison. When, if ever, that time arrives, the earth will continually turn the same face to the moon, so that the inhabitants of one of the hemispheres of the earth will never see the moon at all, while the other side will be lighted by it every night. By this time the length of the day and the month will be identical, each being equal to about 47 of our present days. Jeffreys has calculated that this state of things is likely to be attained after about 50,000 million years.
After this, tidal friction will no longer operate in the [ p. 226 ] sense of driving the moon further away from the earth. The joint effect of solar and lunar tides will be to slow down the earth’s rotation still further, the moon at the same time gradually lessening its distance from the earth. When it has finally, after unthinkable ages, been dragged down to within about 12,000 miles of the earth, the tides raised by the earth in the solid body of the moon will shatter the latter into fragments (p. 250 below), which will form a system of tiny satellites revolving around the earth in the same way as the particles of Saturn’s rings revolve around Saturn, or as the asteroids revolve around the sun.
We have already noticed how the present arrangement of the earth-moon system enables us to calculate the earth’s age; Jeffreys estimates that the system must have taken something of the order of 4000 million years to reach its present configuration (p. 155).
This period, which seems so long when judged by terrestrial standards, is only a moment in the life of a star. The components of the true binary star attain a configuration like that of the earth-moon system in a brief fraction of their lives, and, passing on, reach in time the configuration in which each perpetually turns the same face to the other. Up to now, tidal friction has been driving the masses ever further apart, but as soon as this stage is attained, the tides become stationary on both components, so that tidal friction goes out of operation. Thus the separation produced by tidal friction has now reached its limit, and, so far as tidal friction is concerned, the two bodies might rotate in the way just described to all eternity.
Loss of weight. As tidal friction becomes inoperative, a new agency takes hold. We have calculated that the sun is losing weight at the rate of [ p. 227 ] 250 million tons a minute, that it has been losing weight at this rate, or some comparable rate, for millions of millions of years, and will continue so to do for millions of millions of years yet to come. The earth is at its present distance from the sun because this distance is exactly suited to the present weight of the sun. If the sun’s weight were suddenly reduced to half, its gravitational pull on the earth would also be reduced to half, and the earth would move to a greater distance from the sun[3].
The sun’s weight is not likely to be suddenly reduced to half, but it has been reduced by a thousand million tons in the last four minutes, with the result that its gravitational grip on the earth has been weakened and the earth has moved out to a wider orbit; at this moment the radius of the earth’s orbit is greater than it was four minutes ago. The details can be traced out mathematically with complete precision. It appears that the earth’s orbit round the sun is not a circle, or even an ellipse of small eccentricity; it is a spiral curve, like an uncoiled watch spring. Every year the earth moves a tiny step further out into the outer cold and darkness; exact calculation shews that its average distance from the sun increases at the rate of about a metre (39.37 inches) a century. The effect is of course of precisely the same kind as we have seen must be produced in the galactic system by the loss of weight of the stars. The only difference is that in the galaxy a system of thousands of millions of stars is expanding, whereas the sun-earth system consists of only two members.
[ p. 228 ] Precisely similar effects must be produced by the loss of weight in the two components of a binary star. Here both components are radiating away energy, and so are simultaneously losing weight. Detailed calculation shews that they must continually recede from one another, but that the shape of their orbit will undergo no change.
Neither separately nor in combination do the two effects just described explain either the shapes or the sizes of the observed orbits of binary stars as a whole. To interpret these we must call on yet a third agency, the gravitational forces from passing stars. We have already seen how these account for the statistical distribution of orbits which is actually observed.
The combination of all three agencies, tidal friction, extending over millions of years, loss of weight, extending over millions of millions of years, and disturbance from passing stars, extending over a similar period, is responsible for the evolution of binary star systems. Their aggregate effect is to widen the distance between the two stars, while at the same time knocking the orbit out of shape.
Subdivision. While these changes are going on in the orbital arrangement of a binary system, the two components are themselves changing their physical condition on account of their continual loss of weight, and, as with the parent stars, this loss of weight will generally result in a shrinkage in the size of the star. The shrinkage of either component of the system causes its shape to run through the sequence of configurations we have already enumerated, and if the shrinkage continues for long enough, the component may end by further dividing into two separate masses. [ p. 229 ] Either or both of the constituents of a binary system may subdivide into binary sub-systems in this way, resulting in a system of either three or four stars. H. N. Russell has shewn mathematically that when a binary system P, Q divides into a triple system, P, q, q’, through Q breaking up into two constituents q, q’, the distance between q and q’ cannot be more than about a fifth of the original distance PQ. This theoretical law is well confirmed by observation. Fig. 13 shews a typical multiple system, and we notice that the separations in each of the various sub-systems are all quite small in comparison with those of the main systems.

The development of the hypothetical primitive chaos has now been traced through five generations of astronomical bodies,
chaos — nebulae — stars — binary systems — sub-systems,
to which a sixth generation must be added if the stars of the sub-system happen to fission further, as, for instance, they have done in the star shewn in fig. 13. The genealogy of the stars begins with a vast tenuous nebula filling all space; the last generation consists of small, shrunken, dying stars with no capacity for further subdivision. The genealogy has been traced out primarily on theoretical grounds alone, but we need have no doubts as to its general accuracy, since observation confirms it repeatedly and at almost every step. Indeed it is hardly too much to say that the evolutionary sequence could have been discovered [ p. 230 ] almost equally well from observational evidence alone, except for the hypothetical primaeval chaos, about which, from the nature of the case, observation cannot have anything to say.
¶ The Origin Of The Solar System
Almost all observed astronomical formations can be placed in the evolutionary sequence we have just discussed, either with fair certainty or with reasonable plausibility, except for one outstanding and conspicuous exception — the Solar System. Cosmogony came into being as an attempt to discover the origin of the solar system. The reasons why it limited its efforts to this particular problem are chronological; in the early days of cosmogony, astronomy was barely conscious of anything outside the solar system. The sketch just given of the findings of modern scientific cosmogony has been remarkable in that it has exhibited cosmogony taking us a tour round the whole universe, explaining the origin and life-history of practically every object we encounter on this tour, and then becoming speechless when it is brought back home and confronted with its birthplace, the solar system.
Laplace’s nebular hypothesis. The first serious scientific cosmogony was that embodied in the famous Nebular Hypothesis of Laplace. In 1755 Kant had pictured a primaeval chaos condensing into spinning nebulae, and, identifying one of these nebulae with the sun, had imagined the planets to be formed by the solidification of masses of gas shed from the nebula, much in the way in which we have supposed the stars to be born. In 1796, Laplace advanced similar ideas, which he developed in detail with a mathematical [ p. 231 ] precision quite beyond the capacities of Kant. He shewed how, as its shrinkage made it spin ever faster and faster, a rotating mass of gas would flatten out, develop the lenticular form we have already discussed (fig. 3 of Plate XVI), and then proceed to eject matter in its equatorial plane, or rather to leave it behind as the shrinkage of the main mass continued. At this stage it would look somewhat like the nebulae shewn in figs. 4 and 5 of Plate XVI, although Laplace, being unacquainted with nebulae of this type, adduced Saturn surrounded by its rings as an example of the formation to be expected at this stage (Plate XXIV, p. 250). Laplace imagined that the fringe of abandoned gas would then condense and form a single planet. As the main mass shrunk further, more gas was abandoned in the equatorial plane, which in due course condensed into another planet, and so on, until the sun left off shrinking and no more planets were born. A repetition of the same process, but on a far smaller scale, resulted in the satellites being born out of the planets.
That the hypothesis is prima facie plausible, is evident from its having survived, and indeed been generally accepted, for nearly a century before it encountered any serious opposition. Recently criticisms have accumulated, of so vital a nature as to make it clear that the hypothesis must be abandoned.
The sun, according to Laplace, broke up and gave birth to planets through excess of rotation. Yet both theory and observation indicate quite clearly the fate in store for a star which rotates too fast for safety; it does not found a family, but merely bursts, like an overdriven fly-wheel, into parts of nearly equal size. Spectroscopic binary and multiple systems are the relics of stars which have broken up through excess of [ p. 232 ] rotation, and they do not in the least resemble the solar system.
Again, the principle of “conservation of angular momentum ” requires that the rotation of the primaeval sun shall persist in the rotation of the present sun, and in the revolutions of the planets around it. On adding together the contributions from all of these, we obtain a total which ought to represent the angular momentum of the primaeval sun. In strictness a further contribution ought to be added on account of the weight of all the radiation which the sun has emitted since the planets were born. We can calculate the amount of this contribution, because we know the age of the earth with tolerable accuracy, but it proves to be entirely negligible.
The total angular momentum of the primaeval sun can be calculated with very fair accuracy, because more than 95 per cent, of the total angular momentum of the present solar system resides in the orbital motion of Jupiter. This contribution can be calculated with great exactness, so that some uncertainty in the minor contributions which make up the remaining 5 per cent, can have but little influence on the total.
When this total is calculated the startling fact emerges that the primaeval sun cannot have had enough rotation to cause break-up at all. Clearly the sun is very far from being broken up by its present rotation. Flattening of figure is the first step towards break-up, and the sun’s figure is so little flattened by its present rotation that the most refined measurements have so far failed to detect any flattening at all. On adding the further angular momentum now represented in the motions of Jupiter and all the other members of the solar system, we arrive at a primaeval sun rotating [ p. 233 ] about as fast as Jupiter now rotates, and shewing about the same degree of flattening of figure as Jupiter — enough to measure quite easily in a telescope, or even to detect with the eye alone, but nothing like enough to cause break-up.
The sun is hardly likely to have altered much since its planets were born, for the intervening 2000 million years or so represent but a minute fraction of the sun’s total life. If, however, we imagine it to have shrunk appreciably in the interval, then the available amount of angular momentum would have been even more unable to break up the large primaeval sun than it is to break up the present shrunken sun. Whichever way we look at it, we reach the conclusion that the sun cannot have broken up, as Laplace imagined, through excess of rotation; indeed it can never have possessed more than a quite tiny fraction of the amount of rotation needed to break it up.
A third objection is of a somewhat different character. Laplace was a very great mathematician, and there was nothing the matter with his abstract mathematical theory, so far as it went. More refined modern analysis has confirmed it at every step, and observation does the same, as photographs of rotating nebulae (Plate XVI) bear witness. These photographs exhibit a process taking place before our eyes, which is essentially identical with that imagined by Laplace, except for a colossal difference of scale. Everything happens qualitatively as Laplace imagined, but on a scale incomparably grander than he ever dreamed of. In these photographs the primitive nebula is not a single sun in the making, but contains substance sufficient to form hundreds of millions of suns; the condensations do not form puny planets of the size of our earth, but [ p. 234 ] are themselves suns ; they are not eight or so in number, but must be counted in millions.
We may ask why the same thing cannot happen on the smaller scale imagined by Laplace — for are not the conclusions of mathematics applicable independently of the size of the body with which we are dealing? The answer has in effect been given already (p. 218). Everything happens on the smaller scale according to plan until we come to the formation of the condensations; here the question of scale proves to be vital. We have seen (p. 196) how the molecules which form the sun have condensed into a star because of their great number; the molecules in a room do not condense into anything at all because they are too few. In the same way, the molecules left behind by the slow shrinkage of a sun (assuming this for the moment to rotate rapidly enough to leave molecules behind) would not condense, because at any instant there would be too few of them available for condensation. They would be shed by driblets, and a driblet of gas does not condense but scatters into space. A mathematical calculation decides the question definitely, and the decision is entirely adverse to the hypothesis of Laplace. Apart from minor details, the process imagined by Laplace explains the birth of suns out of nebulae; it cannot explain the birth of planets out of suns.
Second body theories. Laplace imagined his sun to be alone in space, even its nearest neighbours being too remote to influence it in any way. It was the natural supposition to make; we have already remarked how exceedingly rare an event it must be for two stars to approach near enough to influence one another. Yet no possible mode of evolution of a star which remains alone in space seems able to explain the [ p. 235 ] origin of the solar system. As far back as 1750, Buff on had suggested that the solar system might have been produced through the disruption of the sun by another body, which he described as a “comet.” In propounding his Nebular Hypothesis, Laplace mentioned Buffon’s idea, but dismissed it somewhat curtly on the grounds that it seemed unable to account for the nearly circular orbits of the planets — an ill-founded objection, as we shall soon see. Yet when we find that a single star cannot of itself give birth to a solar system, it becomes natural to investigate what happens on the rare occasions on which the evolution of a star is directed along other paths by the near approach of a second star.
In 1880, Bickerton of New Zealand, reviving Buffon’s idea, supposed that the solar system had been formed by the collision of the sun with another star. He imagined the debris of the collision to form a third nebulous body, condensations in which formed the planets. He shewed how the resistance which the planets would encounter as they moved through the surrounding nebula would gradually make their orbits more circular, and so account for their present nearly circular shapes. Ten years earlier, the English writer, R. A. Proctor, had advanced similar ideas, although with less precision. In 1905 Professors Chamberlin and Moulton of Chicago advanced a modification of the same ideas, under the name of the “Planetesimal Hypothesis.” Discarding the idea of material collision, they supposed that a passing star exerted a powerful tidal pull on the sun, with the result that the ordinary solar prominences temporarily attained an extraordinary violence; the ejected matter was supposed to rise to unusual heights and condense into small solid bodies, the “planetesimals,” out of the aggregation of [ p. 236 ] which the planets were ultimately formed. These various theories were all purely speculative. They have shewn very little capacity either for surviving the acid test of mathematical analysis, or for explaining the more salient features of the solar system ; none of them, for instance, explains why the larger planets in the solar system are accompanied by families of satellites.
Three years before Chamberlin and Moulton advanced their planetesimal theory, I had speculated as to the possibility of tidal forces breaking up a star, and generating a solar system. In 1916, I investigated mathematically what would actually happen when one star raised violent tidal forces on another. The results I obtained seemed to me to demolish the planetesimal theory of Chamberlin and Moulton, and led me to put forward the present-day “Tidal Theory,” which I believe a large proportion of astronomers now accept as giving the most probable origin of the solar system ; it can of course make no claim to finality or certainty.
Tidal theory. When two stars or other bodies pass close to one another without collision, the primary effect must be that each raises tides in the other. The closer the approach, the higher the tides in general, although something must depend also on the speed with which the bodies pass one another, because this determines the length of time during which they influence one another.
It is likely that the two spiral arms which give their name and characteristic appearance to the spiral nebulae may owe their inception to a somewhat similar tidal action. Conditions here are different in that the rotation of the nebulae in any case causes them to emit matter in their equatorial planes, so that even small tidal forces should then cause this matter to concentrate [ p. 237 ] in two symmetrical arms. Under stellar conditions a far closer approach is necessary to draw matter out from the star, and it is then most likely that there will be two unequal and dissimilar arms, or possibly only one arm.
If the approach is very close indeed, the tides may assume an entirely different aspect from the feeble tides which the sun and moon raise in our oceans ; they may take the exaggerated forms of high mountains of matter moving over the surface of the star. An even closer approach may transform these mountains into long arms of gas drawn out from the body of the star. If, as will generally be the case, the two stars are of unequal weights, the lesser will in general suffer more disturbance than the weightier.
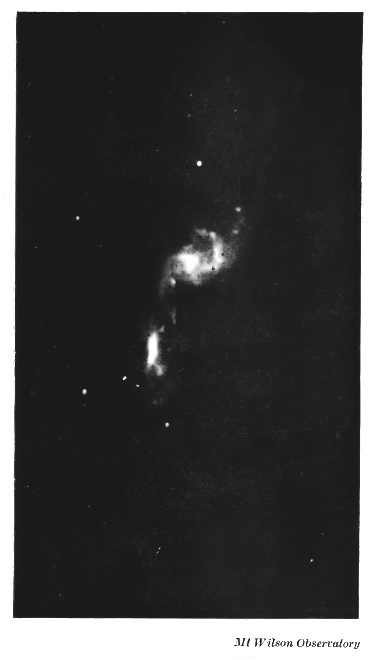
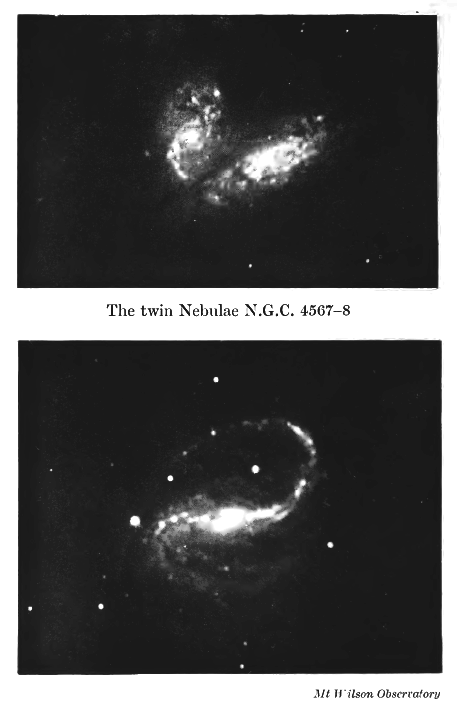
The birth of planets. The long arm or filament of matter drawn out of a star by tidal action is at first continuous in its structure, but analysis shews that it provides a fit subject for the operation of what we have called “Gravitational Instability.” Condensations begin to form in this long arm of gas, in the way already described. As before, the smaller condensations are dissipated, while the larger increase in intensity until finally the filament breaks up into a number of detached masses — planets have been born out of the smaller star. The pairs of nebulae shewn in Plate XXII and the upper half of Plate XXIII are very probably under one another’s tidal influence, and may serve to suggest the general nature of the process we are now considering, although it must be remembered that whatever is happening here is on an enormously greater scale than that of the solar system — if it were not, the telescope would be utterly unable to shew it to us.
When the new-born planets first begin to move as [ p. 238 ] separate and independent bodies, they are acted on by the gravitational pulls of both stars, and so describe highly complicated orbits. Gradually the bigger star recedes until its gravitational effect becomes negligible, and the planets are left describing orbits around the smaller star alone. If the planets moved in a clear field of empty space, these orbits would be exact ellipses. But the great cataclysm which has just occurred must have left all sorts of debris behind. Comets, meteors and other minor bodies which still survive in the solar system may represent a small part of it, but probably the main part was left in the form of dust or gas, so that the new-born planets had at first to plough their way through a medium which offered some resistance to their motions. Under these circumstances their orbits would not be strict ellipses. It can be proved that a resistance of the kind just described would change the shape of the orbits, and that with the progress of time they would become more circular, finally becoming absolutely circular if the medium should last long enough.
The debris of gas and dust would, however, continually be swept up by the planets and would disappear completely in time, probably leaving the planetary orbits something short of absolute circles. Assuming that all this has happened in the solar system, very little of the original debris can now remain, its last vestiges being probably represented by the particles of dust which are responsible for the zodiacal light. Nevertheless, the resisting medium appears to have existed for long enough to make the orbits, both of the planets and of their satellites, very nearly circular for the most part.
The exceptional cases are fully as significant as the [ p. 239 ] cases of conformity. Comparatively elongated orbits still exist in just those regions where we should expect the primaeval resisting medium to have been most sparsely spread in space, namely on the outermost confines of the solar system and of the various satellite system. Pluto, the outermost planet of all, has a more elongated orbit than any other planet. Again, in the systems of Jupiter and Saturn, the satellites with the most elongated orbits are those which are furthest away from their primaries. In addition to this, a general tendency may be discerned for elongated orbits to be associated with small weights, both in planets and their satellites. Mercury, with a weight of only a twentyfifth that of the earth, has a quite elongated orbit, as also to a less degree has Mars with a ninth of the weight of the earth. An explanation of this has been suggested by Jeffreys. Massive planets such as Jupiter and Saturn must have collected a large mass of the resisting medium round them, and carried it through space with them as a far-reaching envelope. The massive planets would have their motion checked by the interaction of the whole of this big envelope with the remainder of the medium, and so would attain circular orbits more rapidly than the lighter planets which had accumulated envelopes of very much smaller dimensions. And the same, with the appropriate modifications, is true of the satellite systems.
Jeffreys has calculated the rate at which planetary orbits would change their shape under the action of this resisting medium. The data of the problem are necessarily uncertain, and this uncertainty naturally affects his conclusions, but his study has yielded a valuable confirmation of other estimates of the length of time which has elapsed since the planets were born.
[ p. 240 ] We may next turn our attention to the physical changes which must all this time be affecting the various planets. The long filament of matter pulled out of the sun is likely to have been richest in matter in its middle parts, these parts having been pulled out when the second star was nearest and its gravitational pull was strongest. Diagrammatically at least, we may think of this filament as shaped like a cigar — thick near the middle, thin at the ends — so that when condensations begin to form, those near the middle are likely to be richer in matter than those at the ends. This probably explains why the two most massive planets, Jupiter and Saturn, occupy the middle positions in the sequence of planets.
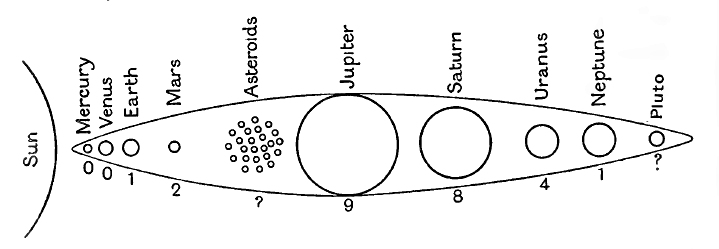
Fig. 14 shews the planets arranged in the order of their distances from the sun, with their sizes drawn roughly to scale. The thousands of asteroids whose orbits now fill the space between the orbits of Mars and Jupiter are represented as a single planet, it being generally supposed that these asteroids were formed by the break-up of what was originally a single planed in a way we shall shortly describe.
If we surround the planets by a continuous outline, as in the diagram, we can reconstruct in imagination [ p. 241 ] the cigar-shaped filament out of which they were produced, and we see at once how the biggest planets were produced where matter was most abundant.
The tidal theory which predicts all these features had been propounded, and its consequences worked out, many years before the new planet Pluto had been discovered. Valuable support for the theory may thus be found in the circumstance that Pluto behaves in every way according to the requirements of the tidal theory.
The birth of satellites. We have already noticed how the great disparity of weight between the sun and planets distinguishes the sun-planet formation from that of the normal binary star, and so suggests entirely different origins for the two formations. Exactly the same disparity repeats itself in the planet- satellite systems. Just as the parent sun is enormously more massive than its children the planets, so these in turn are far more massive than their satellite children. The sun has 1047 times the weight of its most massive planet and many millions of times the weight of the smallest. In the system of Saturn the corresponding figures are 4150 and about 16,000,000. The nearest approach to equality of weights is provided by the earth- moon system, the earth having only 81 times the weight of the moon. And, like the planetary system of the sun, the satellite systems of Saturn and, to a lesser degree, of Jupiter shew a general tendency for the weights of the various satellites to increase up to a maximum as we pass outwards from the planet, and then to decrease again. This again suggests formation out of a cigar- shaped filament with matter occurring most richly near the middle. In conjunction with the repetition of the great disparity of weights between primary and secondaries, this indicates very forcibly that the [ p. 242 ] satellites of the planets must have been born by the same type of process as had previously resulted in the birth of their parents.
We can imagine the process in a general way. Immediately after their birth, the planets must begin to cool down. The largest planets, Jupiter and Saturn, naturally cool most slowly and the smallest most rapidly. The latter may lose heat so speedily that they liquefy, and perhaps even solidify, almost immediately after their birth. While these events are in progress, the planets are still pursuing somewhat erratic orbits, in describing which they may pass so near to the sun that a second series of tidal disruptions occurs. In these the sun itself plays the role originally played by the passing star from space, the planets playing the part originally taken by the sun. The sun may now tear long filaments of matter out of the surfaces of the planets, and these, forming condensations, may give birth to yet another generation of astronomical bodies, the satellites of the planets. In some such way the tidal theory imagines the planetary satellites to have come into being.
Mathematical investigation shews that the more liquid a planet was at birth, the less likely it would be to be broken up by the still gaseous sun. If, however, such a break-up occurred, the weights of primary and satellites would be more nearly equal than if the planet had been more gaseous. Thus, on passing from wholly gaseous planets to planets which liquefied at or immediately after their birth, we should expect at first to find planets with large numbers of relatively small satellites, and then, after passing through the border-line cases of planets with small numbers of relatively large satellites, we should expect to come to planets having no satellites at all.
[ p. 243 ] We have already seen that the big central planets, Jupiter and Saturn, ought to have remained gaseous for longest and the smaller planets to have liquefied earliest; we now see that this prediction of theory exactly describes what is actually found in the solar system. Starting from Jupiter and Saturn, each with nine relatively small satellites, we pass Mars with only two satellites, and come to the earth with its one relatively large satellite, followed by Venus and Mercury which have no satellites at all. Proceeding in the other direction we leave Jupiter and Saturn each with their nine tiny satellites, to discover Uranus with four small satellites and Neptune with one comparatively big satellite. The number placed under each planet in fig. 14 gives the number of its satellites. When the numbers are exhibited in this way, the law and order in the arrangement of the satellite systems becomes very apparent, and this arrangement is seen to be exactly in accordance with the prediction of the tidal theory. The cigar-shaped arrangement applies not only to the sizes of the planets, but also, as it ought, to the numbers of their satellites.
The earth and Neptune, with only one satellite each, and those comparatively large ones, form the obvious lines of demarcation between planets which were originally liquid and those which were originally gaseous. This leads us to conjecture that Mercury, Venus and Pluto must have become liquid or solid immediately after birth, that the earth and Neptune were partly liquid and partly gaseous, and that Mars, Jupiter, Saturn and Uranus were born gaseous and remained gaseous at least until after the birth of their families of satellites.
We may perhaps find further evidence confirmatory [ p. 244 ] of the tidal theory in the circumstance that the weights of Mars and Uranus are abnormally small for their positions in the sequence of planets. If, as we have supposed, the planets were all born out of a continuous filament of matter, the weight of Mars at birth would in all probability have been intermediate between those of the earth and Jupiter, and the weight of Uranus intermediate between those of Neptune and Saturn. But if, as we have already been led to suppose, the two anomalous planets Mars and Uranus were the two smallest planets to be born in the gaseous state, they would be likely to lose more of their substance than the other planets through their outermost layers of molecules dissipating away into space before they had cooled down into the liquid state. If Mars and Uranus are supposed to be mere relics of planets which were initially far more massive than they now are, the anomalies begin to disappear and the pieces of the puzzle to fit together in a very satisfactory manner.
Orbital planes. Every rotating mass, whether gaseous, liquid or solid, has a definite axis of rotation, and, perpendicular to this, a definite equatorial plane which divides the mass symmetrically into two exactly equal and similar halves. When a mass breaks up under its own rotation, the equatorial plane and the symmetry still persist. Illustrations of this can be found in any set of photographs of rotating nebulae, as, for instance, those shewn in Plates XV and XVI. In more humble life an illustration is provided by the splashes of mud thrown off by a spinning bicycle- wheel, which all keep in the plane in which the wheel is spinning.
If the sun’s equatorial plane had proved to be a [ p. 245 ] plane of symmetry for the solar system, so that the whole system was similarly arranged as regards the two sides of this plane, it might have been possible to explain the system as the result of a rotational breakup. But the sun’s equatorial plane is not a plane of symmetry. The planets do not move in it, most of them moving in a plane which makes an angle of 5 or 6 degrees with it. In terms of our humble analogy, the splashes of mud are not flying about in the plane in which the bicycle-wheel is spinning.
The hypothesis that the planets came into being through a rotational break-up of the sun fails completely before this fact, but the tidal theory provides a simple explanation of it at once. The sun is still rotating much as it was before the planets were born, and so retains its original equatorial plane. The quite different plane in, or very close to, which the planets are describing orbits must clearly be the plane in which the long tidal filament was originally drawn out by the passing star. Thus the plane in which the outer planets now move must record the position of the plane in which the two stars, the sun and the wandering star, the second parent of the sun’s family of children, described orbits about one another 2000 million years ago. It is the only clue the latter has left of his identity, and is of course far too slight to make identification possible after this long lapse of time.
To sum up, we have seen that the normal mechanism by which the greater part of the universe has been carved out is the birth of successive generations of astronomical bodies through the action of “gravitational instability.”
The normal genealogy runs somewhat as follows:
_chaos — nebulae — stars — binary systems — sub-systems. _
[ p. 246 ] Not all stars have passed on to the last two generations; where only a small amount of rotation was present, a star might well live its whole life without further subdivision. Our sun would have provided an instance of this had it not been for the rare accident of the close approach of a second star. From the interaction of these, two other generations came into being, still through the mechanism of gravitational instability. For our solar system, as for any other similar systems there may be in the sky, the genealogy runs as follows :
chaos — nebula — sun — planets — satellites.
Both types of genealogy shew five generations, each born from its parent through the action of gravitational instability, and between them the two genealogies include practically all the large-size astronomical objects with which we are acquainted. It is then fair to say that “gravitational instability” appears to be the agency primarily responsible for the main architecture of the universe.
Roche’s limit. The reign of gravitational instability must end with the birth of planetary satellites, since gaseous bodies of less weight than these could not hold together. Even under the most favourable circumstances their feeble gravitational pulls would be unable to restrain their outermost molecules from escaping, so that the whole mass would speedily scatter into space. Yet astronomy provides many instances of smaller bodies; we have already mentioned the asteroids, meteors or shooting-stars, and the particles of Saturn’s rings. As all these are too small to have been born in the gaseous state, we must suppose them to be the broken-up fragments of larger masses. This accords with the circumstance that these small [ p. 247 ] bodies as a rule do not occur individually but in swarms.
The asteroids occur as a single swarm. If these were found scattered throughout the solar system, their origin might present a difficult problem. As things are, the whole swarm can be explained quite simply as the broken fragments of a primaeval planet. Saturn’s rings again admit of a natural explanation as the fragments of a former shattered moon of Saturn. Comets, which we have hardly had occasion to mention so far, are in all probability swarms of minute bodies which are just held together sufficiently by their mutual gravitational attraction to describe a common orbit in space. At its apparition in 1909, Halley’s comet was estimated to reflect as much of the sun’s light as a single body 25 miles in diameter. Yet its apparent surface was 300,000 times that of such a body, and was quite transparent. It is difficult to resist the conclusion that the comet consisted of a widely-spaced swarm of small bodies, and such a swarm again admits of a simple explanation as the broken fragments of a single mass.
Shooting-stars, or meteors, also are encountered in swarms. As we shall see later, the motion of many of these swarms makes it possible to identify them as broken-up comets. Thus the broken fragments which compose a comet are identical with the meteors which we see as shooting-stars when they penetrate into the earth’s atmosphere. Shapley has estimated that the earth’s atmosphere must catch thousands of millions of shooting-stars every day, of which at most only one in a hundred is bright enough to be visible to the naked eye. Generally they dissolve into vapour before they reach the earth’s surface (see p. 176); occasionally one [ p. 248 ] is so big that the earth’s atmosphere fails to dissipate it entirely, and what remains of it strikes the earth as a solid body — a meteorite. Every shooting-star and meteorite may be regarded as a miniature comet, consisting of only a single fragment. On occasions a whole group of fragments, moving in parallel paths at only small distances apart, may strike the earth’s atmosphere and appear as a “fireball.” Generally speaking all the small fry of the solar system move in swarms, and can be naturally interpreted as the broken-up fragments of larger bodies.
If the meteorites are broken fragments of bodies which were born out of the sun at the same time as the planets, they must have solidified at about the same time as the earth, at an epoch which we have placed at about 2000 million years ago. But if they had been born out of some other star, the time of their solidification might have been anywhere up to millions of millions of years ago.
Professor Paneth and two colleagues at Konigsberg have recently estimated the ages of various meteoric stones by methods similar to those employed to fix the age of the earth (p. 154). They obtain ages which range from a few million years up to 2900 million years, but there is nothing beyond this last figure. Not a single stone suggests an age even approaching millions of millions of years. This provides very strong evidence that these stones were products of the same cataclysm as produced the earth, and incidentally provides valuable confirmation of our previous estimate of the earth’s age.
We can easily see how larger bodies might be broken up into swarms of meteors. We have supposed the sun to have been broken up, at least to the extent of ejecting [ p. 249 ] a family of planets, by the tidal pull of a passing star. What would have happened if the passing star had not passed, but had eome to stay? So long as it remained within a certain distance of the sun, its tidal forces were pulling the sun to pieces. We can imagine how a longer visit from it would have resulted in a greater upheaval in the sun, and the birth of a larger family of planets. Finally a visit of unlimited duration would have shattered the sun into fragments.
In 1850 Roche gave a mathematical investigation of this process of tidal break-up. His discussion dealt only with solid or liquid bodies, but the underlying mechanism is the same whether the bodies are solid, liquid or gaseous. We have seen that the smaller of the two bodies involved in a tidal encounter suffers the most. Roche dealt only with the case in which one body was very small in comparison with the other; in such a case the small body was completely broken up, while the larger one remained unscathed. Roche imagined the small body to describe an orbit of gradually decreasing size around the big body. If the two bodies were of equal density, he calculated that the small body would be broken up as soon as the radius of its orbit fell to 2.45 times the radius of the large body. If the bodies are of different density the matter is slightly more complicated. We must imagine the larger body to expand or contract until it has the same average density as the smaller body; the critical distance is then 2.45 radii of the larger body in its imaginary expanded or contracted state.
This distance is generally known as Roche’s limit. A satellite can with safety describe a circular orbit about its primary so long as this orbit lies beyond Roche’s limit, but it is broken into fragments as soon as [ p. 250 ] it trespasses within the limit. The following figures confirm Roche’s mathematical analysis:
| Radius | Value |
|---|---|
| Radius of Saturn’s outermost ring | 2.30 radii of Saturn |
| Roche’s limit | 2.45 radii of primary |
| Radius of orbit of Saturn’s innermost satellite | 3.11 radii of Saturn |
| Radius of orbit of Jupiter’s innermost satellite | 2.54 radii of Jupiter |
| Radius of orbit of Mars’ innermost satellite | 2.79 radii of Mars |
At the same time they suggest very forcibly that Saturn’s rings are the broken-up fragments of a former satellite which ventured into the danger-zone marked out by Roche’s limit. We have seen how our own moon is destined in time to contract its orbit, until it is finally drawn within the Roche’s limit surrounding the earth and broken into fragments. After this the earth will have no moon, but will be surrounded by rings like Saturn.
We speak of Saturn’s rings in the plural, because two distinct circular gaps cause an appearance of three detached riFngs. There is a tendency to jump to the hasty inference that the rings are the shattered remains of three distinct satellites, but it is not so. Goldsbrough has shewn how certain orbits around Saturn are rendered unstable by the motions of the larger satellites of Saturn, so that no particle could permanently remain in such an orbit. He has calculated positions for these unstable orbits, and these are found to agree exactly with the positions of the observed divisions between the rings. Thus Saturn’s rings were in all probability produced by the breakage of a single satellite. The ring of small satellites which our moon will ultimately form round the earth will contain no divisions, because the earth has no other moons to render certain orbits unstable.

[ p. 251 ] Roche’s fundamental idea can be extended in many directions and admits of varied applications. There must, for instance, be a danger-zone, marked off by a Roche’s limit, surrounding the sun. The distance of this danger-zone from the sun depends on the density of the body for which it is dangerous (p. 249). For a body having the low density of a comet the distance will be very great indeed. Whatever the distances of their danger-zones, comets must occasionally pass through them and become broken up in so doing. Two comets, Biela’s comet (1846) and Taylor’s comet (1916), were observed actually to break in two while at about the earth’s distance from the sun, and in 1882 a comet was seen to divide into four parts. Biela’s comet returned in due course (1852) in the form of two distinct comets a million and a half miles apart, since which time neither part of the original comet has been seen again. The orbit of this comet was identical with that of the Andromedid meteors, which make a display of shooting-stars in the earth’s atmosphere on favourable 27ths of November, so that it is likely that these shooting-stars are the broken remains of Biela’s comet. Other conspicuous swarms of shooting-stars also move in the tracks of comets — the Leonids which used to make a magnificent show every 33 years move in the track of Comet 1866 I, the Perseids in the track of another Comet (1862 II), and the Aquarids in the track of Halley’s famous comet. In each case, there can be little doubt that the shooting- stars are scattered fragments of the comets. Besides this there are several families of comets whose members follow one another round and round in the same orbit, as though they had originally formed a single mass.
In the same way a Roche’s limit must surround the planet Jupiter, so that comets and other bodies may [ p. 252 ] be broken up through getting inside the danger-zone marked off by this limit. Jupiter’s innermost satellite is already perilously near it. But the greatest interest of this particular danger-zone is that it probably accounts for the existence of the asteroids. In the early days of the solar system, when the orbits of the planets were less nearly circular than they now are, a primaeval planet between Mars and Jupiter may well have described an orbit so elongated as to take it repeatedly within the danger-zone of Jupiter. If so, we need look no further for the origin of the asteroids. It is significant that the average orbit of all the asteroids agrees almost exactly with that of the planet which Bode’s law (p. 19) would require to exist between Mars and Jupiter.
¶ Footnotes
This is near enough, but not absolutely accurate. Exact mathematical analysis shews that the weight of the minimum condensation M is given by
where C, γ, ρ, κ are the molecular velocity, gravitation constant, initial density, and ratio of specific heats, whereas the weight from which molecules moving with velocity C just fail to escape is given by
With $ \kappa = 1 \frac{2}{3}$ the minimum weight of condensation is 9.7 times the weight which is just adequate to retain the molecules. ↩︎
The following estimates have already been mentioned:
Weight of Galaxy in terms of sun: 240,000,000,000
„ nebula M 31 in terms of sun: 3,500,000,000
„ „ N.G.C. 4594 in terms of sun: 2,000,000,000 ↩︎Although the details are unimportant, the actual course of events would be that the earth would begin to describe an elliptic instead of a circular orbit about the sun, the earth’s average distance being greater than now. ↩︎