Author: Sir James Jeans, M. A., D. Sc., Sc. D., LL. D., F. R. S.
[ p. 253 ] The process of carving out the universe which we considered in the last chapter ends normally with a simple star, although special accidents may have other consequences. As the result of close approaches with other stars, a tiny fraction of the total number of the stars, perhaps about one star in 100,000 (p. 341 below), may be attended by a retinue of planets. Another fraction, still small, although far greater than the foregoing, appears to have broken up as the result of excessive rotation, and formed binary or perchance multiple systems. But the destiny of the majority of stars is to pursue their paths solitary through space, neither breaking up of themselves nor being broken up by other stars. The only contact such stars have with the outer universe is that they are incessantly pouring away radiation into space. This outpouring of radiation is almost entirely a one-way process, any radiation a star may receive from other stars being quite inappreciable in comparison with the amount it is itself emitting. The radiation is accompanied by a loss of weight, and this again is all give and no take, the weight of any stray matter the star may sweep up out of space, like that of any radiation it receives, being quite inappreciable in comparison with the weight it loses by radiation. Without unduly straining the facts, the normal object in the sky may be idealised as a solitary body, alone in endless space, which continually pours out radiation and receives nothing in return.
In the present chapter we shall consider the sequence [ p. 254 ] of changes which such a star may be expected to experience during the course of its life. Having already discussed the mechanical accidents to which stars are liable, namely, fission through rotation and break-up through the tidal action of a passing star, we now turn to consider the life of a normal star which escapes all accidents until it finally becomes extinct through mere old age.
It will be necessary in the first place to describe the physical states of the various types of stars observed in the sky, and as a preliminary to this we must explain how the observations of the astronomer are translated into a form which gives us direct information as to the condition of the star.
Surface-temperature. In Chapter II (p. 140) we saw how each colour of light or wave-length of radiation has a special temperature associated with it, light of this colour predominating when a body is heated up to the temperature in question. For instance, a body raised to what we call a red heat emits more red light than light of any other colour, and so looks red to the eye.
Thus if a star looks red, it is legitimate to infer that its surface is at the temperature we describe as a red heat. If another star has the colour of the carbon of an arc-light, we may conclude that its surface is at about the same temperature as the arc. In this way we can estimate the temperatures of the surfaces of the stars.
In practice the procedure is not so crude as the foregoing description might seem to imply. The astronomer passes the light from a star through a spectroscope, thus analysing it into its different colours. By a process of exact measurement, he then determines the [ p. 255 ] proportions in which the different colours of light occur. This shews at once which colour of light is most plentiful in the spectrum of the star. Either from this or from the general distribution of colours, he can deduce the temperature of the star’s surface.
We have already seen (p. 123) how Planck discovered the law according to which the radiation emitted by a full radiator is distributed amongst the different colours or wave-lengths of the spectrum. The four curves shewn in fig. 15 represent the theoretical distribution for the radiation emitted by surfaces at the four temperatures 3000, 4000, 5000 and 6000 degrees respectively. The different wave-lengths of light are represented by points on the horizontal axis, [ p. 256 ] the marked wave-lengths being measured in the unit of a hundred-millionth part of a centimetre, which is usually called an Angstrom. The height of the curve above such a point represents the abundance of radiation of the wave-length in question.
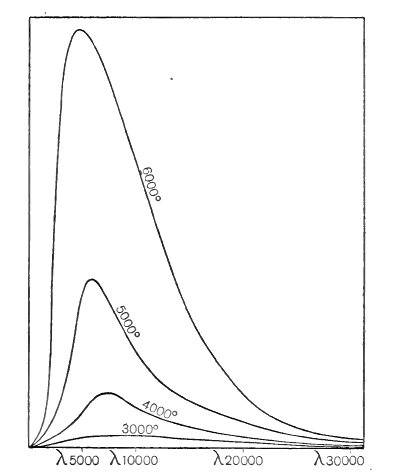
The two methods of determining stellar temperature will be easily understood by reference to these curves. The 6000 degrees curve reaches its greatest height at a wave-length of 4800 Angstroms, so that if light of wave-length 4800 Angstroms proves to be most abundant in the spectrum of any star, we know that the star’s surface has a temperature of 6000 degrees. The second method consists merely in examining to which of the theoretical curves shewn in fig. 15 the observed curve can be fitted most closely.
Either of these methods indicates that the temperature of the sun’s surface is about 6000 degrees absolute, which is nearly twice the temperature of the hottest part of the electric arc. The total amount of light and heat received on earth from the sun shews that the sun’s radiation must be very nearly, although not quite, the “full temperature radiation” (p. 123) of a body at this temperature. This is also shewn by the sun’s radiation being distributed among the various colours in a way which conforms very closely to the theoretical curve for a full radiator at 6000 degrees shewn in fig. 15.
The surface-temperature of a star can also be estimated from its spectral type. Many of the lines in stellar spectra are emitted by atoms from which one or more electrons have been torn off by the heat of the star’s atmosphere. We know the temperatures at which the electrons in question are first stripped off their atoms, and so can deduce the star’s temperature.
[ p. 257 ] The temperatures which correspond to the different types of stellar spectra as shewn in Plate VIII (p. 51), are approximately as follows :
| Spectral type | Temperature |
|---|---|
| B | 23,000 |
| A | 11,000 |
| F | 7,400 |
| G | 6,000 |
| K | 5,100 |
| M | 3,400 |
The last three entries in the table refer only to normal stars having diameters comparable with that of the sun. We shall find (p. 276) that a second class of stars (giants) exist, whose diameters are enormously greater than the sun’s. These have the substantially lower temperatures shewn below :
| Spectral type | Temperature |
|---|---|
| G | 5600 |
| K | 4200 |
| M | 3200 |
In studying stellar structure and mechanism, we are less concerned with the heat of the star’s surface as measured by its temperature, than with the amount of radiation it pours out per square inch.
This of course depends on the temperature; the hotter a surface, the more radiation it emits. But the temperature does not measure the quantity of radiation emitted. If we double the temperature of a surface it emits 16 times, not twice, its previous amount of radiation; the radiation from each square inch of surface varies as the fourth power of the temperature. [ p. 258 ] As a consequence, a star with a surface-temperature of 3000 degrees, or half that of the sun, emits only a sixteenth part as much radiation per square inch as the sun[1]. The radiation of each star is a compound of light, heat and ultra-violet radiation, and the proportions of these are not the same in different stars ; the cooler a star’s surface the greater the fraction of its radiation which is emitted as heat. Thus the star at 3000 degrees will emit nothing like as much as a sixteenth of the sun’s light per square inch, but will emit more than a sixteenth of the sun’s heat.
This shews that the total emission of radiation of a star cannot be estimated from its visual brightness alone; a substantial allowance must always be made for invisible radiations, both for the invisible heat at the red end of the spectrum and for the invisible ultra-violet radiation at the other end. The importance of these corrections is shewn in fig. 16. The four thick curves are identical with those already given in fig. 15, and shew how the radiation from a star of given surface- temperature is distributed over the different wave- lengths. The total radiation emitted at any temperature is of course represented by the whole area enclosed between the corresponding curve and the horizontal axis. The eye is only sensitive to radiation of wave- lengths lying between 3750 and 7500 Angstroms, so that of all this radiation only that part in the shaded strip is visible, all the rest representing invisible radiation.
We see at once that a fair proportion of the radiation emitted by a star at 6000 degrees comes within the range of visibility, but only a small fraction of that emitted by a star at 3000 degrees. Taking the stars [ p. 259 ] as a whole, star-light forms only a small part of the total radiation of the stars.
If our eyes were suddenly to become sensitive to all kinds of radiation, and not to visual light alone, the appearance of the sky would undergo a strange metamorphosis. The red stars Betelgeux and Antares, which are at present only 12th and 16th in order of brightness, would flash out as the two brightest stars in the sky, while Sirius, at present the brightest of all, would sink to third place. A star in the very undistinguished constellation of Hercules would be seen as the sixth brightest star in the sky. It is the star α Herculis, at present outshone by about 250 stars. As a consequence of its extremely low temperature of 2650 degrees, this [ p. 160 ] star emits its radiation almost entirely in the form of invisible heat. For instance it emits 60 times as much heat as the blue star η Aurigae, whose temperature is about 20,000 degrees, but only four-fifths as much light.
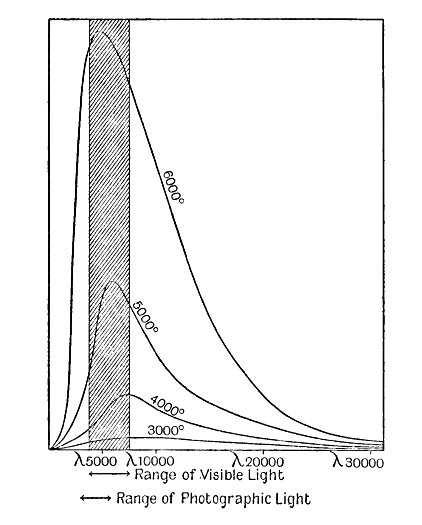
Allowances for invisible radiation have been made in all the calculations referred to in the present book, although it has not been thought necessary continually to restate this.
Stellar diameters. It is easy to measure the diameter of a planet, because this appears in the telescope as a disc of finite size. But the stars are too remote for their diameters to be measured in the same way. No star appears larger in the sky than a pin-head held at a distance of six miles, and no telescope yet built can shew an object of this size as a disc. All stars, even the nearest and largest, appear as mere points of light[2], so that their diameters can only be measured by roundabout methods.
When a star’s distance is known, we can tell its luminosity from its apparent brightness. From this, after allowing for invisible radiation, we can deduce the star’s total outpouring of energy — so many million million million million horse-power. We also know its outpouring of energy per square inch of surface, because this depends only on its surface- temperature which we deduce directly from spectroscopic observation. Knowing these two data, it is a mere matter of simple division to calculate the number of square inches which make up the star’s surface, and this immediately tells us the diameter of the star.
The diameters of exceptionally large stars may be [ p. 261 ] measured more directly by an instrument known as the interferometer. When we focus a telescope on a star we do not, strictly speaking, see only a point of light, but a point of light surrounded by a rather elaborate system of rings of alternating light and darkness, called a diffraction pattern. It might be thought that the size of these rings would tell us the size of the star, but the two have nothing to do with one another. The rings represent a mere instrumental defect, their size depending solely on the size and optical arrangement of the telescope. Following a method suggested by Fizeau in 1868, Professor Michelson has shewn how even this defect can be turned to useful ends, and by its aid has produced what is perhaps the most ingenious and sensational instrument in the service of modern astronomy — the interferometer. In effect, this instrument superposes two separate diffraction patterns of the same star, and sets one off against the other in such a way as to disclose the size of star producing them. The diameters of a few of the largest stars have been measured in this way, so that we may say that we know their sizes from direct observation. In every case the directly measured diameter agrees fairly well, although not perfectly, with that calculated indirectly in the way already explained. The discrepancies, which are not serious, appear to result from red stars not being accurate “full radiators ” in the sense explained on p. 123.
The interferometer method is only available for the largest stars, but at the extreme other end of the scale the theory of relativity has come to the rescue. Einstein shewed it to be a necessary consequence of his theory of relativity that the spectrum of a star should be shifted towards the red end by an amount [ p. 262 ] depending on both the weight and the diameter of the star. If, then, a star’s weight is known, the observed spectral shift ought immediately to tell us its diameter. This spectral shift has recently been observed in the light received from the companion of Sirius, and measurements of its amount lead to a value for the star’s diameter which agrees exactly with that calculated from its luminosity. Thus at both ends of the scale, for the very largest as well as for the very smallest of stars, direct observation confirms the values calculated for the diameters of the stars.
We may accordingly feel every confidence in the calculated diameters of all stars, even when these cannot be checked by direct measurement. Indeed a discrepancy between the true and calculated diameters could only arise in one way. The diameters are calculated on the assumption that the stars emit their full temperature-radiation. If the stars had been partially transparent like the nebulae, or solid bodies like the moon, this assumption would have been false, and its falsity would at once have been shewn by discordances between the calculated and measured diameters of the stars. The fact that no large discordances appear suggests that the stars emit nearly full temperature-radiation throughout the whole range of size from the largest to the smallest.
¶ The Variety Of Stars
Observation shews that the physical characteristics of the stars vary enormously, so that it is easy, as we shall soon see, to tell a sensational story by contrasting extremes, setting the brightest against the dimmest, the biggest against the smallest, and so on. This would, [ p. 263 ] however, give a very unfair impression of the inhabitants of the sky; it would be like judging a nation from the giants and dwarfs, the strong men and the fasting men, seen inside the showman’s tent.
We shall obtain a more balanced impression of the actual degree of diversity shewn by the stars as a whole if we consider the physical states of those stars which are nearest the sun. By taking these precisely in the order in which they come, we avoid any suspicion of going out of our way to introduce stars merely because they are bizarre or exceptional. The small group of stars obtained in this way may be expected to form a fair sample of the stars in the sky, although of course it will not be a large enough sample to include extremes. We need not discuss the sun itself in detail because it will figure as our standard star, with reference to which all comparisons are made.
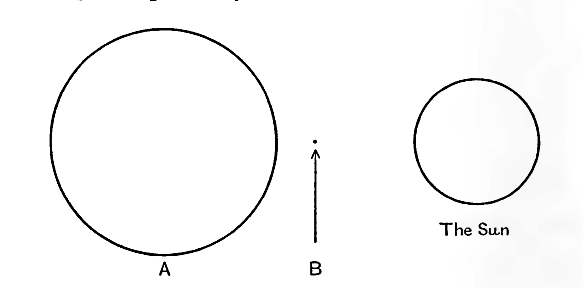
The System of α Centauri. This system consists of three constituent stars, which are believed to be our three nearest neighbours in space.
The brightest, α Centauri A, is very similar to the sun. It is of the same colour and spectral type, but weighs 14 per cent, more and is about 12 per cent, more luminous. Being of the same colour as the sun, it emits the same amount of radiation per square inch. Thus its 12 per cent, greater luminosity shews that it must have a surface 12 per cent, greater, and therefore a diameter 6 per cent, greater, than the sun.
The second constituent, α Centauri B, is considerably redder than the sun, its surface-temperature being only about 4400 degrees against the sun’s 6000 degrees or so. It has 97 per cent, of the sun’s weight, but only about a third of its luminosity. Yet, as a consequence of its low temperature, it needs 50 per cent, more [ p. 264 ] area than the sun to discharge a third of the sun’s radiation; this makes its diameter 22 per cent, greater than that of the sun. α Centauri A and α Centauri B together form a visual binary, the two components revolving about one another in a period of 79 years.
Neither of these two constituents is very dissimilar from the sun, but the third star of the system, Proxima Centauri, is of an altogether different type. It is red in colour, with a surface-temperature of only about 3000 degrees. It is exceedingly dim, emitting only a ten-thousandth part as much light as the sun, and has only a fourteenth part of the sun’s diameter. Its weight is unknown.
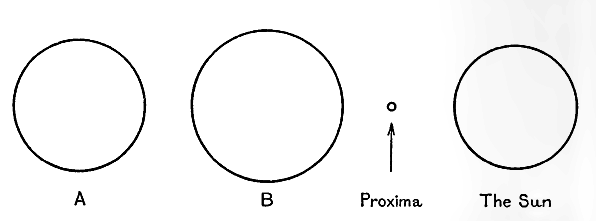
The sizes of the three stars of this system, with that of the sun for comparison, are shewn in fig. 17.
Munich 15040. This is a single faint star about which little is known. Its surface is red, with a temperature probably little above 2500 degrees, and it emits only th of the light of the sun.
Wolf 359. This is the faintest star yet discovered, but beyond this very little is known about it. It is red in colour and emits only about th the light of the sun.
[ p. 265 ] Lalande 21185. Another faint red star, emitting th of the light of the sun.
The System of Sirius. This consists of two very dissimilar stars, there being some suspicion that a third also may exist.
The principal star, Sirius A, which appears as the brightest star in the sky (the Dog-star), is white in colour and has a surface-temperature of about 11,000 degrees. As this is nearly twice the sun’s temperature, Sirius A emits nearly 16 times as much radiation per square inch as the sun. Its luminosity is about 26 times that of the sun, and this requires the star’s diameter to be 58 per cent, greater than that of the sun. It has nearly four times the sun’s volume, but only 2.45 times its weight, so that matter is not as closely packed in Sirius A as in the sun. An average cubic metre contains 1.42 ton in the sun, but only 0.93 ton in Sirius A.
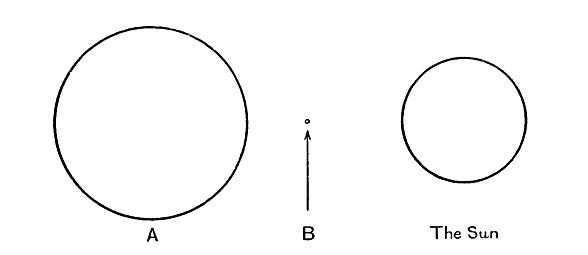
The faint companion Sirius B is one of the most interesting stars in the sky. It is of nearly the same colour and spectral type as Sirius A, but emits only a ten-thousandth part as much light. After allowing for the slight difference in surface- temperature, we find [ p. 266 ] that its surface is only th, and its diameter th of that of Sirius A. Yet Sirius A weighs only three times as much as Sirius B, although having 125,000 times its volume. It is not Sirius A but Sirius B that is remarkable; the average density of matter in the latter is about 60,000 times that of water, the average cubic inch containing nearly a ton of matter. Fig. 18 shews the sizes of the two components of Sirius drawn to the same scale as fig. 17.
B.D. 12° 4523 and Innes 11 h. 12 m., 57.2°. Two stars, as to the physical state of which nothing is known, except that they are very faint, emitting th and the sun’s light respectively.
Cordoba 5 h. 343 and τ Ceti. Two faint stars, both of reddish colour, emitting and a third of the sun’s light respectively.
The System of Procyon. This is a binary system, similar in many respects to Sirius. The main star, Procyon A, is of the same general type as the sun, but weighs 24 per cent, more, and emits 5½ times as [ p. 267 ] much light. Its surface-temperature is about 7000 degrees, and its diameter is 1.80 times that of the sun.
The faint companion, Procyon B, is so faint that nothing is known as to its physical condition except that it emits only th of the light of the sun. Its weight is 39 per cent, of the sun’s weight.
Fig. 19 shews the sizes of the two components of Procyon on the same scale as before.
Next in order, as we recede from the sun, come eight very undistinguished stars, every one of which is redder and fainter than the sun, none of them having a surface-temperature higher than 5000 degrees, and none of them emitting more than a quarter of the sun’s light. After these we come to
The System of Kruger 60. This is a binary system in which both components are small, red and dim.

The brighter component, Kruger 60 A, has a surface- temperature of 3200 degrees, and emits th of the light of the sun. Its diameter is a third, and its weight a quarter of the sun’s; so that its substance must be packed about 7 times as closely as that of the sun. The fainter component, Kruger 60 B, has a similar surface-temperature but emits only th of the sun’s light. Its diameter is a sixth, and its weight a fifth of [ p. 268 ] the sun’s; so that its substance must be packed about 40 times as closely as that of the sun. The system is illustrated in fig. 20.
van Maaneri’s star. Another very faint star, which has the high surface-temperature of 7000 degrees. Notwithstanding this, it only emits th of the sun’s light. Consequently its diameter is only about th of the sun’s, the star being if anything smaller than the earth. Its weight is unknown, but its substance is in all probability packed even more closely than in Sirius B.
The discussion of this sample of stars suggests that the majority of stars in space are smaller, cooler and fainter than the sun. Stars exist which are far brighter than the sun, but they are exceptional, the average star in the sky being a small dull dim affair in comparison with our sun.
With this sample of the average population of the sky before us, we may proceed to discuss the various characteristics of stars in a systematic way, without fearing to mention extremes. Let us begin with their weights.
Stellar weights. The two stars of smallest known weight in the whole sky are the faint constituent of Kruger 60, just discussed, and the faintest constituent of the triple system ο2 Eridani, each of which has a fifth of the sun’s weight. But the stars whose weights are known are so few that there can be no justification for supposing these to be the smallest weights which occur in the whole universe of stars. A general survey of the situation, on lines to be indicated later ([#p281]), suggests that there may be many stars of still smaller weight, but that very [ p. 269 ] few are likely to have weights which are enormously smaller. Probably very few stars weigh as little as a tenth of the sun’s weight.
The vast majority of stars have weights intermediate between this and ten times the sun’s weight. Stars which weigh even three times as much as the sun are rare, those which weigh ten times as much are very rare, probably only about one star in 100,000 having ten times the weight of the sun. Even higher weights undoubtedly occur — we have already mentioned Plaskett’s star, whose two constituents have more than 75 and 63 times the sun’s weight respectively, and the quadruple system 27 Canis Majoris which to all appearances weighs 940 times as much as the sun — but such instances are very, very unusual. We may say that as a general rule the weights of the stars lie within the range of from a tenth to ten times the sun’s weight, and we shall find that stars differ less in their weights than in most of their other physical characteristics.
Luminosity. A far greater range is shewn, for instance, in the luminosities of the stars — in their candle-powers measured in terms of the sun’s candle- power as unity. The most luminous star known is S Doradus, already mentioned, with 300,000 times the luminosity of the sun, while the least luminous is Wolf 359 with only a fifty-thousandth part of the luminosity of the sun. The range of stellar luminosities, as of stellar weights, extends about equally on the two sides of the sun, so that the sun is rather a medium star in respect both of weight and luminosity. It is medium in the sense of being about half-way between extremes, but we have seen that there are many more stars below than above it.
[ p. 270 ] In comparison with the very moderate range of stellar weights, the range of luminosity is enormous; S Doradus is 15,000,000,000 times as luminous as Wolf 359. If S Doradus is a lighthouse, Wolf 359 is something less than a firefly, the sun being an ordinary candle. If the sun suddenly started to emit as much light and heat as S Doradus, the temperature of the earth and everything on it would run up to about 7000 degrees, so that both we and the solid earth would disappear into a cloud of vapour. On the other hand, if the sun’s emission of light and heat were suddenly to sink to that of Wolf 359, people at the earth’s equator would find that their new sun only gave as much light and heat at mid-day as a coal fire a mile away; we should all be frozen solid, while the earth’s atmosphere would surround us in the form of an ocean of liquid air. So far as we know, there is no possibility of the sun suddenly beginning to behave like S Doradus, but we shall see later that the possibility of its behaving like Wolf 359 is not altogether a visionary dream.
Surface -Temperature And Radiation. Sirius has been found to have the highest surface-temperature of all the stars near the sun; it is about 11,000 degrees, or nearly double that of the sun. Going further afield, we find many stars with far higher surface-temperatures. For instance, Plaskett’s star is credited with a temperature of 28,000 degrees, although it must be admitted that a substantial element of uncertainty enters into all estimates of very high stellar temperatures.
At the other extreme, stellar temperatures ranging down to about 2500 degrees are comparatively common. The lowest temperatures of all are confined to variable [ p. 271 ] stars of a very special type (long period variables) in which the light-variation is accompanied by, and indeed mainly arises from, a variation in the temperature of the star’s surface. The temperature of these stars when at the lowest, ranges down to 1650 degrees, which is but little above the temperature of an ordinary coal fire. In many of them, the temperature varies through a large range, but it never sinks so low that the star becomes completely invisible. Thus there is a range of temperature below about 2500 degrees which no star is known to occupy, except for the long-period variables which only enter it at intervals. This would seem to suggest that the number of absolutely dark stars in the sky is relatively small. Other lines of evidence lead to the same conclusion. If a star ceased to shine, its gravitational pull would still betray its existence. Although we could not detect a single dark star in this way, we could detect a multitude. If a great proportion of stars were dark, we should probably suspect the existence of the dark stars from their effects on the motions of the remainder, so that general gravitational considerations preclude the possibility of there being a great number of dark stars.
So far as our present knowledge goes, the temperature of stellar surfaces ranges, in the main, from about 30,000 degrees down to about 2500, the lower limit being extended to about 1650 for long-period variables at their lowest temperatures.
Apart from the long-period variables, this is only a 12 to 1 range, so that the temperatures of the stars are more uniform than either their luminosities or their weights. We must, however, remember that a star’s radiation per square inch is far more fundamental than its surface-temperature, and that a 12 to 1 range [ p. 272 ] in the latter involves a range of over 20,000 to 1 in the former. If we include the long-period variables, there is a range of about 110,000 to 1 in the emission of radiation per square inch.
In terms of horse-power, the sun emits energy at the rate of 50 horse-power per square inch, a star with a surface-temperature of 1650 degrees emits only 0.35 horse-power per square inch, while Plaskett’s star, with a surface-temperature of 28,000 degrees, emits about 28,000 horse-power per square inch. In plain English, each square inch of this last star pours out enough energy to keep an Atlantic liner going at full speed, hour after hour, and century after century. And the energy emitted per square inch by the surfaces of various stars covers the whole range from the power of a liner to that of a man in a row-boat.
Size. The four stars of largest known diameter are the following:
| Star | Diameter in terms of sun | Diameter in miles |
|---|---|---|
| Antares | 450 | 390,000,000 |
| α Herculis | about 400 | 340,000,000 |
| ο Ceti (at max.) | 300 | 260,000,000 |
| Betelgeux (average) | 250 | 210,000,000 |
All these diameters have been measured directly by the interferometer. On the scale used in figs. 17 to 20, in which the sun is about the size of a sixpence, the circle necessary to represent ο Ceti would be as large as the floor of a good-sized room, while the second star of the system (for ο Ceti is binary) would be the size of a grain of sand. We may obtain some idea of the immense size of these stars by noticing that every one of their diameters is larger than the diameter of [ p. 273 ] the earth’s orbit, so that if the sun were to expand to the size of any one of them we should find ourselves inside it.
These stars must be exceedingly tenuous. Antares, for instance, occupies 90,000,000 times as much space as the sun, so that if its substance were as closely packed, it would weigh 90,000,000 times as much as the sun. Yet, in actual fact, it probably has only about 40 or 50 times the sun’s weight, the difference between this number and 90,000,000 arising from the difference between the densities of Antares and the sun. On the average a ton of matter in the sun occupies considerably less than a cubic yard; in Antares it occupies rather more space than the interior of Saint Paul’s Cathedral. Yet a detailed study of stellar interiors shews that we can attach but little meaning to an average of this sort. It is quite likely that matter at the centre of Antares is packed nearly (but not quite) as closely as matter at the centre of the sun (p. 291 below). The huge size of Antares is probably due mainly to an enormously extended atmosphere of very tenuous gas, and there is not much point in striking an average between this and the compact matter at the centre of the star.
The mysterious objects known as planetary nebulae, of which examples are shewn in Plate II (p. 28), ought perhaps to be regarded as stars of still larger diameter. At the centre of each of these the telescope discloses a comparatively faint star with an extremely high surface-temperature. Surrounding this is the nebulosity from which these objects derive their somewhat unfortunate name. This is in all probability merely an atmosphere of even greater extent than that surrounding the four stars of our table. Van Maanen [ p. 274 ] estimates the diameter of the nebulosity of the Ring Nebula in Lyra (fig. 2 of Plate II) to be 570 times that of the earth’s orbit, or about 106,000,000,000 miles. This nebulosity, however, differs from the atmosphere of an ordinary star in being very nearly transparent; we can see through 106,000,000,000 miles of the Ring Nebula but can only see a few tens or hundreds of miles into an ordinary star.
At the other extreme of size, the smallest known star, van Maanen’s star (p. 268) is just about as large as the earth ; over a million such stars could be packed inside the sun and still leave room to spare. And yet its weight is in all probability comparable, not with that of the earth, but with that of the sun ; at a guess it may have about a fifth of the sun’s weight. To pack a fifth of the sun’s substance inside a globe of the size of the earth, the average ton of matter must be packed into a space of about the size of a small cherry — ten tons or so to the cubic inch. The solidity of the earth suggests that its atoms must be packed pretty closely together, but the atoms in van Maanen’s star must be packed 66,000 times more closely.
How is it done? As we shall shortly see, there is only one possible answer. The atom consists mostly of emptiness — we compared the carbon atom to six wasps buzzing about in Waterloo Station. Let us break the atom up into its constituent parts, pack these together as closely as they will go, and we see the way in which matter is packed in van Maanen’s star. Six wasps which can roam throughout the whole of Waterloo Station can nevertheless be packed inside a very small box.
Giants and dwarfs. There is a continuous series of stars between the limits of weight we have [ p. 275 ] mentioned, and the same is true of the limits of temperature (and so also of colour) and of size.
Within these specified limits, I can find you a star of any weight or of any colour or of any size you like. But this does not mean that you may specify the weight and colour and size of the star you want, and that I will undertake to find it for you; if the weight is right the colour may be wrong, and so on. For instance, if you ask for a red star I can find you a very heavy one or a very light one, but it is no good your asking for one of intermediate weight. So far as we know, red stars of intermediate weight simply do not exist. The same is true as regards size — there are no red stars of intermediate size. Hertzsprung noticed [ p. 276 ] in 1905 that the red stars could be divided sharply into two distinct classes characterised by large and small size — he called them Giants and Dwarfs. Russell, studying the question further in 1913, confirmed Hertz- sprung’s earlier conclusions, and shewed that the giant-dwarf division extended to stars of other colours than red.
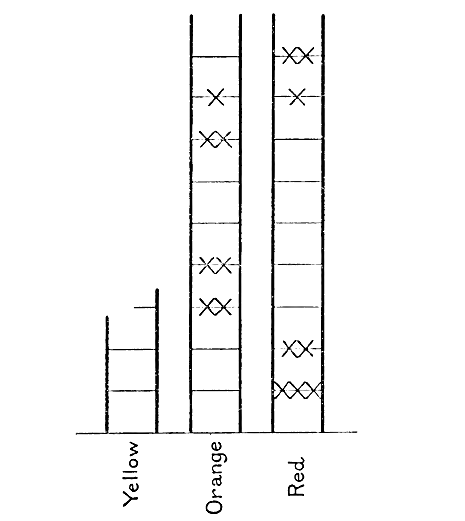
Imagine that we have a series of coloured ladders, one for each colour of star — red, orange, etc. Take all the red stars and stand them (in imagination) on the different rungs of the red ladder. Do not merely place them on at random; arrange them in order of their luminosities, placing those of highest luminosity uppermost. Further let several stars stand on the same rung if their luminosities are about equal. To make the arrangement definite, let each rung of the ladder represent 5 times higher luminosity than the rung immediately below it, so that each rung has a definite luminosity associated with it[3].
With this agreement we are now ready to proceed. We take our red stars and place each on the appropriate rung of the red ladder, and so on for each other colour. The result is shewn diagrammatically in fig. 21, the different stars being represented by crosses.
The red stars will be found to lie as on the right of the diagram, Hertzsprung’s division into giants and dwarfs being very clearly marked. The orange stars lie as on the next ladder to the left ; as Russell found, the division again appears, but is less marked.
The Russell diagram. Let us make ladder diagrams of this kind for each colour of star, and put [ p. 277 ] them side by side in their proper order, so as to represent stars of all possible colours. We obtain a diagram of the kind shewn in fig. 22. This type of diagram was introduced by Russell in 1913, and is now generally known as a Russell diagram.
The letters at the top of the diagram represent spectral types of stars, because these provide a better and more exact working classification than the names of colours. The colours which approximately correspond to the various spectral types are indicated at the bottom of the diagram.
Only a very few sample stars are shewn, but all known stars are found to be concentrated around the positions of these few typical stars. Broadly speaking, there are two distinct and disconnected regions which are occupied by stars. First, and most important, is a region shaped rather like a reversed y : the central line of this region is marked in by a continuous thick line, following a determination of its position by Redman. Second, there is a smaller region near the left-hand bottom corner of the diagram. The stars Avhich occupy this region are very faint, and have far higher surface- temperatures than other stars of similar luminosity.
We have already seen how a star’s diameter can be calculated from its surface-temperature and luminosity. This amounts to the same thing as saying that two stars which occupy the same position in the Russell diagram must have the same diameter. Thus there is a definite diameter associated with each point in the diagram, and we can map out stellar diameters in the diagram, just as we can map out heights above sea- level on a geographical map, by a system of “contour lines.” In the present case the “contour lines” prove to be a system of almost parallel curves. These lie [ p. 278 ] roughly as shewn by the broken lines in fig. 22, all stars lying on any one line having the same diameter.
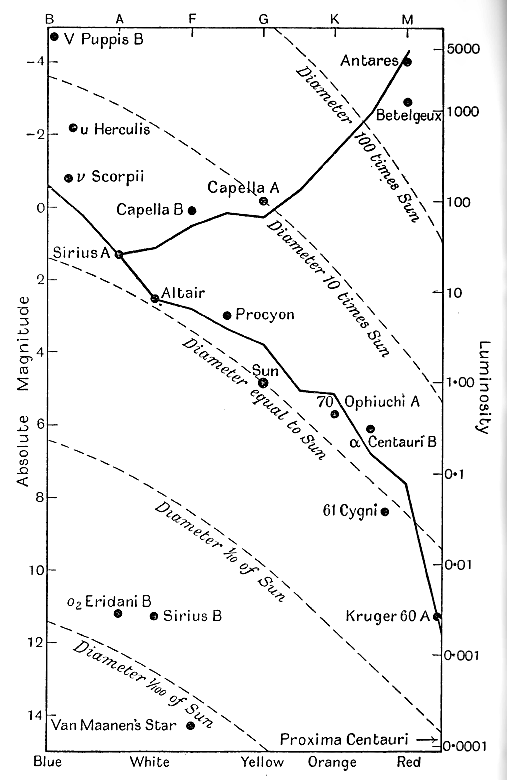
This diagram throws a flood of light on the general question of stellar diameters. We see at once that stars of the biggest diameters — 100 times the sun’s diameter or more — must necessarily be red stars of high luminosity. And in actual fact the stars of large diameter shewn in the table on p. 272 are all red and have very high luminosities; they are red giants.
The majority of the stars in the sky lie in the belt which runs across the diagram of fig. 22 from top lefthand to bottom right-hand. This is known as the “main-sequence.” The position of this band with reference to the “contour lines” of diameters shews that main-sequence stars are of moderate diameters. The brightest of all may have twenty times the diameter of the sun, while the faintest may have only about a twentieth of the sun’s diameter, but they all have diameters which are at least comparable with that of the sun. The sample of stars from near the sun, which we have already discussed, provides many instances of main-sequence stars; we have, in order of decreasing luminosity :
| Star | Luminosity | Diameter (in terms of sun) |
|---|---|---|
| Sirius A | 26.3 | 1.58 |
| Procyon A | 5.5 | 1.80 |
| α Centauri A | 1.12 | 1,07 |
| Sun | 1.00 | 1.00 |
| α Centauri B | 0.32 | 1.22 |
| τ Ceti | 0.32 | 0.95 |
| ε Indi | 0.15 | 0.82 |
| Kruger 60 A | 0.0026 | 0.33 |
| Kruger 60 B | 0.0007 | 0.17 |
| Wolf 359 | 0.00002 | 0.03 |
[ p. 280 ] This table shews clearly how stellar luminosity and diameter decrease together as we pass down the main- sequence.
The remaining group of stars in fig. 22, those in the bottom left-hand corner, are generally known as “white dwarfs.” Their position in the diagram shews that their diameters must be excessively small. The vicinity of the sun provides three examples of this class of star, as shewn in the following table :
| Star | Luminosity | Diameter (in terms of sun) |
|---|---|---|
| Sirius B | 0.0026 | 0.03 |
| ο2 Eridani B | 0.0031 | 0.018 |
| van Maanen’s star | 0.00016 | 0.009 |
In addition to these, the faint companion of ο Ceti is certainly a white dwarf, while Procyon B may be. These are the only known examples of white dwarfs, but the extreme faintness of these stars makes them very difficult of detection, so that it is quite likely that they are fairly frequent objects in space.
In the table on p. 279, the main-sequence stars were intended to be arranged in the order of luminosity, but this happens also to be the order of weights. The weights of three of the stars are unknown; those of the remainder are as follows :
| Star | Luminosity | Weight (in terms of sun) |
|---|---|---|
| Sirius A | 26.3 | 2.45 |
| Procyon A | 5.5 | 1.24 |
| α Centauri A | 1.12 | 1.14 |
| Sun | 1.00 | 1.00 |
| α Centauri B | 0.32 | 0.97 |
| Kruger 60 A | 0.0026 | 0.25 |
| Kruger 60 B | 0.0007 | 0.20 |
[ p. 281 ] Like the luminosities, the weights fall off steadily as we pass down the main-sequence, although, as already remarked, weight falls far less rapidly than luminosity.
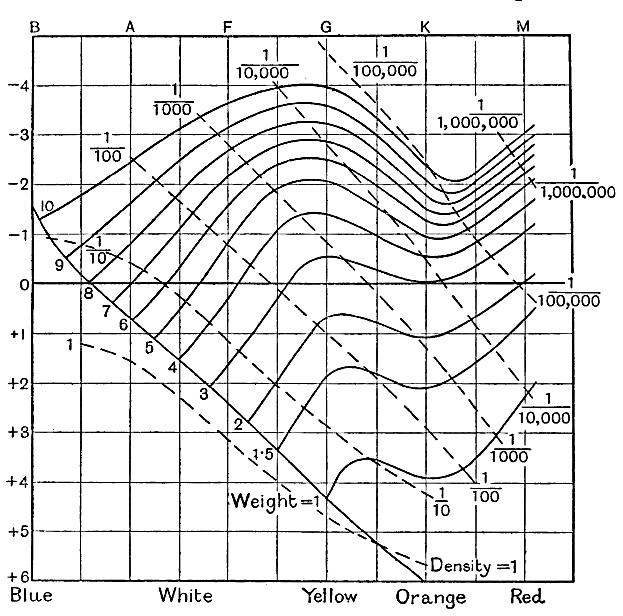
The only stars whose weights can be measured directly are the components of binary systems, and these are relatively few in number. Seares found, however, that the weights of binary systems conformed to the law of equipartition of energy already explained in Chapter III, so that it is highly probable that other stars which are not binary also conform, for it is difficult to imagine any reason why binary systems should attain to a state of equipartition sooner than other stars. It will be remembered that this state is defined by a purely statistical law connecting the weights and speeds of motion of stars, so that the fact that a system of stars has attained this state can give no information as to the weight of an individual star whose speed is known, but it makes it possible to determine the average weight of any group of stars in terms of their average speeds of motion. In this way Seares has determined the average weights of stars of different assigned luminosities and spectral types — in other words, the average weights of the stars represented at the various points in the diagram of fig. 22. The results he obtained are shewn by the thick curved lines in fig. 23. The arrangement of these curves confirms the inference we have drawn from a few selected stars; the weight of main-sequence stars falls off steadily as we pass down the sequence from high luminosity to low.
These curved lines specify the average weight of the stars represented at each point in the Russell diagram, and the diameters are already known from fig. 22. From these two data the mean density of the [ p. 282 ] star can of course be calculated. The mean densities as calculated by Seares are shewn by the broken lines in fig. 23.
This completes our collection of observational material. We now turn to the far more difficult problem of discussing what it all means. Here we leave the firm ground of ascertained fact, to enter the shadowy morasses of conjecture, hypothesis and speculation. The questions we shall discuss are some of the most interesting in the whole of astronomy, to which it must [ p. 283 ] be admitted that science has so far obtained only lamentably dusty answers. The reader who is hot for certainties may prefer to read something other than the remainder of the present chapter.
¶ The Physical Condition Of The Stars
The foregoing collection of observational data has provided abundant proof that stars to certain specifications do not exist at all. To put the same thing in another way, there are certain regions in the Russell diagram which are wholly unoccupied by stars.
To take the most conspicuous instance of all, there are no stars at all to the left of the main-sequence in the Russell diagram (fig. 22), until we come to the quite detached group of white dwarfs. Why are there no stars in intermediate conditions? Why, to make the example still more precise, does no star exist of the same colour as Sirius but with only a tenth of its luminosity? Why do we have to go down to the white dwarf o ο2 Eridani B, with a luminosity of only a ten-thousandth of that of Sirius, before we can find a star to match Sirius in colour?
A hypothesis which occurs naturally to the mind is that the main-sequence stars and the white dwarfs may form distinct groups because they are of entirely different ages — they may represent distinct creations. As stars age they decrease in weight and in luminosity, so that it is natural to interpret the small weights and extremely low luminosity of the white dwarfs as evidence of an age far greater than the age of the normal main-sequence stars. Yet this hypothesis does not appear to be tenable.
With the single exception of van Maanen’s star, every star which is either known or suspected to be [ p. 284 ] a white dwarf forms one component of a binary system, and in every case its companion is a main-sequence star or (in the case of ο Ceti) a red giant. We have already seen how rare it is for two stars to approach near to one another in space. It must be an almost inconceivably rare event for two stars, originally moving as independent bodies, so to meet in their random wanderings, that the big one “captures” the little one, and they henceforth journey together through space. For it can be shewn that, for such an event to occur, something more than a close approach is needed; a close approach must take place in the presence of yet a third star, so that no fewer than three stars must chance to come near one another simultaneously in their wanderings through the vast emptinesses of space. It is almost inconceivable that this should happen in a single instance, but it is straining the probabilities too far to suppose that it has happened in the case of every single known white dwarf but one. Thus we have to suppose that the white dwarfs and their more normal companions have been together since birth, and so were born at the same time out of the same nebula.
The difference between white dwarfs and main- sequence stars cannot, then, be a mere difference of age, and it would seem as though there must be some physical reason militating against the existence of stars in intermediate conditions. Taking a more general view of the question, we are led to investigate whether the absence of stars built to certain specifications can be attributed to such stars needing physical properties which nature cannot provide. This leads directly into the general question of the structure and mechanism of the stars. [ p. 285 ]
¶ The Internal Constitution Of The Stars
Most investigations on the structure of the stars have proceeded on the supposition that their interiors are gaseous throughout. Without accepting this supposition as final truth, we may adopt it for the moment, for the purely opportunist reason that it provides the most convenient line of approach to an excessively difficult problem.
A mathematical theorem, generally known as Poincare’s theorem, proves to be of the utmost service in discussing the internal state of a gaseous star. We have seen how Helmholtz thought that the energy of the sun’s radiation might come from the sun’s contraction, each layer falling in upon the next inner layer as the latter shrunk, and transforming the energy set free by its fall into heat and light. It is easy to estimate how much energy would be set free by a contraction of this kind. For instance, Lord Kelvin calculated that the contraction of the sun, as it shrunk from infinite size to its present diameter of 865,000 miles, would liberate about as much energy as the sun now radiates in 50 million years. In terms of ergs, the sun’s shrinkage would liberate 6 x 1048 ergs of energy.
Poincare’s theorem states that the total energy of motion of all the molecules in any gaseous star whatever is equal to precisely half the total energy which the star would have liberated in shrinking down to its present size. The theorem is true quite independently of whether the star ever has so shrunk or not : nothing is involved but the present state of the star.
One interesting consequence is that the further a gaseous star shrinks, the hotter it becomes; if a star [ p. 286 ] shrinks to half its present size, the total energy set free by its shrinkage from infinite size is doubled, so that the total energy of motion of its molecules is doubled, and therefore its average temperature is doubled. This is a special case of what is generally known as Lane’s law.
Let us go on with our calculation for the special case of the sun. Poincare’s theorem tells us that, if the sun is gaseous, the total energy of motion of all its molecules is 3 x 1048 ergs. The next thing we want to know is how many molecules there are in the sun. The sun’s weight is 2 x 1033 grammes, but how many molecules are there to a gramme? The answer of course depends on the type of molecule concerned; there are 3 x 1023 molecules in a gramme of hydrogen, 2 x 1022 in a gramme of air and only 2.5 x 1021 in a gramme of uranium.
If we suppose the sun to be made of air, it must consist of 4 x 1055 molecules, so that the average energy of motion of each molecule must be 7.5 x 10-8 ergs, and this represents an average temperature, for the sun’s interior, of 375 million degrees. In 1907 Emden, by a different calculation, found that if the sun were made of air, the temperature at its centre would be 455 million degrees. Apart from details, it is clear that the interior temperature of a sun made of air would be one of hundreds of millions of degrees.
So far all study of stellar interiors had proceeded on the supposition that the stars were formed of complete atoms or even molecules. In 1917, I made a simple calculation, of the type already explained on p. 141, and found that the quanta of radiation which fly about at such temperatures would be energetic enough not merely to break up the molecules of air into atoms, but [ p. 287 ] also to strip all, or nearly all, of the electrons from the atoms. At such temperatures each molecule of air would break up into its constituent nuclei and electrons just as surely as, on a hot day, a lump of ice breaks up into its constituent molecules. The electric forces which, in quieter surroundings, would unite the electrons and nuclei, first into atoms and then into complete molecules, find themselves powerless against the incessant hail of rapidly moving projectiles and the shattering blows of quanta of high energy ; it would be like trying to build a house of cards in a hurricane. A sun consisting of molecules of air proves to be an inconsistency, a contradiction; our hypothesis has defeated itself, and we must start again from the beginning.
We may start wherever we like, but the conclusion which we must finally reach is that, no matter what kind of molecules the sun consists of, the heat at the sun’s centre will break them up, either completely or nearly so, into their constituent nuclei and electrons. The same is true for all other stars, and this introduces an extreme simplification into the problem of the interior constitution of the stars. We cannot say how many complete molecules there are to a gramme without knowing the nature of the molecules, but once let these molecules be broken up into their constituent parts, and we know at once the total number of constituent parts, nuclei and electrons, which go to make up a gramme. For, the atomic weights of all elements except hydrogen are nearly double their atomic numbers (p. 110). Hence, as Eddington first pointed out, the total number of nuclei and protons in a fully broken-up atom of any substance except hydrogen must be equal to about half the atomic weight [ p. 288 ] of the atom. We may probably disregard the possibility of a star consisting to any great extent of hydrogen. If so, the number of constituent parts in a gramme of fully broken-up stellar matter must be about 3 x 1023, regardless of the type of molecule from which these parts originate. And when we know the total number of such parts in any star, it becomes easy to calculate the temperature of the star’s interior, either from the theorem of Poincare just mentioned or otherwise. The temperature will be the same as though the star were made of unbroken molecules of hydrogen.
Emden calculated in 1907 that the central temperature of a sun of this kind would be about 31,500,000 degrees. Later and more refined calculations by Eddington led to an almost identical temperature, but some still later calculations of my own give the substantially higher figure of 55,000,000 degrees. There is no need for the moment to discuss which of these figures is nearest the truth. Their diversity will indicate what kind of degree of uncertainty attaches to all calculations of this type.
It is easy to see the physical necessity for this high temperature. The heat which flows away from the sun’s surface must first have been brought there from its interior. Heat only flows from a hotter to a cooler place, and a vigorous flow of heat is evidence of a steep temperature gradient. The temperature must rise sharply as we pass from the sun’s surface towards its centre, and this rise, continued along the whole 433,000 miles to the centre, must result in a very high temperature indeed being reached there.
The calculated central temperature of 30 to 60 million degrees so far transcends our experience that [ p. 289 ] it is difficult to realise what it means. Let us, in imagination, keep a cubic millimetre of ordinary matter — a piece the size of an ordinary pin-head — at a temperature of 50,000,000 degrees, the approximate temperature at the centre of the sun. Incredible though it may seem, merely to maintain this pin-head of matter at such a temperature — i.e. to replenish the energy it loses by radiation from its six faces — will need all the energy generated by an engine of three thousand million million horse-power; the pin-head of matter would emit enough heat to kill anyone who ventured within a thousand miles of it.
High though this temperature is, calculations shew that it would not suffice to break up the stellar molecules completely. It would strip the atoms of all their electrons down to the K-rings (p. 134), but these would remain intact. It needs temperatures even higher than those we are now considering to strip the K-ring electrons from the nucleus of an atom. This result is true for the whole range, from about 30 to 60 million degrees, within which the temperature of the sun’s centre is at all likely to lie, and it is true almost independently of the atomic weight or atomic number of the atoms of which we suppose the sun to be built.
Thus if the sun is wholly gaseous, its central parts must consist of a collection of atoms stripped down to their K-rings, but not beyond, flying about independently like the molecules of a gas, and with them, also flying about like the molecules of a gas, all the stripped-off electrons which originally formed the L-ring, the M-ring, etc., of the atoms, the whole being at a temperature of somewhere between 30 and 60 million degrees. As we pass outwards towards the sun’s surface we come to lower temperatures, at which the atoms [ p. 290 ] are less completely broken up. Finally, close to the sun’s surface, we may meet atoms which are completely formed except perhaps for one or two of their outermost electrons. In the surfaces of the coolest stars of all, we even find complete molecules, as, for example, the molecules of titanium oxide and magnesium hydride, which shew themselves in the spectra of the red stars.
When the internal constitution of other stars is investigated in the same way, all main-sequence stars are found to have about the same central temperatures as the sun. Moreover, this is not the only property which they have in common. Fig. 23, which exhibits Seares’ calculations of mean stellar densities, shews that the mean densities of main-sequence stars are all approximately the same, except for comparatively small deviations at the two extremities.
The mean density of the sun is 1.4, which means that the average cubic metre in the sun contains 1.4 ton of matter. At the sun’s centre, the density is about 100 times this, so that a cubic metre there contains about 140 tons of matter. For comparison, a cubic metre of lead contains only about 11 tons. If all stars were built on the same model as the sun, any two stars which had the same mean density would also have equal densities at their centres. But in stars having several times the weight of the sun, a new factor comes into play, namely pressure of radiation — the pressure which radiation exerts in virtue of the weight it carries about with it. In most stars this pressure is insignificant in comparison with the pressure produced by the impact of material atoms and electrons, but in very massive stars it is large enough to influence the structure of the star. It is to this that [ p. 291 ] the very massive stars whose diameters are tabulated on p. 272 owe their abnormally large size. It is a general consequence of the disturbing effects of radiation-pressure, that the weight of a very massive star is far more concentrated in its central regions than that of a lighter star, so that if a light and a massive star have the same average density, the latter will have by far the higher density at its centre. When this disturbing factor is allowed for, all stars in the upper part of the main-sequence are found to have approximately the same densities in their central regions, a density about equal to that at the centre of the sun, which we may estimate at 140 tons to the cubic metre. And we have already seen that the central regions of these stars have also approximately the same temperatures as the centre of the sun, whence it follows that their physical conditions are all substantially the same. Thus the atoms in the central regions of all these stars must be broken down to the same extent as the atoms in the central regions of the sun. The K-rings of electrons survive intact, but the outer rings are transformed into a hail of electrons flying about like independent molecules.
With sufficient accuracy for our present purpose, all the stars on the main-sequence, except perhaps those at its extreme lower end, may be supposed to be in the same physical condition. On account of this property, the main-sequence forms an admirable baseline from which to carry out a survey of the Russell diagram in respect of the physical conditions of stellar interiors.
Fig. 22 shews that a star to the right of the mainsequence has a greater diameter than a main-sequence star of the same weight. Consequently the energy [ p. 292 ] it would emit in shrinking to its present diameter is less, and hence its molecular energy of motion is less (by Poincare’s theorem). It follows that its internal temperatures are lower, and its atoms are less completely broken up. Red giants such as Antares are found only to have central temperatures of from one to five million degrees, and their atoms probably retain intact not only their K-rings of electrons, but also their L-rings and part at least of their M-rings.
To the left of the main-sequence we come to a region in which stars, if they occurred at all, would have shrunk further, and so would have higher temperatures and more thoroughly broken atoms. Actually no stars are encountered until we come to the white dwarfs. Calculation shews that the central temperatures of these must be many hundreds of millions of degrees at least, and that their atoms must be stripped of electrons right down to the nuclei. Except for a small number of atoms which may have escaped this general fate, the stellar matter must consist of nuclei stripped absolutely bare, and of free electrons, all flying independently through the star. The high densities of these stars provide a convincing proof of the accuracy of this result. The mean density of Sirius B is certainly over 50,000, while that of van Maanen’s star is probably over 300,000. There is no way in which matter can be packed as closely as this, except that of stripping the atoms of electrons right down to their bare nuclei.
The clearest general impression we can form of the Russell diagram in terms of physical condition is probably obtained as follows:
We think first of two detached bands of stars, one, the white dwarf group, formed by stars in which all [ p. 293 ] the electrons are torn off the atoms; and the other, the main-sequence, formed of stars in which the atoms are still surrounded by their K-rings of electrons, while the exterior rings have been torn off. Starting from about the middle of the main-sequence is the spur branch leading up to the red giants, as shewn in fig. 22. As we pass along this, the internal temperatures of the stars decrease, so that the stellar atoms are less broken up than in main-sequence stars. In the red giants at the extreme end, even M-ring electrons may still remain.
¶ Russell’s Hypothesis
Two entirely different explanations of this distribution of stars have been suggested. In 1925 Russell put forward a theory which centred primarily around the fact that the temperatures at the centres of the main-sequence stars are all very nearly equal. Let us simplify the situation for a moment by imagining it to be an ascertained fact that the temperatures at the centres of all stars are precisely the same, say 32,000,000 degrees. If this were a sure fact, it would be natural to conjecture that the stars had some sort of controlling mechanism by which they continually adjusted their central temperatures to this exact figure, so that if ever the temperature fell below 32,000,000 degrees the mechanism would come into play and raise the temperature to precisely this amount, while if it increased to above this figure, the mechanism would come into play and depress it. Such controlling mechanisms are of course common in engineering practice ; there are for instance the safety-valves which keep the pressure in a boiler always uniform, the [ p. 294 ] Watts-governor which keeps an engine going always at the same rate of speed, and the thermostat which keeps the temperature of a room constant.
A mechanism is already known for raising the temperature at a star’s centre. If a star is not generating any energy at all in its interior, either by the annihilation of matter or otherwise, its emission of radiation causes it to shrink, and this, as we have seen (p. 285), causes its temperature to rise. Thus it is easy to keep a star’s central temperature up to 32,000,000 degrees by arranging that no energy shall be generated so long as the temperature at the centre is below 32,000,000 degrees, and this is the main hypothesis on which Russell’s theory is based. He supposes that no energy at all is generated by matter at temperatures below 32,000,000 degrees, but that, as soon as this temperature is reached, matter begins to annihilate itself in sufficient quantity to provide for the radiation of a star.
The trouble with the theory is that it seems impossible to regulate the temperature from the other end. A star whose central temperature is below 32,000,000 degrees must be contracting without generating heat. The contraction will not stop dead the moment the critical temperature is attained; its momentum will carry it on until the central temperature substantially exceeds 32,000,000 degrees. As soon as the temperature seriously exceeds 32,000,000 degrees at the centre, that of a substantial piece of the star will be 32,000,000 degrees or higher. The annihilation of all this matter must produce a profusion of heat which would raise the temperature of the star still further, resulting in more and more annihilation of matter, until finally the whole star disappeared [ p. 295 ] in a flash of radiation. Indeed Russell’s theory supposes that matter at 32,000,000 degrees is in a similar condition to gunpowder at its flash point. Mathematical analysis then shews that a star whose centre is at a temperature of 32,000,000 degrees would be in the state of a keg of gunpowder with a spark at its centre, and — well, “ohne hast, ohne rast” hardly describes the subsequent course of events.
Eddington has suggested that the stability of the stars might be saved by imagining a time-lag between the instant at which matter attained the critical temperature necessary for annihilation and the instant at which this annihilation occurred. It has not yet been proved that the proposed remedy could be made effective, but even if it could, other difficulties remain. As the normal star inhabits the main-sequence, Russell supposed it to be a property of normal matter to annihilate itself at a temperature of about 32,000,000 degrees, the supposedly uniform central temperature of all main-sequence stars. It then became necessary to introduce further special assumptions to explain the luminosity of white dwarfs and of stars on the red giant spur line, whose centres are at temperatures very different from 32,000,000 degrees. He accordingly supposed that such stars contained other types of matter which dissolved into radiation at temperatures which were respectively higher and lower than 32,000,000 degrees. Even if the stability difficulty could be overcome, this latter series of assumptions seems to me to be so artificial as to compel the abandonment of this interesting theory.
A discussion of the difficulties of Russell’s theory led me to undertake a mathematical investigation of the stability of stars in general, and this was found to [ p. 296 ] provide a simple and somewhat unexpected explanation of the otherwise incomprehensible distribution of stars in the Russell diagram; it is in brief that the unoccupied regions of the diagram represent stars in an unstable condition. I do not know what proportion of astronomers accept this explanation; some, whose opinion I value, do not. I do not think that much so far written in this book would be seriously challenged by competent critics, but it is only fair to say that at this point we are entering controversial ground.
¶ The Hypothesis Of Liquid Stars
Let us begin by imagining an enormous number of stars built on all possible plans, out of all kinds of substances. Mathematical investigation shews that some of these stars may be unable to shine with a steady light for either or both of two reasons — they may explode, like a heated keg of gunpowder, or they may have an inherent tendency to contract or expand without limit. Whether a star escapes the first pitfall or not depends mainly upon the properties of the substance of which it is built; whether it escapes the second depends mainly upon the way it is built. The two pitfalls are not altogether distinct, and when we consider the stability of wholly gaseous stars of enormously great weight, we find that the pits on the two sides of the path merge into one, or at most only a narrow strip of safe ground is left between them. Nevertheless stars of enormously great weight are known to exist, and continue shining steadily. If then, these stars are wholly gaseous, they must occupy the one safe spot of ground between the two pits, and this informs us both as to the way they are built and as [ p. 297 ] to the properties of the substance of which they are built.
We find that such stars only escape both pitfalls if their substance possesses properties which appear very improbable, and contrary to anything of which we have any experience or knowledge in physics; in brief, for such a star to remain stable, the annihilation of its matter must proceed at a rate which depends on the temperature. Such a property seems in every way contrary to the physical principles explained in Chapter II, as it is to all our expectations of atomic behaviour. The annihilation of matter is a far more violent change, and involves quanta of far higher energy, than mere radio-active disintegration, and as the latter process is not affected by temperature changes, it hardly seems possible that the process of annihilation should be, at any rate until we reach temperatures of the order of the 2,200,000,000,000 degrees tabulated on p. 144 [4].
We have, however, already found indications that the stars are not purely gaseous, since purely gaseous masses could not form close binary systems of the type observed in the spectroscopic binaries (p. 222). Such systems can only be formed out of a mass which simulates the properties of a liquid rather than those of a gas; the mass need not be wholly liquid, but there must be a considerable divergence from the state of a pure gas, at any rate in its central regions. Additional evidence to the same effect will also emerge later (pp. 310, 311).
As soon as we admit that the interiors of the stars need not be in a completely gaseous state, the whole situation changes, even a slight departure from the [ p. 298 ] gaseous state being found to impart a great deal of additional stability to the star. If a star of great weight is purely gaseous in its structure, the region of stability between the two pitfalls is reduced to a narrow strip, and only by treading this can the star escape the alternative fates of exploding or collapsing. But if the star has a liquid, or partially liquid, centre, this strip of safe land is so wide that, consistently with stability, the stellar material may have exactly the property that we should a priori expect to find, namely, that its annihilation proceeds, like radio-active disintegration, at the same rate at all temperatures. If the substance of the star has this property, the star can be in no danger of exploding, for a mass of uranium or radium does not explode whatever we do to it. And mathematical analysis shews that if the centre of the star is either liquid, or partially so, there is no danger of collapse; the liquid centre provides so firm a basis for the star as to render a collapse impossible.
These considerations suggest the two complementary hypotheses:
-
That the annihilation of stellar matter proceeds spontaneously, not being affected by the temperature of the star.
-
That the central regions of the stars are not in a purely gaseous state; their atoms, nuclei and electrons are so closely packed that they cannot move freely past one another, as in a gas, but rather jostle one another about like the molecules of a liquid.
If we have been right (p. 149) in attributing the observed highly penetrating radiation in the earth’s atmosphere to the annihilation of matter in distant astronomical bodies, then the first hypothesis is confirmed. For the radiation could not retain its observed [ p. 299 ] high penetrating power if it had already penetrated any great thickness of matter. The struggle of passing through matter lengthens the wave-length of all kinds of radiation (the quanta get weaker all the time), and so diminishes its penetrating power. Thus, wherever the highly penetrating radiation originated, it must have got out into empty space without much of a struggle, and this is the same thing as saying that it must have originated in matter at a comparatively low temperature. Thus the existence of the highly penetrating radiation proves that matter can be annihilated in great quantities at quite low temperatures ; the high temperatures of stellar interiors are not needed, as Russell’s theory asserts, for annihilation to occur.
A simple calculation shews that there can be no appreciable annihilation of the earth’s substance. In the sun about one atom in every 1019 is annihilated every minute; if even a ten-thousandth part as many atoms as this were annihilated in the earth, its surface would be too hot for human habitation. We can no longer explain this by saying that the sun is hot and the earth cool, so that annihilation goes on in the former but not in the latter. We must rather suppose that the atoms in the sun are of a different type from those on earth. Solar atoms spontaneously annihilate themselves, terrestrial atoms do not, or at least do not to any appreciable extent.
The second of our hypotheses, that the central regions of the stars are more like a liquid than a gas, is, as we have seen, a necessary consequence of the first, but independent evidence in its favour is found in the formation of binary systems by fission. For in Chapter iv (p. 222) we saw that a star could only break up by fission if it had a liquid, or a nearly liquid, centre.
[ p. 300 ]
¶ The Stability Of Stellar Structures
For the present, let us tentatively accept the hypothesis that the generation of stellar energy occurs spontaneously, like the disintegration of radio-active atoms. The atoms which are responsible for the light and heat of the stars may be regarded as super-radioactive atoms which spontaneously annihilate themselves and so change their substance into radiation.
We have already seen that, on this view of the mechanism of generation of stellar energy, a star can only continue to shine steadily if its central regions are not in a purely gaseous condition. A star built on foundations of highly compressible gas meets the same fate as a house built on sand: it collapses. A purely gaseous star is a dynamically unstable structure, and must continually contract until the atoms in its central regions are so closely packed that their state can no longer be regarded as gaseous. Then, and then only, can the star exist permanently as a stable structure. Thus the central regions of any actual permanent star, the sun for instance, must be in a state which for brevity we may describe as liquid.
Now let us imagine the sun to be expanded to ten times its present diameter. This would diminish its density to a thousandth part of its original value. The actual sun is 40 per cent, more dense than water, but the expanded sun would only be as dense as ordinary atmospheric air. The atoms and electrons, having moved ten times farther apart, would be so distant from one another that the new sun might be regarded as wholly gaseous. Thus it would be dynamically unstable and could not remain in its wholly gaseous state.
[ p. 301 ] Our imaginary expanded sun is of course no longer a main-sequence star in the Russell diagram. In expanding the sun to ten times its present size we move it off the main-sequence into a region entirely vacant of stars — in fact, into the great gulf which lies between the red giants and the red dwarfs (see fig. 22, p. 278). Thus, it appears that even if we deliberately place a star in this region, it does not stay there but immediately contracts until it gets on to the main- sequence. May not this explain why the region in question is untenanted by stars?
Next let us imagine the sun contracted to a tenth of its present diameter, so that its atoms and electrons move ten times nearer to one another. Its mean density is thereby increased from 1.4 to 1400 times that of water, and its central density from about 140 to 140,000. You may check me here by pointing out that if the sun is already in a liquid state it cannot be compressed to any such extent — a liquid cannot usually have its density increased a thousand-fold. But we have already noticed that halving a star’s diameter doubles its temperature throughout. In the same way reducing a star’s diameter to a tenth increases its temperature ten-fold, so that the sun’s central temperature will be increased from, say, 50 million degrees to 500 million degrees. And at this latter temperature atoms hardly exist any longer as such — the stellar matter consists almost entirely of free electrons and nuclei. And these are so minute, that the increase of the sun’s mean density from 1.4 to 1400 times the density of water is not only possible, but leaves the sun’s substance in a state which may best be described as gaseous. Once again, then, the new sun is dynamically unstable. It would be [ p. 302 ] represented by a point well to the left of the main- sequence, near the middle of the unoccupied region between the main-sequence and the white dwarfs, but as it is unstable it cannot maintain its position here. Again we see that even if we place a star in this region it cannot stay there. And, again — may it not be that the reason why this region is unoccupied is that it represents unstable stars?
Once more you may check me. If I have made my point, it has been by the help of the rise of temperature which accompanies contraction. When we imagined the sun to expand, ought we not to have considered the fall of temperature which accompanies expansion? The answer is that we ought, but it would have made no difference. Lowering the temperature will cause a number of L-rings, and possibly also of M-rings, of electrons to re-form, so that the new atoms will be of larger size, but they will not lose their freedom of motion sufficiently to make the sun stable. It would have been different if we had been discussing a star of 10 or 50 times the sun’s weight; then it can be shewn that the re-formation of K- and L-rings would have produced a series of stable configurations. And the spur branch in the Russell diagram exists to provide a home for just such stars.
The whole problem is too complicated to be discussed satisfactorily in this fragmentary way; its proper discussion involves very complicated mathematical analysis. Mathematical discussion shews that the Russell diagram can be divided into regions representing stable and unstable configurations in the manner shewn in fig. 24.
The unstable areas are so marked; the remaining areas are stable. The dots which form a sort of back [ p. 303 ] ground to the diagram represent 2100 stars whose absolute magnitudes are known through their parallaxes having been determined spectroscopically at Mount Wilson. The observational material is not perfect, for considerable uncertainty attaches to all spectroscopic parallaxes of B-type stars, and A-type stars are almost unrepresented because it is practically impossible to obtain their parallaxes by the [ p. 303 ] spectroscopic method. The theoretical curves are probably still more imperfect, yet, such as they are, they seem to suggest very forcibly that the occupied and unoccupied regions coincide with those representing stable and unstable configurations ; after making all possible allowances for the imperfections both of theory and of observation, too much agreement remains to be explained away as mere coincidence.
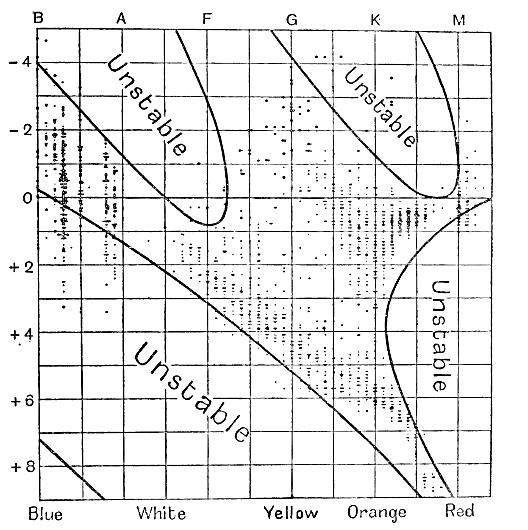
Thus the conclusion to which mathematical discussion seems to lead is that the regions in the Russell diagram which are occupied, represent stars whose central regions are in a liquid, or nearly liquid, state. All other stars are unstable, so that the corresponding regions in the Russell diagram are necessarily vacant. To put it in less technical language, all the stars in the sky must have liquid, or nearly liquid, centres.
Here we have a piece of the puzzle which seems to fit on to the piece we unearthed in Chapter IV, where we found that a star could only break up by fission if it had a liquid, or nearly liquid centre. Evidence accumulates that the stars have liquid rather than gaseous centres.
Criticism of the foregoing hypothesis — generally described as the “liquid-star” hypothesis — has mainly taken the form that the diameters of the K-rings of atoms are so small that the K-ring atoms in the sun’s central regions cannot possibly be packed closely enough to involve any substantial departure from the gaseous state. It is difficult to discuss, and still more to meet, this criticism without knowing the precise diameters of these K-ring atoms. We of course know the diameters assigned to the K-ring by Bohr’s theory (p. 129), but no one any longer contends that this theory gives a true picture of the atom. It provides [ p. 305 ] a good working model within limits, but we do not know where the limits end. The only practical experience we have of K-ring atoms is with helium atoms; Bohr’s theory assigns to these a diameter of 0.54 x 10-8 cms. Yet solid and liquid helium provide a practical illustration of the closeness with which helium atoms can be packed; in these each atom occupies a sphere of diameter 4 x 10-8 cms., or over 400 times the space allotted to it by Bohr’s theory. It looks as though we are still far from definite knowledge of the dimensions of K-rings of electrons.
The new wave-mechanics of Schrodinger draws a very different picture of atomic interiors from the simpler theory of Bohr which it is rapidly superseding. Even the electron is something very different from the electron of Bohr’s old theory. It is the oldfashioned electron only when it is at an infinite distance from the nucleus. As it gradually approaches this nucleus, it undergoes a metamorphosis of a kind which no one has yet succeeded in describing, and it is utterly impossible to say what form it may have assumed by the time it is doing what we call “describing a K-ring orbit.” All we know about the K-ring orbit is its energy, and it seems impossible to predict the amount of space occupied by such an orbit until we have a better knowledge of the qualities of the article which is describing it.
We have of course to admit that the physical evidence, such as it is, seems to point to K-ring atoms being substantially smaller than is needed for the liquid-star hypothesis. But the astronomical evidence seems to me stronger and more reliable, and to point in exactly the opposite direction. And here we must leave the puzzle until further pieces come to light.
[ p. 306 ] Until we know the kind of atoms of which a particular star is composed, we cannot calculate the extent to which they will be broken up by the temperature of the star’s interior. As a consequence, the theoretical curves of demarcation between stable and unstable configurations cannot be calculated without assuming definite atomic numbers for the stellar atoms.
The curves shewn in fig. 24 have been drawn for an atomic number of about 95, this being slightly higher than the atomic number, 92, of uranium. This atomic number was selected because it was found to produce the best agreement between theory and observation, but we shall see that other considerations justify our choice.
¶ Stellar Structure
A star, like a house or a pile of sand, is a structure which would collapse under its own weight were it not that each layer is held up against gravity by the pressure which the next inner layer of the star exerts upon it. This pressure is not, like ordinary gaspressure, the result of the impacts of complete molecules. It is produced in part by the impact of a certain number of atoms which have been stripped of electrons almost or quite down to their nuclei, but to a far greater extent by the impact of a hail of free electrons. In massive stars, an additional pressure is produced by the impact of radiation which, as we have seen, carries weight about with it, and so exerts pressure on any obstacle it encounters. The combined impacts of free electrons, of atoms (or bare nuclei), and of radiation prevent the star from falling in under its own gravitational attraction.
[ p. 307 ] This gives a reasonably good snapshot picture of a star’s structure. The corresponding picture of its mechanism is obtained by thinking of the nuclei as α-ray particles, of the free electrons as β-ray particles, and of the radiation as γ-rays (although in most stars the main bulk of the radiation has the wave-length of X-rays). All these thread their way through the star, and, precisely as in laboratory work, the β-rays are more penetrating than the α-rays, and the γ-rays are more penetrating than either.
The Transport Of Energy In A Star. We have seen how the heat of a gas is merely the energy of its molecular motion. Conduction of heat in a gas is usually studied by regarding each molecule as a carrier of energy; when it collides with a second molecule the energy of the two colliding molecules is redistributed between them, and in this way heat is transported from hotter to cooler regions. Each molecule has a power of transport which is jointly proportional to its energy of motion, its speed of motion, and its “free-path” — the distance it travels between successive collisions.
In the interior of a star, there are three distinct types of carrier in action — atoms (or bare nuclei), free electrons, and radiation. We can compare their relative capacities as carriers by multiplying up the energy, speeds and free-paths of each. For this purpose the “free-path” of radiation may be taken to be the distance the radiation travels before 37 per cent, of it has been absorbed, since it can be shewn that this is the average distance it carries its energy. On carrying out the calculation, the carrying capacity of both nuclei and electrons is found to be insignificant in comparison with that of the radiation. The nuclei [ p. 308 ] and electrons may have the greater amount of energy to carry, but owing to their feebler penetrating powers, the distance over which they carry it, their free-path, is far less than that of the radiation. Their speed of transport is also less, since radiation transports its energy with the velocity of light. In this way it comes about that practically the whole transport of energy from the interior of a star to its surface is by the vehicle of radiation.
This general principle was first clearly stated by Sampson in 1894. He also shewed how the temperature of any small fragment of a star’s interior must be determined by the condition that it receives just as much radiation as it emits, but his detailed applications were vitiated through his using an erroneous law of radiation. Twelve years later, Schwarzschild independently advanced the same idea, and expressed it in mathematical equations of “radiative equilibrium” which have formed the basis of every subsequent discussion of the problem.
Just because radiation completely outstrips atoms and electrons in carrying energy from a star’s interior to its surface, it follows that the build of a star must be determined by the opacity of the matter in its interior. If this is altered, the carrying power of the radiation is altered, and this affects the whole structure of the star. A star whose interior was entirely transparent could not retain any heat at all; its whole interior would be at a very low temperature and the star would be of enormous extent. On the other hand, in a very opaque star, all energy would remain accumulated at the spot at which it was generated, so that the interior temperature would become very high and the star’s diameter would be [ p. 309 ] correspondingly small. It is, of course, the intermediate cases which are of practical interest, but the extreme instances just mentioned shew how a star’s build depends on its opacity.
Unfortunately it is impossible to obtain any sort of direct measurement of the opacity of stellar matter. We cannot even measure the opacity of terrestrial matter under stellar conditions, since the interiors of the stars are at incomparably higher temperatures than any available in the laboratory. However, we know that the opacity of stellar matter is due to the atoms, nuclei and free electrons of which it is composed checking the onward journey of radiation, and although we cannot obtain a sample of stellar matter, we know fairly definitely how many atoms, nuclei and electrons such a sample would contain. Thus it becomes a matter of theoretical calculation to determine its opacity.
Such a calculation was carried through by Dr Kramers of Copenhagen in 1923, and his results gained general acceptance. Quite recently Mr Gaunt of Cambridge has made a much more refined calculation, and obtained results which agree very closely with those originally given by Kramers. In so far as these results can be tested in the laboratory, they agree well with observation. And, although there is a big gap between laboratory conditions and stellar conditions, it is difficult to see how Kramers’ formula could fail in the stars.
From this formula we can determine the build of the stars completely, or, if the build of the star is supposed to be known, Kramers’ formula tells us the rate at which energy flows to its surface (this depending entirely on the opacity of the star’s substance), and this in turn tells us at what rate energy must be generated inside the star for it to be able to remain [ p. 310 ] in equilibrium in the configuration in question. As might be expected, configurations of different diameters are found to require different rates of generation of energy. In nature, a star must adjust its diameter to suit the rate at which it is generating energy; in so doing it fixes not only its diameter but also its surface-temperature, colour and spectral type. If a star’s rate of generation of energy were suddenly to change, the star would expand or contract until it had assumed the radius and temperature suited to its new rate of generation of energy.
Detailed calculation shews that, for wholly gaseous stars, large diameters correspond to feeble generation of energy and vice versa. Thus, if the stars were wholly gaseous, red giants would be less luminous than main- sequence stars of the same weight. Seares’ diagram, reproduced on p. 282, shews that the reverse is actually the case, a red giant emitting from 10 to 20 times as much total radiation as an equally massive main-sequence star. This provides evidence against the stars being wholly gaseous, but there is stronger evidence than this. For wholly gaseous stars, the thick lines shewn in Seares’ diagram would be straight slant lines, slanting upwards to the left. The wide divergence between such a system of slant lines and the curves shewn in fig. 23 gives some indication of the extent to which the condition of stellar matter diverges from the purely gaseous state.
According to Kramers’ theory, the opacity of matter depends on the atomic numbers and atomic weights of the atoms of which it is built, a large clot of matter in the form of a massive atomic nucleus being far more effective in absorbing radiation than a large number of small clots of the same total [ p. 311 ] weight. Everyday terrestrial experience shews that this is so. It is for this reason that the physicist and surgeon both select lead as the material with which to screen their X-ray apparatus; they find that a ton of lead is far more effective in stopping unwanted X-rays than a ton of wood or of iron. If we knew the strength of an X-ray apparatus, and the total weight of shielding material round it, we could form a very fair estimate of the atomic weight of the shielding material by measuring the amount of X-radiation which escaped through it.
A very similar method may be used to determine the atomic weights of the atoms of which the stars are composed. A star is in effect nothing but a huge X-ray apparatus. We know the weights of many of the stars, and the rate at which they are generating X-rays is merely the rate at which they are radiating energy away into space. If we could cut each atomic nucleus in a star into two halves, we should halve the opacity of the star, so that radiation would travel twice as far through the star before being absorbed. If the star were wholly gaseous, this would result in its expanding to four times its original diameter, and in its surface-temperature being halved. It follows that we can calculate the atomic weight of the atoms of which a star is composed from the weight, luminosity and surface-temperature of the star.
The atomic weights of a number of stars, which I calculated on the supposition that the stars were wholly gaseous, came out in practically every case higher than that of uranium, which is the weightiest atom known on earth. They not only proved to be higher, but enormously higher; so high indeed, as to seem utterly improbable. Again the explanation seems to [ p. 312 ] be that the stars are not wholly gaseous. As soon as stellar interiors are supposed to be partially liquid, the calculated atomic weights are reduced enormously. They can no longer be determined exactly, but the atomic number of about 95 to which we were led from a consideration of the Russell diagram seems to be entirely consistent with all the known facts.
Indeed other considerations seem to suggest that the atomic numbers of stellar atoms must be higher than 92. A priori stellar radiation might either originate in types of matter known to us on earth or else in other and unknown types. When once it is accepted that high temperature and density can do nothing to accelerate the generation of radiation by ordinary matter, it becomes clear that stellar radiation cannot originate in types of matter known to us on earth. Other types of matter must exist, and as, with two exceptions, all atomic numbers up to 92 (uranium) are already occupied by terrestrial elements, it seems probable that these other types must be elements of higher atomic weight than uranium.
These super-heavy atoms must not be expected to disclose their presence in stellar spectra, for these only inform us as to the constitution of the atmospheres of the stars. And as the lighter atoms float to the top it is these, in the main, which figure in stellar spectra. If the sun’s atmosphere had contained any considerable number of super-heavy atoms when the planets were born, some of them ought still to exist in the earth. There cannot be any great number, or their high generation of energy would betray them. The simplest view seems to be that the heavier atoms sink to the centre in the stars, and that the earth was formed mainly or solely out of the lighter atoms which had floated to the sun’s surface.
¶ Stellar Evolution
We have supposed that the stars were born initially as condensations in the outer fringes of spiral nebulae. These condensations would, from the mode of their formation, necessarily be of all sorts of sizes, and subject only to the single restriction that none of them could be below a certain limit of weight. Thus we should not expect the stars, either at birth or subsequently, to be all of the same size or weight, or all in the same physical condition. The stars would start their existences at different points in the Russell diagram, but we may imagine that their initial positions are limited to those parts of the diagram which can be occupied by stars — either, as the liquid-star hypothesis would suggest, because these are the only stable configurations, or else for some other reason so far undiscovered. Each year a star loses a certain amount of weight, and its rate of generating energy, and so also its luminosity, are correspondingly reduced, with the result that it moves to a new position in the diagram. Turning to Seares’ diagram of stellar weights on p. 282, we may think of the curves of equal weight as a flight of steps — very uneven steps, it is true — each representing a lower weight than the one above. Whatever a star’s evolution may be, it is essential that it should always be down the steps : any upward step is impossible.
We can trace out two possible paths of stellar evolution in the Russell diagram which involve no entry into regions unoccupied by stars — two roads along which the stellar army may march as they transform their substance into radiation. The first is of course the “main-sequence,” which a great number of considerations suggest to be the main line of march of the stellar army. The branch which starts from the [ p. 314 ] red giants in the Russell diagram represents a second possible line of march, a certain number of stars travelling along this branch until they reach the main-sequence as blue or white stars, and then travelling down the lower half of the main-sequence to end as faint red stars passing on to ultimate extinction.
Progress along each of these roads is accompanied by a continuous shrinkage in the size of the star, its diameter steadily decreasing. This is not the same thing as saying that the star’s density continually increases, for the star is continually diminishing in weight, so that even if the star’s density remained the same, its diameter would decrease. Nevertheless a study of Seares’ determinations of mean densities, as shewn in the diagram on p. 282, suggests that there is a continuous increase of density, although this becomes very slight in the middle reaches of the main-sequence.
Practically every theory of stellar evolution which has ever been propounded has imagined the inarch of the stellar army to be of the same general type as that just described, although perhaps present-day opinion is inclined to treat the main-sequence as the principal line of march, whereas earlier theories supposed the j’oungest stars to march solely along the red-giant branch, only joining the main-sequence with middle age. The first serious theory of all, that of Lockyer, was expressed in terms of branches of ascending and descending temperature, these together forming the last-mentioned line of march in the Russell diagram. A theory which Russell propounded in 1913 again assigned to the stars the lines of march just described. It also attempted a physical explanation, since abandoned, as to why the stars followed these [ p. 315 ] particular paths rather than others. His more recent theory of 1925 only differed from his earlier theory in giving the new explanation, which we have already discussed (p. 293), as to why the stars followed these particular paths.
At present, it is probably fair to say that nearly, and perhaps quite, all astronomers are agreed that the evolutionary paths of the stars are of the general type we have described. Some stars start as red giants, some as blue, some possibly in intermediate conditions. As they age, all move downwards in the Russell diagram, their various paths converging to a point at the fork of the reversed γ shewn in fig. 22, and after passing this point they move down the main-sequence. On the other hand, there is the widest difference of opinion as to the physical interpretation which is to be assigned to these paths. Most astronomers are probably suspending judgment until some definite observational evidence is obtained to decide between conflicting theories.
When the stars first came into being as flecks of fiery spray thrown off by spinning nebulae, they would consist of mixtures of atoms of all kinds, some perhaps being so short-lived as to transform themselves almost at once into radiation, and others having such long lives that they may properly be described as permanent. Except for a small number of radioactive atoms, the earth must consist entirely of atoms of this latter type. Calculation shews that terrestrial atoms must have enormously longer lives than the average stellar atom, otherwise their self-annihilation would make the earth too hot for habitation. The permanent atoms in a star contribute almost nothing to its energy-generating capacity, and so merely add to its [ p. 316 ] weight. The shortest lived atoms of all contribute greatly to the star’s generation of energy while adding but little to its weight. In general the shorter the life of any type of atom, the greater the proportion of its numbers annihilated per year, and so the greater the amount of energy it generates per ton of weight.
A star begins life with a large proportion of short- lived atoms, and so at first generates energy furiously. As it ages, the shortest lived atoms disappear first, and in so doing reduce the average energy-generation of the star per ton so that, as a star’s weight decreases, so also must its rate of generation of energy per ton. Finally all the atoms with much energy-generating capacity have disappeared, and the star is left, a shrunken and diminished mass of atoms which have very little capacity for generating radiation.
To put the same thing in another way, the rate at which a star generates energy per ton is proportional to the death-rate in its population of atoms. To say that Sirius generates 16 times as much energy per ton as the sun is only another way of saying that the average atom in Sirius has only a sixteenth of the expectation of life of the solar atoms; their death-rate is 16 times as high. As those types of atoms which have the highest death-rate gradually die off in any star, the average death-rate of the population decreases, or, in other words, as a star ages its capacity for energy- generation per ton decreases.
This agrees with the findings of observational astronomy. The most massive stars not only generate more energy than less massive stars, as is in any case to be expected; they also generate enormously more energy per ton. This is illustrated by the following list of main-sequence stars :
[ p. 317 ]
| Star | Weight (in terms of sun) | Generation of energy (ergs per gramme) |
|---|---|---|
| Pearce’s Star A | 36.3 | 15,000 |
| V Puppis A | 19.2 | 1,000 |
| Sirius A | 2.45 | 29 |
| Sun | 100 | 1.90 |
| ε Eridani | (0.45) | 0.26 |
| Kruger 60 B | 0.20 | 0.021 |
Seares’ diagram of stellar weights ([#p282]) shews that this is a general property of the stars. To repeat our former metaphor, the stars squander their substance lavishly in their youth, while they have plenty left to spend, but parsimony comes over them with old age. Theoretical considerations have now given us an explanation of this phenomenon.
The same diagram shews that two stars of the same weight do not usually have the same luminosity. In general, giant stars on the spur branch leading out to the red giants have substantially higher luminosities than the main-sequence stars of equal weight. We have already noticed how a red giant may emit as much as 1 0 or 20 times the radiation of an equally massive main- sequence star. The same story is repeated when we pass from the main-sequence stars to the white dwarfs. Main-sequence stars emit enormously more radiation — anything up to 500 times more — than white dwarfs of equal weight. This is illustrated by the three following white dwarfs, which may be compared with the last three stars of the preceding table:
| Star | Weight (in terms of sun) | Generation of energy (ergs per gramme) |
|---|---|---|
| Sirius B | 0.85 | 0.0027 |
| ο2 Eridani B | 0.44 | 0.002 |
| van Maanen’s star | (0.20) | (0.00055) |
[ p. 318 ] We have hitherto supposed generation of energy to be spontaneous and so unaffected by changes of physical conditions. Yet the facts just mentioned seem to suggest that this can hardly be the whole truth of the matter. To state the objection in terms of a concrete instance, Sirius A and its white dwarf companion Sirius B must in all probability have been born at the same time out of the same nebula (p. 284), yet the former generates 4000 times as much energy per ton as the latter. It seems improbable that so great a difference can be attributed to different types of atoms; the common origin of the two stars almost precludes this. We know that the atoms are in different physical conditions in the two stars; in Sirius A they have retained their K-rings intact, while in Sirius B, the white dwarf, they are completely broken up into bare nuclei and free electrons. If the two components of Sirius consist of essentially the same types of atoms, as their common origin would lead us to expect, then the enormous difference in the rates at which these atoms generate energy would seem to depend on the different physical conditions of their atoms.
The considerations brought forward in Chapter III make it highly probable that a star’s rate of generation of energy depends on the physical condition of its atoms. We there supposed stellar energy to be generated through electrons coalescing with protons; protons exist only in atomic nuclei, and purely physical considerations led to the conjecture that the only electrons which can coalesce with a particular proton are those which are momentarily describing orbits around the nucleus in which the proton resides. A study of stellar structure supports this hypothesis, for if energy could be generated by free electrons falling [ p. 319 ] into nuclei, it can be shewn that the whole star would be unstable and would explode in a flash of radiation. On this hypothesis, a star in which only a few atoms have any electrons left in orbital motion can of course generate but little energy. This at once explains the feeble energy-generating powers of the white dwarfs, and also gives an inkling as to why the red giants, in which L- and M-rings of electrons survive, generate more energy than main-sequence stars of equal weights.
As a star ages and its weight decreases, it continually has to pick out new configurations such as make its emission of energy equal to its internal rate of generation of energy. The same star may be a red giant, a main-sequence star and a white dwarf in turn. Stripped of technicalities this means that a star continually adjusts its diameter to suit its varying rate of generation of energy.
On the hypothesis just considered, a star alters both its emission and its generation of energy on changing its diameter. At every instant it has to select a diameter for which the two exactly balance. The star has so large a range of rates of generation, according as it has few or many electrons left in orbital motion, that it is likely always to be able to find a configuration of equilibrium. At any rate all the stars in the sky appear to have done so, with the exception of the long period variables which are continually expanding and contracting as though they could not hit upon a diameter at which their income and expenditure of energy would just balance.
This same hypothesis immediately makes it possible for all the great variety of stars in the galactic system to be of approximately the same age, and so to have [ p. 320 ] been all born out of the same nebula. The most luminous galactic stars can hardly have been generating energy at their present rate for more than about 100,000 million years — any longer age would require an impossibly high weight to start with. Yet the motions of the stars indicate that even these highly luminous stars must have been in existence for at least 50 times this period. The apparent contradiction disappears if we admit that the extreme luminosity of the very brightest stars may be a recent development, and that for perhaps 98 per cent, of its life such a star was losing but little energy because most of its atoms were stripped bare of electrons and so were immune from annihilation. The requisite proportion of 98 per cent, may seem suspiciously large, but we have stated an extreme case; we need only demand so large a proportion in the case of a very rare type of star: probably not more than one star in ten million is of such a type.
In their earlier dormant state, these stars, which are now so luminous, would in effect have been white dwarfs of enormous weight. Observational astronomy provides no evidence that any such stars exist, but there is certainly no evidence that they do not exist. Very massive stars are known to be very rare objects, so that in all probability we should have to travel a long distance from the sun before finding one, and then it might be so distant as to be invisible from the earth. In any case, a very distant star of feeble luminosity would be exceedingly likely to escape detection. We could not infer that no such stars existed from the fact of none having yet been found.
Moreover, it is far from absolutely certain that such stars have not been found. Very massive white dwarfs [ p. 321 ] ought to have higher surface-temperatures than either massive main-sequence stars or than the known white dwarfs, all of which are of small weight. A whole group of stars is known — the O-type stars — whose spectra indicate very high temperatures indeed. These are usually interpreted as stars of enormous luminosity at enormous distances, but it is possible that some at least of them may be stars of feeble luminosity at moderate distances. In particular the central stars of the planetary nebulae are of types O and B. But whereas the normal main-sequence star of these spectral types is generally about a thousand times as luminous as the sun, the central stars of the planetary nebulae are found to be considerably less luminous than the sun. Dr Gerasimovic has recently shewn that 52 of these stars have an average luminosity only about two-thirds of that of the sun. Other observers have found even lower luminosities. As the surface-temperatures of these stars must be of the order of 30,000 degrees, they must be minute in size; indeed a simple calculation shews that they can hardly have more than about a tenth of the sun’s radius.
Not only are they small in size, but there are indications that they are of great weight. Spectroscopic evidence shews that in many cases the surrounding nebulae are in rotation, and, just as with the galaxy (p. 69) and the huge extra-galactic nebulae (p. 71), their weights can be calculated from their observed speeds of rotation. These seem to indicate average weights of something like 40 or 50 times the weight of the sun. Campbell and Moore, of Lick Observatory, have calculated that the planetary nebula N.G.C. 7009 must have 162 times the weight of the sun, but many factors combine to make this estimate rather uncertain.
[ p. 322 ] All this goes to suggest that the central stars of the planetary nebulae must, in all probability, be regarded as “white dwarfs” of enormous weight. It seems possible that they are exactly the type of star needed by our theory. The 52 planetary nebulae already mentioned have the same average distance from the sun, and the same distribution with respect to the galaxy, as the O-type stars, so that it is possible that O-type stars and planetary nebulae are forms assumed either successively or alternatively in the course of evolution of similar bodies. It should be mentioned that the planetary nebulae exhibit spectral displacements which, if interpreted in the ordinary way, would indicate that they are moving with very high speeds, in some cases reaching hundreds of miles a second. Such speeds would be entirely inappropriate to stars of large weight. Yet this objection rather defeats itself, for if the spectral shifts really arose from high speeds of motion, the highest of the observed speeds would suffice to carry the planetary nebulae possessing them clear of the galactic system altogether; they would be random travellers through our system of stars, whereas their orderly arrangement and concentration near the galactic plane suggests very forcibly that they are permanent members of it. Thus the observed large shifts of the spectral lines can hardly indicate large speeds in space; some other interpretation must be found. Professor Perrine considers that they arise in the main from internal motions, contraction, expansion and rotation of the nebulae. If so, the motions in space cannot be determined, but at least they no longer present any difficulty. If these stars are, as our hypothesis requires, white dwarfs of very great weight and small radius, their spectra ought [ p. 323 ] to exhibit a relativity displacement to the red of the same type as that actually observed in Sirius B. It is possible that this may be found to present a more serious difficulty, although it is also possible that it again may prove to be merged in the large observed displacements.
In view of all this, it seems quite possible that both the planetary nebulae, and also other O- or B-type stars of feeble luminosity, may be very massive stars in the dormant condition contemplated by the hypothesis we have just been discussing. In brief, we imagine that a massive star may have its weight conserved through existing as a planetary nebula or a dwarf O-type star for millions of millions of years, and then burst out as a highly luminous star with all the appearance of extreme youth. But there is at present insufficient observational evidence either for or against such a hypothesis. Some pieces of the puzzle are missing, and we can only wait until they turn up.
White dwarfs. Apart from these hypothetical massive white dwarfs, astronomers generally regard ordinary white dwarfs as the final stage in stellar evolution. There is general agreement that they are stars with central temperatures so high that their atoms are stripped bare of electrons, but there is no general consensus of opinion as to why stars shrink to this condition.
On the liquid star hypothesis, the unoccupied regions in the Russell diagram represent unstable configurations. Usually a slight loss of weight by a star merely moves it to a new position in the diagram contiguous to the old one. Sometimes, however, this slight move may happen to carry the star into an unstable region of the diagram, in which case it will [ p. 324 ] hurriedly traverse this region, until finally it ends up in some entirely different stable configuration.
The liquid star hypothesis explains the white dwarf state quite simply as the final state to which a star shrinks cataclysmically when its generation of energy is no longer sufficient to entitle it to a place in the main-sequence. In this state the star radiates so little energy that annihilation and decay are almost entirely checked. We have seen that if the sun went on radiating at its present rate for 15 million million years, its whole weight would be transformed into radiation. By contrast, van Maanen’s star can, and probably will, go on radiating at its present rate for 15 million million years without losing more than about a thousandth part of its present weight. We may think of the white dwarf state as a final state from which change and decay have so nearly disappeared that a star which shrinks to this state acquires a new lease of life for a period of thousands of millions of millions of years — we can only wonder to what purpose.
¶ Footnotes
This is shewn in fig. 15, the area of the 3000 degree curve being only a sixteenth of the area of the 6000 degree curve. ↩︎
The large round images of stars shewn in the frontispiece result merely from over-exposure, and have nothing to do with the sizes of the stars. ↩︎
For purely practical reasons the height is not taken proportional to the luminosity but to its logarithm; without some such device as this it would be impossible to represent the range of more than 1,000,000 to 1 in the observed luminosities of red stars. ↩︎
This provides a further objection to Russell’s hypothesis, which, to avoid confusion, was not mentioned on p. 295. ↩︎