© 2009 Carmelo Martínez
© 2009 Urantia Association of Spain
¶ Introduction
Contemplating the starry sky, I have often wondered where Jerusem and the mansion worlds would be, worlds in which we may live our next lives, and where Salvington, where we will one day meet our creator Michael of Nebadon who lived two millennia ago in this planet.
I have also wondered which of those stars that I was seeing were in Satania or in our local universe.
I have not found the answer to these questions in The Urantia Book, but I have found precise information about the size of the administrative units of creation closest to us.
This work reflects my current thoughts on the matter and the calculations I have made from the information I have found in The Urantia Book.
The page and paragraph numbers of the citations used are included between parentheses and within the text of this work, and the texts of these citations are copied in the final annex in the same order in which they appear in this work.
¶ The spheres of space
The Urantia Book classifies the spheres of space as follows:
- The suns - the stars of space.
- The dark islands of space.
- Minor bodies in space comets, meteors and planetesimals.
- The planets, which include the inhabited worlds.
- Architectural spheres—worlds made to order. For this work I want to focus only on the first two types.
On the one hand, the suns are the hot spheres that shed light and energy (UB 41:3.1). They are the stars that we see in the starry skies and are observed with telescopes.
On the other hand, the dark islands are spheres that do not emit light or energy. Its origin is diverse (UB 15:5.10-11): some are the result of increases in energy in transmutation of space. Others are accumulations of matter that circulates through space. These spheres have never been hot.
Finally, others are already extinguished suns.
It should be noted that the islands are not normally visible like the suns are (we do not see them in starry skies or be observed with telescopes), and therefore they must be detected by the gravitational effects they produce on other visible spheres.
¶ Physical composition of Satania
Satania has more than seven thousand planetary systems (UB 41:2.2), but only has about two thousand suns (UB 41:3.1). This means that the center of some five thousand systems is a dark island. Presumably the planets in these systems with dark islands are not habitable.
There are therefore about two thousand planetary systems with planets that have the possibility of harboring life. However, Satania will eventually be made up of a thousand inhabited planets, which means that there will be more than a thousand systems (there are systems with more than one inhabited planet) that will not have inhabited planets.
¶ Volume of Satania and Nebadon
The Urantia Book gives a clear indication of the density of suns in space. It does not indicate whether this density is the same throughout the superuniverse, or even in all superuniverses, but it seems clear that it is applicable to the entire local universe (the title of the paper is Physical Aspects of the Local Universe, and it seems likely that it may apply to the rest of the universe). of the disk of the Milky Way.
The paragraph in question is UB 41:3.2 and ensures that the space to house the suns is equivalent to what a dozen oranges would have inside our planet if it were hollow.
From this clear indication the volumes of Satania and Nebadon will be roughly deduced.
For this, we will start from the information in the aforementioned paragraph. The volume of twelve suns, if they had the size of oranges, would be that of our planet, which is , where RT is the radius of the Earth, which is approximately 6,370 kilometers. The volume is therefore 1,082,696,932,000 cubic kms. The volume occupied by 12 medium-sized suns (1,600,000 km in diameter according to the aforementioned paragraph) will be the ratio between the volume of a sun and that of an orange. If we consider that an orange is 8 cm in diameter (0.00008 km), the ratio of the cubes of both values turns out to be 1.6000.0003 / 0.000083 = 8 E30. Applying this relation to the volume of the Earth, it results for the volume occupied by twelve suns, a figure of 8.661575 E42 cubic kilometers or, what is the same, 10,228.53 cubic light years. If we assume that Satania will not have more suns (although it will have more inhabited planets) the volume occupied by two thousand suns, and therefore the volume of Satania, would be 10,228.53 / 12 * 2000 = 1,704,755 cubic light years .
The volume of Nebadon, which has or will have 10,000 systems, would be 1.704755 E10 cubic light years.
¶ Mean distance between suns
To estimate the mean distance between the suns, it is necessary to assume a certain distribution of the suns. Currently the suns are distributed in an apparently random way, but to estimate the average distance it is necessary to assume that they are distributed according to a regular lattice containing the same number of suns for the given volume. The model is equivalent to the distribution of atoms in a crystal lattice.
If we suppose associated to each sun a virtual sphere whose center is the sun and whose diameter is the average distance between the suns sought, the studies carried out in this regard indicate that the problem is equivalent to the packing of equal spheres.
These studies indicate that maximum packing occurs with either the hexagonal close-packed or the cubic face-centered close-packed distribution. The theoretical packing factor that results from these distributions is approximately 0.74 and is shown to be the maximum possible.
If we return to the case of the twelve suns that occupy a volume of 10,228.53 cubic light years, and we apply to this volume the packing factor (10,228.53 * 0.74 = 7,569.11) we will obtain the volume of the twelve virtual spheres that surround the twelve suns. The volume of the virtual sphere of a single sun will therefore be 7,569.11 / 12 = 630.76 cubic light years, and the diameter of said sphere will be 10.64 light years, which is the mean distance among the suns that we are looking for.
The close-packed hexagonal or close-cubic distribution may be more than just a gimmick for calculating the distance between the suns. We know that each administrative unit of the universes advances towards finite perfection, the attainment of which supposes the entry of that unit into the ages of light and life. This achievement implies both a spiritual perfection of all the personalities of that unit from the finite point of view, as well as a material perfection of all the component spheres and their interconnections and interrelationships (suns, planets, circuits, distributions, etc.). We might suppose that in this state of finite perfection the suns have been brought into one of the above distributions, which distribute them according to a regular lattice.
¶ Shapes and sizes of Satania and Nebadon
Calculating the volumes of Satania and Nebadon, estimating their sizes depends on the shape they take in space.
If we assume that they take a cubic shape, the sides will be approximately 120 and 2,575 light years respectively.
If we assume that they are spherical, their diameters will be approximately 148 and 3,195 light years respectively.
But both ways have advantages and disadvantages. With cubes it is possible to occupy 100% of the available space, with spheres a maximum of 74%. Spheres minimize the mean distance to the center of all points in the volume in question, cubes do not. There are various polyhedra that are capable of covering 100% of the space by stacking (among them the cube), but it coincides that the domain of a sphere in the compact cubic packing (one of those with maximum occupancy) is the rhombic dodecahedron , and the rhombic dodecahedron is one of the polyhedra with which 100% of the space can be occupied. This polyhedron has a more “spherical” shape than the cube and therefore a smaller mean distance from the center than the cube.
To reach a compromise between the total occupation of space and the minimization of distance, we can therefore imagine that the administrative units of creation adopt the form of the rhombic dodecahedron, within which the suns (to come to light and life) are located. distributed according to a grid that corresponds to that of a centered cubic compaction. In this case, and based on the formula for the volume of a rhombic dodecahedron (), it is calculated that the edges of Satania and Nebadon would be approximately 82 and 1,769 light years respectively.
It is also interesting to know the diameter of the sphere circumscribed to a rhombic dodecahedron a, which for Satania and Nebadon would be approximately 189 and 4,085 light years respectively.
¶ Distances to Jerusem and Salvington
Assuming that Jerusem is the center of a sphere, a rhombic dodecahedron, and a cube, we get maximum distances of 74, 95, and 85 light-years respectively, and estimated mean distances of 56, 57, and 59 light-years, respectively.
As for Nebadon, the maximum distances would be 1,600, 2,040 and 1,820, and the averages of 1,200, 1,220 and 1,270 light years respectively. It is found that the average distance of a dodecahedron is somewhat greater than that of the sphere (the smallest possible) but clearly less than that of the cube. The dodecahedron therefore seems to be a better polyhedron from the point of view of the economy of transport and communications than the cube, both being capable of covering 100% of the available space. However, the maximum distances are greater in the dodecahedron, indicating that the extent of the farthest areas is greater in the cube than in the dodecahedron.
According to UB 39:3.9, the transport seraphim that carry beings to and from the constellation headquarters reach speeds nearly three times the speed of light. Presumably the rest of the transport seraphim travel at those speeds as well. Therefore, the times to reach the enseraphim from the furthest point of the system to the capital, Jerusem, will be approximately 25, 32 and 28 years respectively for the three possible forms analyzed; and mean times of about 19, 19, and 20 light years respectively.
Likewise, the times to reach the enseraphim from the furthest point of the local universe to the capital, Salvington, will be approximately 533, 680 and 607 years respectively, and the mean times will be approximately 400, 407 and 423 years respectively.
¶ The Milky Way and Orvonton
It is difficult to know precisely what the dimensions of the Milky Way are. It is known that it is made up of three elements: the disc, the bulb and the halo. The bulge is the roughly elliptical central core that extends about 8,000 light-years around the galactic center and is about 30,000 light-years thick. The disc is the flattest area that surrounds the bulb and is formed, it is believed, by spiral arms. Our galaxy also has a halo around it, a kind of gigantic envelope in the shape of a flattened sphere, apparently made up of some stars, gas clouds and dark matter.
There are undoubtedly habitable planets on the disk; in the bulge, there is supposed to be a black hole, so it is difficult to know if it has conditions favorable to the existence of habitable planets. It seems certain to me that there are habitable planets in the halo.
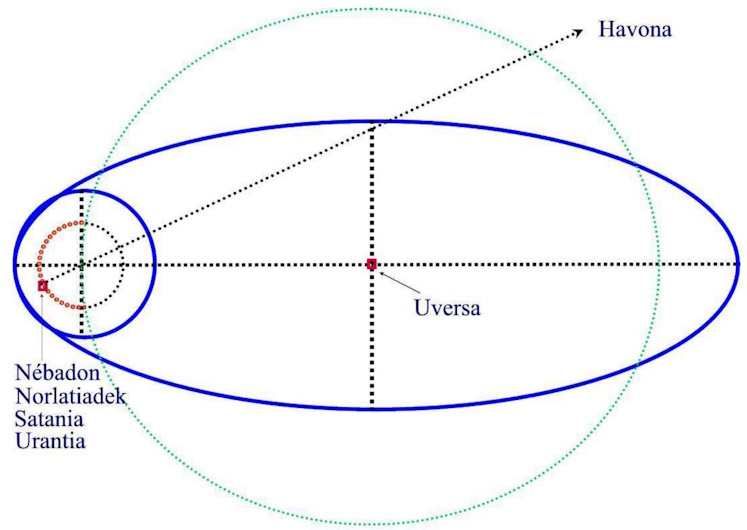
In UB 15:3.1 the Milky Way is said to represent the central core of Orvonton. Therefore it is clear that in addition to the Milky Way, Orvonton has other galaxies and stars. I do not think that “central” should be understood as meaning that the Milky Way is in the center of Orvonton (central position which is incompatible with the distances indicated in paragraph UB 32:2.11), and “central” also means “essential”, “main” or “fundamental”. As UB 32:2.11 suggests, I believe the Milky Way occupies one end of Orvonton (the Milky Way is 100,000 light-years across and Orvonton 500,000 light-years across; from Jerusem to the physical center of Orvonton is 200,000 light years; Satania is on the periphery of Nebadon and Nebadon is near the edge of Orvonton).
To know which part of Orvonton is the Milky Way, it is necessary to estimate how many local universes the galaxy can contain based on its volume and the volume of a local universe. The volume of a local universe has been estimated with an approximation, in my opinion, considerable, having been deduced from a clear indication of the density of suns in space. Estimating the volume of the Milky Way is more complicated and the approximation will be much worse. Just for the purpose of giving a rough approximation of how much of Orvonton our Milky Way is, I will calculate its volume assuming it to be a disk 50,000 light-years in radius and 18,000 light-years in average thickness, without bulge or halo. It is actually a very rough approximation to calculate the number of universes by applying the density of suns in this area of the Milky Way to the entire disk, knowing that this density can be very different in other areas of the galactic disk and especially in the bulge. central or close to it, and knowing that it is possible that peripheral universes (like ours?) occupy adjacent areas belonging to the halo. The resulting volume is 141,371,669,400,000 cubic light years while that of a local universe is 17,576,000,000 cubic light years. The relationship between the two is 8,043. The Milky Way would therefore have about eight thousand local universes out of the hundred thousand of a superuniverse, that is, it would be 8 percent of Orvonton.
With this approximate calculation I venture the hypothesis that the Milky Way is one of the ten largest sectors of Orvonton, specifically the fifth, whose capital is Umayor fifth (UB 15:14.7). If we add the assumption that Orvonton is a huge ellipse with the same average thickness as the Milky Way (18,000 light years) and we remember that the major axis of this ellipse is 500,000 light years (UB 32:2.11) we will calculate, knowing that Orvonton’s total volume must be 10 times that of the Milky Way, whose minor axis will be 200,000 light years.
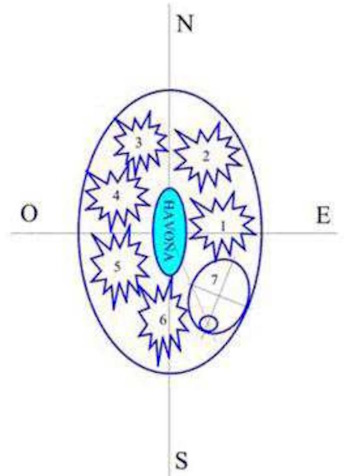
Figure 1 represents an approximate scale of an ellipse with a 500,000 light-year major axis and a 200,000 minor axis, at one end of which is the Milky Way, 100,000 light-years in diameter. The justification for this extreme location of the Milky Way has been noted before. The circumference of the points located 200,000 light years from the physical center of the superuniverse has been drawn in green, and within the Milky Way a centered circumference of radius 30,000 light years, which is the distance from the Sun to its center. On this circumference, points that are more than 200,000 light years from the physical center of Orvonton have been marked in red. Our system must be in the area corresponding to one of these points marked in red. Figure 2 represents the spatial level of the superuniverses as defined by paragraph UB 15:1.4. This distribution justifies the direction toward Havona indicated in Figure 1, and paragraph 167:19 justifies the position of our system on the circumference of 30,000 light-years in radius.
Contemplating figure 1, it could be deduced that the volume of Orvonton that is outside the Milky Way is occupied by stellar groups and systems smaller than the Milky Way, which would justify considering it the “central nucleus” of the superuniverse as it is a very large star system compared to the others in Orvonton. In any case, these other smaller systems must have a distribution that allows, together with the Milky Way, to recognize “immediately the ten largest sectors of the seventh galaxy” (UB 15:3.4).
¶ Conclusions
The paragraph UB 41:3.2 is a clear indication about the density of suns in the space of our local universe —and probably of other local universes of the Milky Way— which, together with other data from the Urantia Book, allows us to estimate the volume of Satania and Nebadon.
With some additional assumptions, the average distance between stars in this zone of creation, and the order of magnitude of the distances in Satania and Nebadon, have been estimated.
Assuming certain assumptions about the dimensions of the Milky Way, and for the purposes of a first rough approximation, it has been estimated that our galaxy may have 8% of the local universes of Orvonton, and although this figure may vary when the dimensions are better known of the Milky Way, the hypothesis is ventured that the Milky Way is the fifth major sector of Orvonton. Based on other information from the UB, the Milky Way is located at one end of the superuniverse and our planet is positioned within both star systems.