Auteur : Sir James Jeans, MA, D. Sc., Sc. D., LL. D., FRS
[ p. 194 ] Nous avons commenté le vide surprenant de l’espace : six grains de poussière dans la gare de Waterloo représentent à peu près la mesure dans laquelle elle est occupée par des étoiles dans ses parties les plus encombrées. Le commentaire aurait bien pu prendre une autre forme. Six grains de poussière contiennent, disons, un milliard de milliards de molécules. Notre modèle de l’espace est vide parce que ce grand nombre de molécules se trouve être agrégé en seulement six morceaux. Dans l’espace réel, l’unité d’agrégation est l’étoile, et une étoile moyenne contient environ 1056 molécules — un nombre si grand qu’il est tout à fait inutile d’essayer de l’imaginer. Le vide de l’espace ne provient pas d’une pénurie de molécules ; Cela vient du fait que, hormis celles qui forment les nuages de gaz ténus qui s’étendent d’étoile en étoile, les molécules sont regroupées en d’immenses colonies que nous appelons étoiles, comptant chacune environ 1056 membres. Pourquoi les molécules de l’espace se regrouperaient-elles ainsi, alors que celles des pièces où j’écris et où vous lisez ne le font pas ?
En suivant une méthode scientifique éprouvée, nous pouvons tenter de découvrir pourquoi ces agrégats se sont formés, en examinant d’abord ce qui les maintient ensemble maintenant qu’ils sont formés. L’atmosphère terrestre est composée d’environ 1041 molécules. Pourquoi restent-elles comprimées dans l’atmosphère au lieu de se disperser dans l’espace ? La réponse est bien sûr fournie par la gravitation terrestre. Une balle tirée depuis la surface terrestre à une vitesse de 11,2 km/s ou plus s’envolera dans l’espace, car l’attraction terrestre est [ p. 195 ] insuffisante pour la retenir lorsqu’elle se déplace à une telle vitesse. Mais une balle tirée à une vitesse inférieure à 11,2 km/s ne quitte pas la Terre ; sa vitesse est insuffisante pour la soustraire à l’attraction terrestre. Ainsi, les molécules-balles qui forment l’atmosphère terrestre, volant à une vitesse inférieure à 400 mètres par seconde, n’ont aucune chance de s’échapper. La gravitation terrestre les attire continuellement vers la Terre, de sorte que celle-ci conserve son enveloppe d’air.
À de rares intervalles, une molécule peut connaître une succession de collisions exceptionnellement heureuses avec d’autres molécules, atteignant ainsi une vitesse de plus de 11,1 km/s. Une molécule qui atteint l’extérieur de l’atmosphère terrestre à une telle vitesse la quittera complètement et rejoindra la foule interstellaire des molécules errantes. La Terre perd ainsi continuellement son atmosphère, mais les calculs montrent que cette perte, même en millions de millions d’années, est tout à fait insignifiante, de sorte que nous pouvons considérer l’atmosphère terrestre comme permanente.
Il en va de même pour le Soleil. La chaleur du Soleil a décomposé les molécules de son atmosphère en atomes qui les constituent, et ceux-ci se déplacent à une vitesse moyenne d’environ 3 kilomètres par seconde. Or, une balle atomique devrait se déplacer à environ 610 kilomètres par seconde pour s’échapper complètement du Soleil, de sorte que les atomes solaires subsistent et forment une atmosphère.
Si toutes les molécules d’air d’une pièce ordinaire étaient rassemblées en un seul bloc au centre de la pièce, la boule d’air ainsi formée exercerait bien sûr une attraction gravitationnelle sur ses molécules les plus externes, du même type que la Terre et le Soleil exercent sur les molécules de leurs atmosphères. Mais, comme le poids de cette boule d’air est si faible, l’intensité de son attraction gravitationnelle [ p. 196 ] serait également faible ; elle serait même si faible qu’une vitesse d’environ un mètre par siècle suffirait à en détacher les molécules les plus externes. Comme les molécules d’air ordinaire se déplacent à environ 500 mètres par seconde, une telle boule d’air se disperserait immédiatement dans toute la pièce. En revanche, si la pièce était assez grande pour contenir le Soleil, toutes ses molécules pourraient rester en boule au centre, comme elles le font dans le Soleil. Les molécules les plus externes auraient besoin d’une vitesse d’au moins 610 kilomètres par seconde pour s’échapper, de sorte que leurs vitesses réelles d’environ 450 mètres par seconde ne leur seraient d’aucune utilité.
Atmosphères planétaires. En général, la question de l’échappement ou non dépend de l’issue d’une bataille entre les vitesses moléculaires des molécules les plus externes et l’intensité de l’emprise gravitationnelle que le reste de la masse exerce sur elles. Le système solaire en fournit de nombreux exemples. La Lune n’a qu’un sixième de l’emprise gravitationnelle sur les molécules d’une atmosphère que la Terre, de sorte que toute atmosphère qu’elle aurait pu avoir s’est déjà échappée. Mercure a les deux cinquièmes de l’emprise gravitationnelle de la Terre, mais, en raison de sa proximité avec le Soleil, sa surface tournée vers le Soleil est très chaude, ce qui a pour conséquence que son atmosphère s’est également échappée. L’emprise gravitationnelle de Mars sur ses molécules n’est que d’un cinquième de celle de la Terre, mais sa surface est plus froide. Les calculs montrent que la vapeur d’eau et les molécules plus lourdes devraient rester, tandis que les molécules plus légères d’hélium et d’hydrogène devraient s’être échappées. C’est probablement ce qui s’est réellement produit. Le plus gros satellite de Saturne et les deux plus gros satellites de Jupiter exerceraient à peu près la même emprise gravitationnelle que la Lune, mais comme leurs surfaces doivent être énormément plus froides que celle de la Lune, ils devraient pouvoir conserver une atmosphère. Certains observateurs affirment avoir observé des signes d’atmosphère sur les trois satellites. Les quatre planètes principales exercent une emprise gravitationnelle plus forte sur leurs molécules que la Terre et conservent donc facilement leur atmosphère, tandis que Vénus, avec une emprise gravitationnelle approximativement identique à celle de la Terre, conserve également une atmosphère.
Ces considérations expliquent amplement pourquoi les molécules des étoiles doivent nécessairement rester agrégées maintenant que les agrégats se sont formés, mais la question de savoir comment et pourquoi ces agrégats se sont formés est bien plus complexe. Qu’est-ce qui, par exemple, a déterminé qu’il devait y avoir environ 1056 molécules dans chaque étoile plutôt que 1054 ou 1058 ?
¶ Instabilité gravitationnelle
Il est naturel de se demander si les forces qui maintiennent aujourd’hui une étoile ensemble ne seraient pas également responsables de sa chute initiale. Cela nous amène à étudier en détail le pouvoir d’agrégation de la gravitation.
Cinq ans après que Newton eut publié sa loi de la gravitation, Bentley, le maître du Trinity College, lui écrivit, soulevant la question de savoir si la force de gravitation nouvellement découverte n’expliquerait pas l’agrégation de la matière en étoiles, et nous trouvons Newton répondant, dans une lettre datée du 10 décembre 1692 :
Il me semble que si la matière de notre soleil et de nos planètes, et toute la matière de l’univers, étaient uniformément dispersées dans tous les cieux, et que chaque particule avait une gravité innée envers toutes les autres, et que tout l’espace dans lequel cette matière est dispersée était fini, la matière à l’extérieur de cet espace tendrait par sa gravité [ p. 198 ] vers toute la matière à l’intérieur, et par conséquent tomberait au milieu de tout l’espace, et y composerait une grande masse sphérique. Mais si la matière était uniformément disposée dans un espace infini, elle ne pourrait jamais se rassembler en une seule masse ; mais une partie se rassemblerait en une masse et une autre en une autre, de manière à former un nombre infini de grandes masses, dispersées à de grandes distances les unes des autres dans tout cet espace infini. Et c’est ainsi que le soleil et les étoiles fixes pourraient être formés, en supposant que la matière soit de nature lucide.
Une étude mathématique précise que j’ai entreprise en 1901 confirme non seulement la conjecture de Newton en termes généraux, mais fournit également une méthode pour calculer la taille des agrégats qui se formeraient sous l’action de la gravitation.
La Formation des Condensations. Vous vous tenez au milieu d’une pièce et frappez des mains. En langage courant, vous faites du bruit ; le physicien, dans son domaine professionnel, dirait que vous créez des ondes sonores. À mesure qu’elles se rapprochent, vos mains expulsent les molécules d’air intermédiaires. Celles-ci se précipitent, entrant en collision avec les molécules des couches d’air externes, qui sont à leur tour chassées pour entrer en collision avec des couches encore plus éloignées ; la perturbation initialement créée par le mouvement de vos mains se propage sous forme d’onde. Bien que les molécules individuelles aient une vitesse moyenne de 500 yards par seconde, le zigzag de leurs mouvements réduit la vitesse de la perturbation, comme nous l’avons déjà vu, à environ 370 yards par seconde – la vitesse ordinaire du son. À mesure que la perturbation atteint un point, le nombre de molécules y devient anormalement élevé, car les molécules en mouvement s’ajoutent au quota normal de molécules à ce point. Cela produit bien sûr un excès de pression. C’est cette surpression agissant sur [ p. 199 ] mon tympan qui transmet une sensation à mon cerveau, de sorte que j’entends le bruit de vos battements de mains.
Cet excès de pression ne peut évidemment pas persister longtemps, de sorte que l’excès de molécules qui le produit doit se dissiper rapidement. C’est ainsi que l’onde se propage. Pourtant, un facteur s’oppose à sa dissipation. Chaque molécule exerce une attraction gravitationnelle sur toutes ses voisines, de sorte qu’un excès de molécules entraîne également un excès de force gravitationnelle. Dans une onde sonore ordinaire, cette force est absolument insignifiante, mais telle quelle, elle exerce une force infime qui retient les molécules et les empêche de se disperser aussi librement qu’elles le feraient autrement. Lorsque le même phénomène se produit à l’échelle astronomique, les forces correspondantes peuvent prendre une importance écrasante.
Considérons le gaz présent dans toute région de l’espace où le nombre de molécules est supérieur à la moyenne de l’espace environnant comme une « condensation ». On peut alors démontrer que, si une condensation est suffisamment étendue, l’excès de force gravitationnelle peut suffire à inhiber complètement la diffusion. Dans ce cas, la condensation peut croître continuellement en attirant des molécules extérieures, dont les vitesses moléculaires sont alors insuffisantes pour les éloigner.
Que cela se produise ou non dépendra bien sûr de la vitesse du mouvement moléculaire dans le gaz, ainsi que de l’ampleur de la condensation. Mais cela ne dépendra absolument pas de l’ampleur du processus de condensation. En doublant le nombre excédentaire de molécules dans une condensation, on double l’ampleur de la condensation. Ce faisant, on double l’attraction gravitationnelle qui tend à accroître la condensation, mais on double également la surpression [ p. 200 ] qui tend à la dissiper ; on double les poids de chaque côté de la balance, mais celle-ci oscille toujours dans le même sens. Si les conditions sont favorables à sa croissance, une condensation continue automatiquement de croître jusqu’à ce qu’il ne reste plus de molécules à absorber.
Plus une condensation est étendue dans l’espace, plus les conditions sont favorables à sa croissance continue. Toutes choses égales par ailleurs, une condensation de trois millions de kilomètres de diamètre exercera une force gravitationnelle deux fois supérieure à celle d’une condensation d’un million de kilomètres de diamètre, mais les surpressions sont les mêmes dans les deux cas. Ainsi, plus une condensation est grande, plus elle a de chances de croître, et en imaginant des condensations de plus en plus grandes, nous devons finalement arriver à des condensations d’une taille telle qu’elles sont vouées à continuer de croître. La loi de la nature est ici celle de la concurrence sans restriction. Rien ne réussit mieux que le succès, et nous constatons donc que les condensations initialement importantes ont la capacité de croître encore davantage, tandis que les petites se dissipent simplement.
Supposons maintenant qu’une énorme masse de gaz uniforme s’étende dans l’espace sur des millions de millions de kilomètres dans toutes les directions. Toute perturbation qui perturbe son uniformité peut être considérée comme créant des condensations de toutes tailles imaginables.
Cela peut ne pas paraître évident à première vue ; on pourrait penser qu’une perturbation qui n’affecterait qu’une petite zone de gaz ne produirait qu’une condensation de faible étendue. Un tel argument néglige la manière dont l’attraction gravitationnelle d’un petit corps agit dans tout l’univers. La Lune provoque des marées sur la Terre lointaine, et des marées aussi, bien qu’incomparablement moindres, sur les étoiles les plus lointaines. Chaque fois que [ p. 201 ] l’enfant jette son jouet hors de sa poussette, il perturbe le mouvement de toutes les étoiles de l’univers. Tant que la gravitation agit, aucune perturbation ne peut être confinée à une zone inférieure à l’espace entier. Plus la perturbation qui les crée est violente, plus les condensations seront intenses au départ, mais même la plus petite perturbation doit provoquer des condensations, même si celles-ci peuvent être d’une intensité extrêmement faible. Et nous avons vu que le sort d’une condensation n’est pas déterminé par son intensité, mais par sa taille. Aussi faible que soit leur intensité initiale, les grandes condensations continuent de croître, tandis que les petites disparaissent. Avec le temps, il ne reste plus qu’un ensemble de grandes condensations. L’analyse mathématique déjà mentionnée montre qu’il existe une masse minimale définie telle que toutes les condensations inférieures à cette masse se dissipent dans l’espace. Avec une approximation suffisante pour notre propos, cette masse minimale est telle que si un dixième de cette masse de gaz était isolé dans l’espace et que tout le reste du gaz était annihilé, les molécules ne parviendraient de justesse à s’échapper de sa surface[1].
On peut dire que la masse de gaz originelle uniformément répartie était « instable » parce que toute perturbation, [ p. 202 ] si légère soit-elle, la faisait changer entièrement de configuration ; elle avait les attributs dynamiques d’un bâton en équilibre sur sa pointe, ou d’une bulle de savon prête à éclater.
Chaos primitif. Ces résultats théoriques généraux peuvent désormais s’appliquer à n’importe quelle masse de gaz. Commençons par les appliquer à l’hypothèse newtonienne de « matière uniformément répartie dans un espace infini ». Nous remontons en imagination à une époque où toute la substance des étoiles et des nébuleuses actuelles était uniformément répartie dans l’espace ; en bref, nous partons du chaos primitif, d’où sont issues la plupart des théories scientifiques de la cosmogonie. Hubble a estimé que si toute la matière des parties de l’univers que nous connaissons était redistribuée uniformément dans l’espace, le gaz ainsi formé n’aurait qu’environ 1,5 x 10-31 fois la densité de l’eau. Cette estimation est presque certainement sous-estimée, même si elle représente les conditions actuelles, et pour tenter de reconstituer le gaz primitif, nous devons ajouter quelque chose pour tenir compte des molécules et des atomes qui ont fondu en radiations entre-temps. Dans l’ensemble, une densité de 10-30 n’est peut-être pas déraisonnable à attribuer à l’hypothétique nébuleuse primitive. Elle est presque inconcevablement basse. Dans l’air ordinaire, à une densité d’un huit-centième de celle de l’eau, la distance moyenne entre molécules adjacentes est d’environ un huit-millionième de pouce ; dans le gaz primitif que nous étudions maintenant, la distance correspondante est de deux ou trois mètres. Ce contraste nous ramène à nouveau au thème de l’extrême vide de l’espace.
Quel est le poids minimum de condensation qui persisterait dans ce gaz primitif ?
Le calcul montre que si l’air ordinaire était atténué [ p. 203 ] à ce degré extraordinaire, aucune condensation ne pourrait persister et continuer à croître à moins d’avoir au moins 62 millions et demi de fois le poids du soleil ; tout poids de gaz plus petit exercerait une attraction gravitationnelle si légère sur ses molécules les plus externes, que leurs vitesses moléculaires normales de 500 mètres par seconde conduiraient à la dissipation rapide de toute la condensation.
Des calculs similaires peuvent être effectués en se référant à d’autres densités de gaz et vitesses moléculaires supposées. Le tableau suivant indique les poids des condensations qui se formeraient dans des masses primitives de gaz chaotique ayant les densités indiquées dans la première colonne et les différentes vitesses moléculaires mentionnées en haut des colonnes suivantes. Dans chaque cas, les poids des condensations sont exprimés en fonction du poids du Soleil :
Masse volumique en termes d’eau | Vitesse molaire de 500 yards par seconde | Vitesse molaire de 1 000 yards par seconde | Vitesse molaire de 2 000 yards par seconde | Vitesse molaire de 3 000 yards par seconde
— | — : | — : | — : | — :
10-29 | 25 000 000 | 200 000 000 | 1 500 000 000 | 5 000 000 000
10-30 | 62 500 000 | 500 000 000 | 4 000 000 000 | 13 000 000 000
1,5 x l0-31 | 100 000 000 | 1 300 000 000 | 10 000 000 000 | 30 000 000 000
Toutes les étoiles connues ont un poids comparable à celui du Soleil. Ainsi, si, comme l’a conjecturé Newton, les étoiles sont d’abord apparues par des condensations de ce type, les valeurs de ce tableau devraient être comparables à l’unité. La conjecture de Newton, telle que nous venons de l’examiner, est manifestement intenable, car tous les poids calculés sont des millions de fois supérieurs à celui du Soleil. Si un chaos primitif tel que celui que nous étudions actuellement avait jamais existé, il ne se condenserait pas en étoiles, mais en condensations considérablement plus massives, chacune ayant le poids de millions d’étoiles.
[ p. 204 ]
¶ La Naissance des Grandes Nébuleuses
Il est significatif que l’on connaisse dans l’espace des corps dont le poids est égal à celui qui vient d’être calculé, à savoir les grandes nébuleuses extragalactiques. Deux nébuleuses ont un poids assez précis : la Grande Nébuleuse d’Andromède (Planche IV, p. 30) et la nébuleuse NGC 4594 de la Vierge (Planche XV). Hubble estime ces poids comme suit :
| Nébuleuse | Poids |
|---|---|
| Nébuleuse M 31 | poids = 3 500 millions de fois celui du Soleil |
| Nébuleuse NGC 4594 | „ = 2000 |
Ces estimations sont probablement toutes deux basses, mais leur ordre de grandeur général suggère que les condensations initialement formées à partir de la nébuleuse primitive devaient être les grandes nébuleuses extragalactiques, et non de simples étoiles. Bien sûr, la formation des grandes nébuleuses de cette manière n’est, au mieux, qu’une conjecture – ne serait-ce que parce que nous ne pouvons jamais savoir si l’hypothétique nébuleuse primitive a même existé – mais cela semble l’hypothèse la plus raisonnable que nous puissions formuler pour expliquer l’existence des nébuleuses actuelles. Ces nébuleuses sont si généralement similaires les unes aux autres qu’il semble probable qu’elles aient toutes été produites par l’action du même agent, et ce que nous venons d’examiner fournit une explication raisonnable qui, outre l’existence postulée de la nébuleuse primitive continue, repose sur de véritables causes.
Les grandes nébuleuses ne sont bien sûr pas exactement similaires, et notre prochaine enquête doit porter sur l’origine de leurs différences.
Si les condensations de la nébuleuse gazeuse primitive [ p. 205 ] s’étaient formées et contractées de manière absolument régulière, le produit final aurait été un réseau de masses de gaz parfaitement égales et semblables, espacées avec une régularité parfaite. Mais la nature est rarement aussi régulière ; et il n’y a pas lieu de s’étonner que le réseau nébulaire observé ne soit pas uniformément espacé, ou que ses membres ne soient ni de poids égaux, ni disposés symétriquement. En se contractant, les condensations originelles du gaz primitif ont dû produire des courants, et ceux-ci ne sont guère susceptibles de se produire de manière absolument symétrique. Si le mouvement de chaque masse de gaz en condensation avait été directement dirigé vers le centre de la condensation en tout point, le résultat final aurait été une nébuleuse sphérique dépourvue de tout mouvement, mais tout système de courants moins symétrique aurait donné une rotation à chaque masse en contraction. Cette rotation serait sans doute très lente au début, mais le principe bien connu de « conservation du moment angulaire » exige que, lorsqu’un corps en rotation se contracte, sa vitesse de rotation augmente. Ainsi, une fois le processus de condensation terminé, le produit final serait une série de nébuleuses tournant à des vitesses différentes.

Rotation des nébuleuses. Et c’est exactement ce que l’on observe ; d’après nos données, les nébuleuses sont en rotation, et à des vitesses différentes. Les différentes parties de la surface de toute masse en rotation ont nécessairement des vitesses différentes dans l’espace. Le Soleil, par exemple, tourne autour de son axe dans une direction telle que la surface que nous voyons se déplace toujours d’est en ouest ; de ce fait, le bord oriental avance toujours vers la Terre, tandis que le bord occidental s’éloigne de nous. Un spectroscope braqué successivement sur différentes parties de la surface du Soleil révèle immédiatement ces différences de vitesse ; elles nous assurent non seulement de la rotation du Soleil, [ p. 206 ], mais nous permettent d’en mesurer l’ampleur. Les nébuleuses peuvent être examinées de la même manière, et l’examen montre qu’un grand nombre d’entre elles tournent avec le mouvement parfaitement régulier d’un corps solide – une toupie, par exemple. Mesurées selon les normes terrestres, leurs vitesses de rotation semblent extraordinairement lentes ; par exemple, la Grande Nébuleuse M 31 d’Andromède met environ 19 000 000 d’années pour effectuer une rotation complète, mais cette lenteur apparente est une conséquence inévitable de la taille gigantesque de la nébuleuse. Même pour effectuer un tour complet en 19 000 000 d’années, les parties extérieures de la nébuleuse doivent se déplacer à des vitesses de plusieurs centaines de kilomètres par seconde.
Quelques nébuleuses présentent des formes assez irrégulières, mais la majorité ont des formes régulières. Il est très significatif que ce soient précisément les formes que, mathématiquement, on peut calculer, présenteraient des masses de gaz en rotation. En réalité, il existe un argument bien plus convaincant pour supposer que les nébuleuses sont des masses de gaz en rotation. À partir de données purement observationnelles sur la brillance de surface et d’autres caractéristiques, Hubble a découvert que la quasi-totalité de ces nébuleuses pouvaient être disposées selon une séquence linéaire unique – elles pouvaient être disposées dans l’ordre, comme des perles sur un fil. Et cet ordre s’est avéré pratiquement identique à la séquence précédemment calculée, par des méthodes purement théoriques, pour les configurations de masses de gaz en rotation à des vitesses progressivement croissantes.
Examinons cette séquence de configurations théoriques dans leur ordre naturel.
Une masse de gaz immobile en rotation prendrait naturellement une forme sphérique sous l’effet de sa propre gravitation. On connaît un certain nombre de nébuleuses parfaitement sphériques ; un exemple typique est présenté à la fig. 1 de la planche XVI.

Sous une légère rotation, la masse prend la forme d’une orange légèrement aplatie, comme la Terre ou Jupiter. On connaît également de nombreuses nébuleuses de cette forme ; un exemple est présenté à la figure 2 de la même planche.
Avec un degré de rotation plus élevé, le degré d’aplatissement augmente, mais les calculs théoriques montrent que la forme orange disparaît rapidement. L’équateur commence par présenter un renflement prononcé, qui, avec une rotation suffisante, se transforme en une arête vive, la masse en rotation prenant alors la forme d’une lentille biconvexe. Cette prédiction théorique est amplement confirmée par l’observation : un grand nombre de ces nébuleuses en forme de lentille sont observées dans le ciel. Un exemple est présenté à la figure 3 de la Planche XVI.
L’étape suivante est assez sensationnelle. Contrairement à ce que l’on pourrait croire, une rotation plus poussée n’entraîne pas un aplatissement supplémentaire. Jusqu’à présent, chaque augmentation de rotation a accentué le renflement de l’équateur, mais celui-ci est désormais aussi prononcé que possible. La théorie montre que l’aplatissement a également atteint sa limite extrême et que l’étape suivante consistera en une éjection de matière par le bord tranchant de l’équateur et une dispersion sur tout le plan équatorial. Ici encore, l’observation confirme la théorie ; les figures 4 et 5 (Planche XVI) montrent des types de nébuleuses réellement observées, la première étant la nébuleuse de la Vierge dont nous avons déjà parlé.
La couche de gaz relativement mince qui se trouve actuellement dans le plan équatorial est similaire, au moins sur un point, à la matière de Newton « répartie uniformément dans un espace infini ». Des perturbations peuvent s’y produire de diverses manières, et toute perturbation, aussi légère soit-elle, doit entraîner la création d’une série de condensations. Comme précédemment, celles dont la taille est inférieure à une certaine limite disparaissent d’elles-mêmes, tandis que celles dont la taille est supérieure augmentent continuellement en intensité jusqu’à avoir absorbé tout le gaz du plan équatorial. De nouveau, comme pour l’hypothétique chaos primitif, nous pouvons calculer la taille minimale de condensation dont on peut s’attendre à ce qu’elle ait une existence permanente, et une fois de plus le résultat s’avère hautement significatif.
Les estimations de Hubble concernant le poids total de deux nébuleuses remarquables ont déjà été présentées. Les distances, et donc les tailles, de ces deux nébuleuses étant connues, il est facile de calculer la densité moyenne du gaz dans toute la nébuleuse. La densité moyenne de M 31 est d’environ 5 x 10-22 de celle de l’eau ; le chiffre correspondant pour NGC 4594 est de 2 x 10-21. Ces chiffres nous donnent une idée de la densité de matière dans les régions externes des nébuleuses. Bien que ces densités soient environ un milliard de fois supérieures à la densité estimée de la nébuleuse primitive de l’espace, elles restent presque incroyablement basses. Il n’y a encore qu’environ une molécule par pouce cube, et un seul souffle des poumons d’une mouche pourrait remplir une grande cathédrale d’air de cette densité.
En calculant les poids des plus petites condensations susceptibles de se former et de persister dans un gaz de cette faible densité, nous obtenons les résultats présentés dans le tableau suivant. Les vitesses moléculaires sont considérées comme assez faibles, afin de tenir compte du refroidissement qui doit se produire lorsque le gaz s’étend dans le plan équatorial de la nébuleuse.
De nouveau, les poids des condensations sont exprimés en termes de poids du Soleil. Il est important de noter que la plupart des entrées du tableau représentent des poids comparables à celui du Soleil. Il s’agit enfin de poids stellaires ; les condensations qui doivent se former dans les régions extérieures des grandes nébuleuses auront des poids comparables à ceux des étoiles.
| Masse volumique en termes d’eau | Vitesse molaire de 100 yards par seconde | Vitesse molaire de 300 yards par seconde | Vitesse molaire de 500 yards par seconde |
|---|---|---|---|
| 10-21 | 1,7 | 36 | 220 |
| 10^-22 ^ | 5 | 130 | 625 |
| l0-23 | 17 | 360 | 2200 |
¶ La Naissance des Étoiles
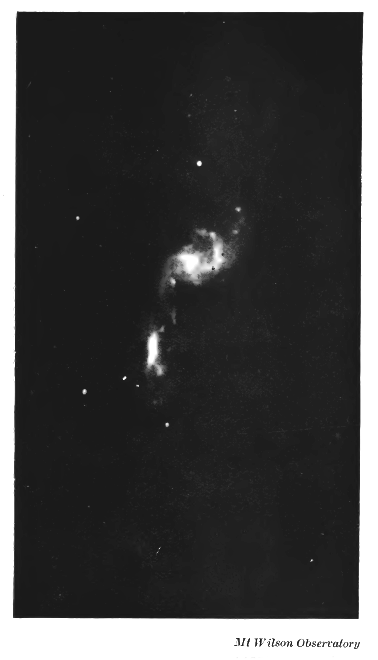
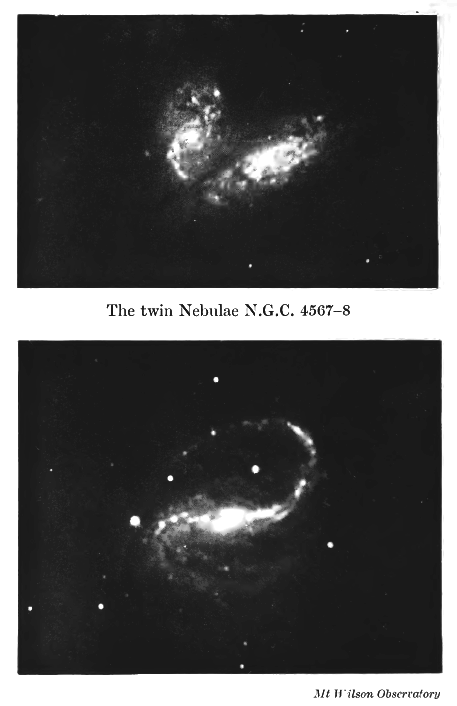
Et il ne fait aucun doute que le processus que nous venons d’examiner est celui de la naissance des étoiles. Un simple coup d’œil aux photographies de nébuleuses suffit à démontrer que la matière éjectée dans le plan équatorial d’une nébuleuse ne s’y répartit pas uniformément ; on la voit tomber en amas, nœuds ou condensations. Ces phénomènes sont assez apparents sur de nombreuses photographies de nébuleuses déjà présentées, mais ils sont encore plus visibles dans les nébuleuses observées presque en entier, comme par exemple les deux nébuleuses remarquables représentées sur les planches [XVII] (#Universe_plate_17) et [XVIII] (#Universe_plate_18).
Ces amas sont invariablement trop grands pour être interprétés comme des étoiles isolées ; il s’agit plus probablement de groupes d’étoiles. Dans les plus grands télescopes, ils se fragmentent en un grand nombre de points lumineux, comme déjà exposé dans la planche XI (p. 70). Nous avons déjà mentionné les raisons qui nous poussent à considérer ces points lumineux comme de véritables étoiles, la principale étant que certains d’entre eux présentent les fluctuations lumineuses caractéristiques [ p. 210 ] des variables Céphéides. On ne sait pas exactement si les étoiles se forment directement par condensation dans le plan équatorial de la nébuleuse, ou si de plus grandes condensations se forment d’abord, à savoir les amas observables sur les photographies nébuleuses, qui forment ensuite des condensations plus petites, les étoiles. Globalement, il semble probable que deux processus soient impliqués : d’abord la fragmentation de la matière nébulaire en grandes condensations, puis la fragmentation de ces grandes condensations en étoiles. Une telle succession de processus pourrait bien accompagner un refroidissement progressif de la situation, et il est bien sûr possible que plus de deux processus soient en jeu. Il n’est pas nécessaire de se forger une opinion définitive à ce sujet pour le moment, car cela n’est en aucun cas essentiel à la progression du débat principal.
Une collection de photographies nébuleuses nous permet de suivre l’évolution nébulaire depuis les premiers stades, illustrés par la Planche XVI (p. 207), en passant par la première apparition de paquets granulaires, comme ceux de la Planche XVII, et la première apparition distincte d’étoiles, illustrée par la Planche XVIII, jusqu’aux stades ultérieurs, illustrés par les Planches XIX et XX, où la nébuleuse apparaît comme un simple nuage d’étoiles. Hubble a pu suivre la séquence encore plus loin et a pu tracer une transition continue depuis les nébuleuses de ce dernier type jusqu’aux nuages d’étoiles purs tels que le Grand et le Petit Nuage de Magellan, illustrés par la Planche XXI.
Ainsi, les étoiles semblent être nées de la même manière que nous avons supposé que leurs parents, les grandes nébuleuses, étaient nés avant elles, à savoir par l’effet de ce que l’on appelle généralement « l’instabilité gravitationnelle ». Celle-ci provoque la fragmentation de toute masse de gaz chaotique en condensations détachées, [ p. 211 ] et, plus le gaz originel est ténu, plus le poids des condensations qui en résultent est important. La nébuleuse primitive originelle était d’une densité si faible que les condensations qui s’y formaient pesaient des milliards de fois le poids du Soleil. Celles-ci ont tellement augmenté leur densité en se contractant que, lorsque leur rotation les a fait éjecter de la matière gazeuse, celle-ci s’est condensée en masses de poids stellaire que nous pensons être en réalité des étoiles.


Nous avons une connaissance moins certaine du premier processus que du second. Notre seule raison de penser que le premier a jamais eu lieu est l’existence actuelle des nébuleuses extragalactiques. Rien ne prouve que la nébuleuse chaotique primitive ait jamais existé, si ce n’est que l’hypothèse de son existence antérieure permet d’expliquer de manière très satisfaisante l’existence actuelle des nébuleuses. D’autre part, nous savons non seulement que les étoiles existent, mais aussi que les masses de gaz existent, à partir desquelles la théorie démontre que les étoiles doivent nécessairement naître. Ce sont les franges équatoriales ténues des grandes nébuleuses. Nos télescopes nous montrent à la fois les franges nébuleuses et les étoiles, et nous pouvons presque étudier le processus réel de naissance.
Le système galactique des étoiles. Si tel est le récit exact de la naissance des étoiles, alors notre Soleil et ses compagnons spatiaux doivent être nés d’une nébuleuse en rotation. L’observation corrobore fortement cette conclusion. Depuis l’époque des Herschel, on remarque fréquemment que le système galactique a la forme générale des nébuleuses extragalactiques, le plan galactique représentant bien sûr le plan équatorial de la nébuleuse originelle. Sur des bases purement observationnelles, la pensée astronomique actuelle évolue rapidement vers une vision de l’ensemble du système galactique soit comme une nébuleuse en rotation, soit comme les vestiges d’une nébuleuse. Il est même possible que celle-ci conserve encore une région centrale non encore condensée en étoiles. Dans la direction des constellations du Scorpion et d’Ophiuchus se trouvent des nuages sombres qui peuvent soit voiler le centre du système, soit être le centre lui-même.
En 1904, Kapteyn découvrit que les directions du mouvement des étoiles à proximité du Soleil n’étaient pas distribuées au hasard. Les étoiles semblaient préférer se déplacer dans une direction du plan galactique plutôt que dans d’autres directions – il appelait cela le « streaming stellaire ». Cette particularité du mouvement des étoiles devrait apporter un éclairage sur leur origine.
Chaque étoile se déplace sur une orbite complexe sous l’attraction gravitationnelle de toutes les autres étoiles du système galactique. Il est impossible de calculer cette orbite en détail. L’orbite d’une planète autour du Soleil est facile à calculer car seuls deux corps sont impliqués, la planète et le Soleil. Mais même lorsque seuls trois corps sont impliqués, il est impossible de calculer les orbites que chacun décrit sous l’attraction conjointe des deux autres : c’est le fameux problème des trois corps, qui n’a jamais été résolu. Lorsque, comme dans le système galactique, des milliards d’étoiles sont impliquées, il est naturellement inutile de tenter de calculer l’orbite de chaque étoile ; ce serait aussi futile que de tenter de calculer la trajectoire de chaque molécule dans un gaz.
Pourtant, les mêmes méthodes statistiques qui nous fournissent des informations utiles sur les propriétés d’un gaz peuvent être appliquées à l’étude du mouvement des étoiles. Il y a tellement d’étoiles que nous ne nous soucions pas des individus ; nous les traitons simplement comme une foule. Les traiter individuellement serait comme si la compagnie ferroviaire essayait de prévoir le trafic du Bank Holiday entre Londres et Brighton en prenant en compte les finances, les habitudes et la psychologie de chaque Londonien.


Sans entrer dans les détails individuels, nous pouvons constater que chaque étoile doit décrire une orbite qui, après avoir fait le tour d’une grande partie de la galaxie, revient à un point proche de son point de départ. Les calculs montrent que chaque tour complet doit prendre des centaines de millions d’années. Malgré cela, les étoiles auront généralement effectué plusieurs tours complets depuis l’existence de la Terre, et si nous avons raison de supposer que l’âge des étoiles est de plusieurs millions de millions d’années, chaque étoile a dû faire le tour de la galaxie plusieurs milliers de fois. Nous devrions donc nous attendre à ce que la galaxie ait désormais une forme définie et permanente ; la répartition des étoiles dans ses différentes parties devrait être devenue quasi stable, et les étoiles devraient s’être stabilisées dans un état proche d’un mouvement stationnaire.
Français Les méthodes statistiques d’investigation montrent qu’il n’existe pas un grand nombre d’arrangements possibles pour un système d’étoiles ayant vécu suffisamment longtemps pour atteindre un état stationnaire. Si le système dans son ensemble ne présente aucune rotation, il n’y a qu’un seul arrangement : les étoiles forment une masse globulaire présentant une symétrie parfaite dans toutes les directions. Les amas globulaires observés (Planche IX, p. 63) fournissent de bonnes approximations de ce type de formation, bien que Shapley ait constaté que la majorité d’entre eux ne sont pas de forme absolument sphérique. Si le système dans son ensemble est doté de rotation, les configurations possibles ont toutes une forme symétrique aplatie, comme une pièce de monnaie, une montre ou un biscuit rond — en d’autres termes [ p. 214 ] mots : un système d’étoiles en rotation doit avoir une forme similaire à celle que nous attribuons à la galaxie. De plus, les mouvements de ces étoiles doivent présenter un « flux d’étoiles » du type précisément découvert par Kapteyn.

Ainsi, la forme de la galaxie et les particularités du mouvement de ses étoiles indiquent que le système galactique dans son ensemble doit être en rotation. Et, comme nous l’avons vu (p. 67), les récentes recherches observationnelles d’Oort, Plaskett et d’autres confirment à peu près que la rotation requise par la théorie est un fait réel. Les mouvements des étoiles indiquent que l’ensemble du système galactique tourne à une vitesse variable d’une région à l’autre, soit environ une révolution tous les 230 millions d’années au voisinage du Soleil. Et le moyeu de cette roue gigantesque se trouve coïncider très étroitement avec le point que Shapley avait précédemment fixé comme centre géométrique du système galactique à partir de ses recherches sur la distribution des amas globulaires.
Ainsi, puisque la rotation ne peut être générée à partir de rien, tous les phénomènes concordent pour montrer que le système galactique a dû naître d’un corps en rotation. Nous ne connaissons qu’un seul type de corps astronomique suffisamment grand pour se transformer en système galactique, à savoir les grandes nébuleuses. Comme la plupart d’entre elles sont considérées, et certaines sont connues avec certitude, comme étant en rotation, il semble raisonnable de conclure que le système galactique a dû naître d’une nébuleuse, à moins que sa structure ne soit encore telle que nous devrions encore le décrire comme une nébuleuse si nous l’observions de la grande distance à laquelle nous observons les autres grandes nébuleuses. La période de rotation observée du système galactique, de l’ordre de 230 millions d’années, est [ p. 215 ] est sensiblement plus longue que la période, connue ou suspectée, de n’importe quelle nébuleuse, mais les dimensions du système galactique sont également plus grandes que celles de n’importe quelle nébuleuse connue, et les deux faits sont cohérents. De plus, le nombre d’étoiles dans le système galactique est probablement sensiblement plus élevé que dans n’importe quelle nébuleuse, tout comme le poids total de ces étoiles[2]. Tout cela montre clairement que si la galaxie est, ou a jamais été, l’une des grandes nébuleuses, elle devait être d’une taille et d’un poids inhabituels.
Nous avons vu comment le Soleil et toutes les étoiles perdent continuellement du poids sous l’effet de leur rayonnement. Il s’ensuit que le poids total du système galactique diminue sans cesse et, par conséquent, son emprise gravitationnelle sur les étoiles qui le composent s’affaiblit continuellement. Si cette emprise venait à disparaître soudainement, chaque étoile remplacerait sa trajectoire courbe actuelle par une ligne parfaitement droite, le long de laquelle elle se déplacerait à sa vitesse actuelle, sans être déviée par les forces gravitationnelles des autres étoiles. De sorte que les étoiles qui constituent actuellement le système galactique seraient bientôt dispersées dans tout l’espace. En bref, si l’attraction gravitationnelle des étoiles était soudainement abolie, la galaxie commencerait à s’étendre à grande vitesse.
Bien que cela soit peu probable, l’abolition progressive de l’attraction gravitationnelle des étoiles, à mesure qu’elles transforment leur poids en rayonnement, doit entraîner une expansion lente et continue de la galaxie : les calculs suggèrent que son taux d’expansion actuel doublerait sa taille en environ 30 millions d’années. L’expansion [ p. 216 ] a dû être beaucoup plus rapide dans le passé, lorsque les étoiles étaient pleines de leur vigueur juvénile et gaspillaient leur substance plus généreusement qu’aujourd’hui, de sorte qu’il semble probable que le système galactique était substantiellement plus petit et plus compact dans le passé qu’aujourd’hui, et la nébuleuse originelle probablement plus petite encore.
Nous avons vu comment les étoiles des grandes nébuleuses semblent se regrouper en amas. Les amas globulaires du système galactique pourraient être des amas d’étoiles du même type, restés intacts par d’autres groupes d’étoiles et ayant ainsi pris leur forme globulaire sous leur propre attraction, comme le ferait une masse de gaz. Shapley constate que ces amas se situent quelque peu en dehors du plan galactique ; il semble qu’ils se soient fragmentés ou désorganisés lors de leur traversée de ce plan, où ils rencontreraient d’autres étoiles.
En revanche, les groupes d’étoiles du type généralement décrit comme des amas en mouvement — les Pléiades, les Hyades, les étoiles de la Grande Ourse et une foule d’autres voyageant avec elles dans l’espace — se déplacent généralement dans le plan galactique. Il est fort possible qu’ils représentent les derniers vestiges d’amas globulaires brisés par interaction avec d’autres étoiles, tous, à l’exception des plus massifs, ayant été éliminés de la formation. L’analyse mathématique montre que l’interaction entre les étoiles de ces amas en mouvement et d’autres étoiles du plan galactique donnerait à chaque amas la forme d’un biscuit plat ou d’une montre, d’un diamètre égal à deux fois et demie son épaisseur. Il est significatif que la majorité des amas en mouvement présentent un aplatissement de ce type, dont l’ampleur concorde assez bien avec la valeur calculée. Il est même concevable que le [ p. 217 ] « amas local » entourant le soleil (p. 65) pourraient être les restes d’un tel groupe d’étoiles.
Les mouvements de ces amas peuvent également induire un aplatissement supplémentaire, perpendiculaire à leur mouvement. Certains amas présentent cet aplatissement supplémentaire, l’amas de la Grande Ourse en étant un exemple frappant.
¶ La naissance des systèmes binaires
En examinant la manière dont les nébuleuses pourraient naître du chaos, nous avons remarqué que l’existence de courants dans le milieu primordial conférerait aux nébuleuses résultantes des degrés variables de rotation. Pour la même raison, les enfants des nébuleuses, les étoiles, doivent également être dotés d’une rotation à leur naissance. Il existe une autre raison à cette rotation. Le principe général de « conservation du moment cinétique » exige que la rotation, comme l’énergie, ne puisse disparaître entièrement. Sa quantité totale est conservée, de sorte que lorsqu’une nébuleuse se fragmente en étoiles, la rotation initiale de la nébuleuse doit être conservée dans les rotations des étoiles. Ainsi, les étoiles, dès leur apparition, sont dotées de rotations transmises par leur nébuleuse mère, en plus des rotations résultant des courants créés lors du processus de condensation.
Leur perte continue de poids modifie les conditions physiques des étoiles, et nous verrons dans le chapitre suivant que ce changement implique généralement une diminution du diamètre de l’étoile. Le même principe de « conservation du moment angulaire » exige désormais qu’à mesure qu’une étoile rétrécit, sa vitesse de rotation augmente. En bref, à mesure qu’une étoile vieillit, sa vitesse de rotation augmente.
[ p. 218 ] Or, la rotation était le facteur essentiel de la naissance des étoiles à partir de la nébuleuse mère. Une nébuleuse parfaitement dépourvue de rotation ne se désintégrerait pas, autant que nous le sachions, en étoiles, et cette prédiction théorique semble confirmée par l’observation, puisque les nébuleuses parfaitement sphériques représentées sur la figure 1 de la Planche XVI ne peuvent jamais être résolues en étoiles au télescope. D’autre part, nous avons vu comment les nébuleuses initialement douées de rotation augmentaient continuellement leur vitesse de rotation sous l’effet du rétrécissement, jusqu’à ce que finalement leur rotation les désintègre et produise une famille d’étoiles à partir de chacune d’elles. La question se pose maintenant de savoir si, à mesure que la vitesse de rotation des étoiles augmente, celles-ci sont susceptibles de se désintégrer à leur tour et de produire une troisième génération de corps astronomiques. On pourrait s’attendre à ce que l’analyse mathématique s’applique indifféremment aux corps grands et petits, quelle que soit leur échelle. Or, un examen détaillé du problème montre qu’en réalité, le processus étudié se répéterait et engendrerait à nouveau une nouvelle génération de corps plus petits, si les conditions physiques étaient favorables.
Les conditions physiques, cependant, ne sont pas réunies ; elles échouent certainement sur un point au moins. Bien qu’une étoile en rotation puisse éjecter de la matière gazeuse dans son plan équatorial, le processus se déroulera à une échelle bien plus petite que dans les nébuleuses. On pourrait s’attendre à ce que la matière éjectée forme des condensations comme précédemment, mais les calculs montrent qu’à moins que la vitesse moléculaire ne soit extraordinairement basse, aucune condensation ne peut survivre à moins d’avoir un poids supérieur au poids total de l’étoile ! Cela signifie qu’avec une vitesse moléculaire raisonnable, le gaz éjecté ne formerait aucune condensation. Il se disperserait simplement dans l’espace environnant, formant une atmosphère sans condensation distincte.
Tel est le cours des événements si les étoiles, comme les nébuleuses avant elles, sont traitées comme de pures masses de gaz. Une autre alternative doit cependant être envisagée.
La fission des étoiles liquides. Nous avons vu comment une nébuleuse gazeuse dépourvue de rotation prendrait une forme strictement sphérique sous l’effet de sa propre attraction gravitationnelle, tandis qu’une légère rotation la ferait s’aplatir en une forme orange, comme la Terre. La Terre a également pris cette forme en raison de sa rotation, bien que sa structure interne soit très différente de celle d’une nébuleuse gazeuse.
Une étude mathématique rigoureuse montre que cette forme orange aplatie doit être commune à tous les corps en rotation lente, quelle que soit leur composition interne ; les gaz, les liquides et les corps plastiques la présentent également. Cependant, la forme d’un corps en rotation rapide dépend fortement de sa disposition et de sa constitution internes, étant particulièrement influencée par la concentration du poids du corps près de son centre.
En raison de la forte compressibilité des gaz, cette concentration centrale de poids atteint sa limite extrême dans une masse purement gazeuse. L’extrême opposé est atteint dans une masse de liquide uniforme et incompressible comme l’eau, où il ne peut y avoir de concentration centrale. À mesure qu’une masse de ce type augmente sa vitesse de rotation, la forme orange légèrement aplatie cède simplement la place à une forme orange plus aplatie. La tendance d’une masse gazeuse à former une arête vive autour de l’équateur est totalement absente, et la section transversale de sa figure reste entièrement elliptique. À une vitesse de rotation encore plus élevée, l’équateur perd sa forme circulaire et devient lui aussi elliptique. La figure présente alors trois diamètres inégaux, mais chaque section transversale est strictement elliptique ; la figure est un « ellipsoïde ». Après cela, son diamètre le plus long commence à s’allonger jusqu’à ce que la masse, toujours de forme ellipsoïdale, ait formé une figure en forme de cigare d’une longueur presque trois fois supérieure à son diamètre le plus court.
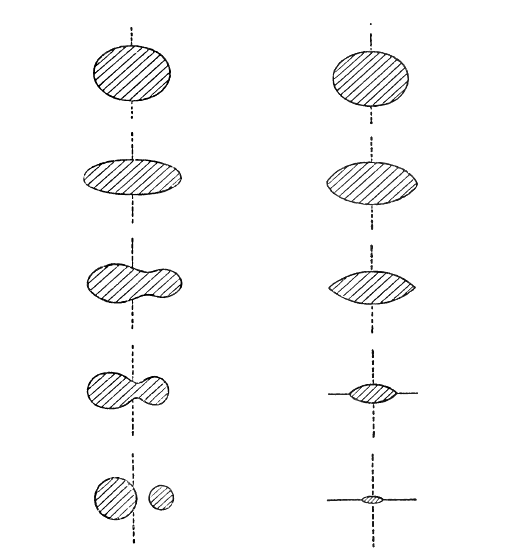
Une nouvelle série d’événements commence alors. La masse liquide se concentre progressivement autour de deux points distincts de son plus grand diamètre, un sillon se formant en son milieu. Ce sillon devient de plus en plus profond jusqu’à diviser le corps en deux masses distinctes, qui tournent alors en orbite l’une autour de l’autre et forment une étoile binaire. La séquence des événements est illustrée à la fig. 11 ; des schémas de l’étape finale, représentés par des étoiles binaires réelles, ont déjà été présentés à la p. 54.
A titre de comparaison, la séquence des formes prises par une masse de gaz en rotation est montrée dans la fig. 12, celle-ci étant identique à la séquence des formes nébuleuses observées qui est effectivement observée, et est illustrée photographiquement dans la Planche XVI (p. 207).
Les deux chaînes de configurations représentées sur les figures 11 et 12 représentent, rappelons-le, les deux cas extrêmes d’un corps en rotation dont la substance est distribuée avec une uniformité complète, et d’un corps en rotation dont la substance est très fortement condensée vers son centre. Comme la constitution des corps astronomiques réels doit se situer quelque part entre ces deux extrêmes, on pourrait naturellement s’attendre à ce qu’un tel corps suive une série de configurations intermédiaires entre les deux représentées sur les figures 11 et 12. La théorie montre qu’en réalité, ce n’est pas le cas. Tous les corps ayant un degré critique de condensation centrale inférieur à un certain [ p. 221 ] suivent la séquence représentée sur la figure 11, ou une séquence qui n’en diffère que légèrement ; tous les corps ayant un degré critique de condensation centrale supérieur suivent la séquence représentée sur la figure 11. 12. Ainsi, lorsque ce degré critique de condensation centrale est atteint, il se produit un [ p. 222 ] basculement brusque de la fig. 11 à la fig. 12. En bref, tout corps en rotation se comporte soit comme s’il était purement liquide, soit comme s’il était purement gazeux ; il n’y a pas de possibilités intermédiaires.
L’astronomie observationnelle ne laisse planer aucun doute sur le fait qu’un grand nombre d’étoiles, peut-être même toutes les étoiles, suivent la séquence illustrée à la figure 11. Aucun autre mécanisme, à notre connaissance, n’explique la formation des nombreux systèmes binaires spectroscopiques, dans lesquels deux constituants décrivent de petites orbites l’un autour de l’autre. Dans ces étoiles, la condensation centrale de masse doit donc être inférieure à la valeur critique mentionnée précédemment ; dans cette mesure, elles se comportent comme des liquides plutôt que comme des gaz.
Nous nous sommes entièrement appuyés sur l’analyse mathématique pour retracer les détails du processus de fission que nous venons de décrire. Et nous sommes totalement incapables de vérifier nos résultats théoriques par l’observation. Il n’existe pas une seule étoile dans le ciel dont nous puissions dire : « Voici une étoile qui a certainement commencé à se briser par fission et qui finira certainement par former un système binaire. » Cela n’est peut-être pas totalement surprenant. Le processus de fragmentation est très probablement de très courte durée comparé à la vie des étoiles, de sorte que, de toute façon, nous devrions étudier un grand nombre d’étoiles avant d’en surprendre une en train de se briser.
D’un autre côté, une étoile en cours de fragmentation devrait être très facilement différenciée des étoiles ordinaires. L’analyse mathématique montre que son intérieur serait dans un état de turbulence considérable, de sorte qu’il serait peu probable qu’elle brille d’une lumière constante : ce serait une étoile « variable ». De plus, son état devrait présenter un changement progressif, bien que la question reste ouverte de savoir si celui-ci serait suffisamment rapide pour être détecté en quelques années d’observation. Enfin, si un groupe ou une classe d’étoiles était suspecté d’être en cours de fission, il devrait être possible de les classer dans un ordre correspondant à l’avancement du processus de fission, et la séquence ainsi formée devrait aboutir à des étoiles dans l’état physique de binaires nouvellement formées.
J’ai récemment suggéré que les Céphéides variables, dont le mécanisme inconnu de variation de la lumière rend de si précieux services à l’astronome, ne sont que des étoiles en cours de fission. Le manque de place nous empêche d’aborder ici la question complexe de savoir dans quelle mesure elles présentent les particularités que l’analyse mathématique exige des étoiles en cours de fission, mais il est facile de constater qu’elles satisfont aux trois tests simples décrits ci-dessus. Ce sont certainement des étoiles variables, et les variations de lumière de différentes étoiles sont si similaires qu’elles suggèrent fortement qu’elles proviennent toutes de la même cause. On soupçonne que les périodes de plusieurs Céphéides changent, et Hertzsprung a estimé que l’étoile prototype, δ Céphées, observée depuis 126 ans, diminue sa période de fluctuation de lumière au rythme d’environ un dixième de seconde par an ; ainsi, un million d’années réduirait sa période actuelle de 5,13 jours de plus d’un jour. Finalement, le Dr Otto Struve a découvert que la séquence des Céphéides correspond presque parfaitement à celle des binaires nouvellement formées. Les perspectives de la « théorie de la fission » des variables céphéides semblent donc prometteuses, mais cette théorie doit être testée de manière approfondie avant d’être acceptée, et on ne peut pas prétendre qu’elle ait été jusqu’à présent testée de manière approfondie ou acceptée de manière exhaustive.
Une autre théorie, initialement proposée par Plummer et Shapley, considère les variables céphéides comme des sphères de gaz pulsées [ p. 224 ]. Le comportement de telles masses de gaz a été étudié mathématiquement par Eddington et d’autres, mais il ne semble pas compatible avec le comportement observé des variables céphéides.
¶ Le développement des systèmes binaires
Quel que soit le processus de formation des systèmes binaires, retracer leur évolution ultérieure est relativement simple. Trois facteurs interviennent simultanément.
Frottement de marée. Le premier de ces trois facteurs, de courte durée, fut appelé « frottement de marée » par Sir George Darwin, qui le premier attira l’attention sur lui et étudia son fonctionnement. Lorsqu’une masse en rotation se brise et forme un système binaire, les deux composantes sont si proches qu’elles soulèvent nécessairement d’énormes marées l’une sur l’autre ; Darwin démontra que celles-ci éloignent les deux corps et égalisent ainsi leurs vitesses de rotation. Après que ces processus ont fonctionné pendant des millions d’années, les vitesses de rotation des deux corps et leur vitesse de révolution l’une autour de l’autre doivent toutes devenir égales, de sorte que chaque corps tourne perpétuellement la même face vers son compagnon, et que les deux tournent l’une autour de l’autre comme les deux masses d’un haltère reliées par un bras invisible.
Bien qu’un soleil et une planète ne forment pas un système binaire au sens strict du terme, ils sont nécessairement soumis aux mêmes forces que les véritables systèmes binaires. Ainsi, nous pouvons observer l’effet du frottement de marée dans le fait que Mercure tourne toujours la même face vers le Soleil, et que Vénus tourne si lentement sur son axe qu’elle lui tourne la même face jour après jour, et probablement aussi semaine après semaine. À mesure que nous progressons dans l’espace, les effets du frottement de marée diminuent rapidement, mais il est probablement significatif que les planètes les plus proches, la Terre et Mars, aient des jours d’environ 24 heures chacune, tandis que les planètes plus éloignées, Jupiter, Saturne et Uranus, n’ont chacune des jours que d’environ 10 heures. Les périodes de rotation de Neptune et de Pluton sont inconnues. En dehors de cela, nous constatons, d’une manière générale, que plus nous nous éloignons du soleil, plus les planètes tournent rapidement, ce qui est précisément l’effet que devrait produire le frottement des marées.
De la même manière, le frottement des marées est probablement le principal responsable de la configuration actuelle du système Terre-Lune, éloignant la Lune de la Terre à sa distance actuelle et la faisant toujours tourner du même côté vers nous. Le frottement des marées doit bien sûr toujours être à l’œuvre. La Lune est responsable de la majeure partie des marées qui se forment dans les océans terrestres ; celles-ci, en exerçant une traction sur la Terre solide située en dessous, ralentissent sa vitesse de rotation, ce qui fait que le jour s’allonge continuellement et continuera ainsi jusqu’à ce que la Terre et la Lune tournent et tournent à l’unisson. Lorsque ce moment arrivera, si jamais ce moment arrive, la Terre tournera continuellement du même côté vers la Lune, de sorte que les habitants de l’un des hémisphères terrestres ne verront jamais la Lune, tandis que l’autre côté sera éclairé par elle chaque nuit. À ce moment-là, la durée du jour et du mois sera identique, chacune équivalant à environ 47 de nos jours actuels. Jeffreys a calculé que cet état de choses pourrait être atteint après environ 50 milliards d’années.
Après cela, le frottement des marées n’opérera plus dans le sens où il éloignerait la Lune de la Terre. L’effet combiné des marées solaires et lunaires sera de ralentir encore davantage la rotation de la Terre, la Lune diminuant en même temps progressivement sa distance à la Terre. Lorsqu’elle aura finalement, après des siècles inimaginables, été entraînée jusqu’à environ 19 000 kilomètres de la Terre, les marées soulevées par la Terre dans le corps solide de la Lune briseront cette dernière en fragments (p. 250 ci-dessous), qui formeront un système de minuscules satellites tournant autour de la Terre de la même manière que les particules des anneaux de Saturne tournent autour de Saturne, ou que les astéroïdes tournent autour du Soleil.
Nous avons déjà remarqué comment la disposition actuelle du système Terre-Lune nous permet de calculer l’âge de la Terre ; Jeffreys estime que le système a dû prendre quelque chose de l’ordre de 4000 millions d’années pour atteindre sa configuration actuelle (p. 155).
Cette période, qui paraît si longue à l’échelle terrestre, n’est qu’un instant dans la vie d’une étoile. Les composantes d’une véritable étoile binaire atteignent une configuration semblable à celle du système Terre-Lune en une brève fraction de leur vie, et, en passant, atteignent avec le temps la configuration où chacune tourne perpétuellement la même face vers l’autre. Jusqu’à présent, le frottement de marée a éloigné les masses de plus en plus, mais dès que ce stade est atteint, les marées deviennent stationnaires sur les deux composantes, de sorte que le frottement de marée cesse d’agir. Ainsi, la séparation produite par le frottement de marée a atteint sa limite, et, en ce qui concerne le frottement de marée, les deux corps pourraient tourner de la manière décrite ci-dessus pour l’éternité.
Perte de poids. À mesure que le frottement des marées devient inopérant, un nouvel agent entre en jeu. Nous avons calculé que le Soleil perd du poids au rythme de [ p. 227 ] 250 millions de tonnes par minute, qu’il perd du poids à ce rythme, ou à un rythme comparable, depuis des millions de millions d’années, et qu’il continuera de le faire pendant des millions de millions d’années encore. La Terre est à sa distance actuelle du Soleil parce que cette distance est exactement adaptée au poids actuel du Soleil. Si le poids du Soleil était soudainement réduit de moitié, son attraction gravitationnelle sur la Terre serait également réduite de moitié, et la Terre s’éloignerait davantage du Soleil[3].
Il est peu probable que le poids du Soleil soit soudainement réduit de moitié, mais il a été réduit d’un milliard de tonnes au cours des quatre dernières minutes, ce qui a affaibli son emprise gravitationnelle sur la Terre et l’a déplacée sur une orbite plus large ; à cet instant, le rayon de l’orbite terrestre est plus grand qu’il y a quatre minutes. Les détails peuvent être retracés mathématiquement avec une précision absolue. Il apparaît que l’orbite terrestre autour du Soleil n’est pas un cercle, ni même une ellipse de faible excentricité ; c’est une courbe en spirale, comme un ressort de montre déroulé. Chaque année, la Terre s’enfonce un peu plus dans le froid et l’obscurité ; un calcul précis montre que sa distance moyenne au Soleil augmente au rythme d’environ un mètre (39,37 pouces) par siècle. L’effet est bien sûr du même type que celui que nous avons vu se produire dans le système galactique par la perte de poids des étoiles. La seule différence est que dans la galaxie, un système de milliers de millions d’étoiles est en expansion, alors que le système Soleil-Terre n’est constitué que de deux membres.
[ p. 228 ] Des effets exactement similaires doivent être produits par la perte de poids des deux composantes d’une étoile binaire. Dans ce cas, les deux composantes rayonnent de l’énergie et perdent donc simultanément du poids. Un calcul détaillé montre qu’elles doivent continuellement s’éloigner l’une de l’autre, mais que la forme de leur orbite ne subira aucun changement.
Ni séparément ni ensemble, les deux effets décrits ci-dessus n’expliquent la forme ni la taille des orbites observées des étoiles binaires dans leur ensemble. Pour les interpréter, nous devons faire appel à un troisième agent : les forces gravitationnelles des étoiles passantes. Nous avons déjà vu comment celles-ci expliquent la distribution statistique des orbites réellement observée.
La combinaison de ces trois facteurs – le frottement des marées, qui s’étend sur des millions d’années, la perte de masse, qui s’étend sur des millions de millions d’années, et les perturbations dues au passage des étoiles, qui s’étendent sur une période similaire – est responsable de l’évolution des systèmes d’étoiles binaires. Leur effet cumulé est d’élargir la distance entre les deux étoiles, tout en déformant leur orbite.
Subdivision. Tandis que ces changements se produisent dans la disposition orbitale d’un système binaire, les deux composants changent eux-mêmes leur condition physique en raison de leur perte continue de poids, et, comme pour les étoiles mères, cette perte de poids se traduit généralement par un rétrécissement de la taille de l’étoile. Le rétrécissement de l’un ou l’autre composant du système fait passer sa forme par la séquence de configurations que nous avons déjà énumérées, et si le rétrécissement se poursuit suffisamment longtemps, le composant peut finir par se diviser en deux masses distinctes. [ p. 229 ] L’un ou les deux constituants d’un système binaire peuvent ainsi se subdiviser en sous-systèmes binaires, donnant naissance à un système de trois ou quatre étoiles. H.N. Russell a démontré mathématiquement que lorsqu’un système binaire P, Q se divise en un système triple, P, q, q’, par la décomposition de Q en deux constituants q, q’, la distance entre q et q’ ne peut dépasser environ un cinquième de la distance initiale PQ. Cette loi théorique est bien confirmée par l’observation. La figure 13 montre un système multiple typique, et nous remarquons que les séparations dans chacun des différents sous-systèmes sont toutes très faibles en comparaison de celles des systèmes principaux.

Le développement du chaos primitif hypothétique a maintenant été retracé à travers cinq générations de corps astronomiques,
chaos — nébuleuses — étoiles — systèmes binaires — sous-systèmes,
à laquelle il faut ajouter une sixième génération si les étoiles du sous-système se divisent davantage, comme c’est le cas, par exemple, dans l’étoile représentée sur la figure 13. La généalogie des étoiles commence par une vaste nébuleuse ténue remplissant tout l’espace ; la dernière génération est constituée de petites étoiles rétrécies et mourantes, incapables de subdivision ultérieure. La généalogie a été établie principalement sur des bases théoriques, mais nous ne devons pas douter de son exactitude générale, car l’observation la confirme à maintes reprises et à presque chaque étape. En fait, il n’est guère exagéré de dire que la séquence évolutive aurait pu être découverte [ p. 230 ] presque aussi bien à partir de simples preuves observationnelles, à l’exception de l’hypothétique chaos primitif, sur lequel, de par la nature des choses, l’observation ne peut rien dire.
¶ L’origine du système solaire
Presque toutes les formations astronomiques observées peuvent être classées dans la séquence évolutive que nous venons d’évoquer, avec une certitude relative ou une plausibilité raisonnable, à l’exception d’une exception remarquable et flagrante : le système solaire. La cosmogonie est née d’une tentative de découverte de l’origine du système solaire. Les raisons pour lesquelles elle a limité ses efforts à ce problème particulier sont chronologiques ; à ses débuts, l’astronomie n’avait guère conscience de l’existence de l’extérieur du système solaire. L’aperçu que nous venons de donner des découvertes de la cosmogonie scientifique moderne est remarquable en ce qu’il montre que la cosmogonie nous fait faire le tour de l’univers, expliquant l’origine et le cycle de vie de pratiquement chaque objet rencontré au cours de ce voyage, puis nous laisse sans voix lorsqu’elle revient à son point de départ et se retrouve confrontée à son berceau, le système solaire.
L’hypothèse nébulaire de Laplace. La première cosmogonie scientifique sérieuse fut celle incarnée par la célèbre hypothèse nébulaire de Laplace. En 1755, Kant avait imaginé un chaos primitif se condensant en nébuleuses en rotation et, identifiant l’une de ces nébuleuses au Soleil, avait imaginé que les planètes se formaient par la solidification de masses de gaz libérées par la nébuleuse, à la manière dont nous avons supposé la naissance des étoiles. En 1796, Laplace avança des idées similaires, qu’il développa en détail avec une précision mathématique [ p. 231 ] bien au-delà des capacités de Kant. Il montra comment, à mesure que son rétrécissement la faisait tourner de plus en plus vite, une masse de gaz en rotation s’aplatissait, développait la forme lenticulaire dont nous avons déjà parlé (fig. 3 de Planche XVI), puis procédait à l’éjection de matière dans son plan équatorial, ou plutôt à son abandon à mesure que le rétrécissement de la masse principale continuait. À ce stade, elle ressemblerait quelque peu aux nébuleuses représentées aux fig. 4 et 5 de Planche XVI, bien que Laplace, ne connaissant pas ce type de nébuleuses, ait cité Saturne entouré de ses anneaux comme exemple de la formation attendue à ce stade ([Planche XXIV](#Universe_plate_14, p. 250). Laplace imaginait que la frange de gaz abandonnée se condenserait alors et formerait une seule planète. À mesure que la masse principale diminuait, davantage de gaz fut abandonné dans le plan équatorial, lequel se condensa en une autre planète, et ainsi de suite, jusqu’à ce que le Soleil cesse de rétrécir et qu’aucune autre planète ne naisse. Une répétition du même processus, mais à une échelle bien plus réduite, aboutit à la naissance des satellites à partir des planètes.
Que l’hypothèse soit a priori plausible est évident du fait qu’elle a survécu, et même été généralement acceptée, pendant près d’un siècle avant de rencontrer une opposition sérieuse. Récemment, des critiques se sont accumulées, d’une importance telle qu’elles ont clairement démontré la nécessité de l’abandonner.
Selon Laplace, le Soleil s’est désintégré et a donné naissance à des planètes par excès de rotation. Pourtant, la théorie et l’observation indiquent clairement le sort réservé à une étoile qui tourne trop vite pour être en sécurité ; elle ne fonde pas de famille, mais éclate simplement, tel un volant d’inertie surmené, en fragments de taille presque égale. Les systèmes binaires et multiples spectroscopiques sont les vestiges d’étoiles qui se sont désintégrées par excès de rotation, et ils ne ressemblent en rien au système solaire.
De nouveau, le principe de « conservation du moment angulaire » exige que la rotation du Soleil primordial persiste dans la rotation du Soleil actuel et dans les révolutions des planètes autour de lui. En additionnant les contributions de toutes ces variables, nous obtenons un total qui devrait représenter le moment angulaire du Soleil primordial. En toute rigueur, une contribution supplémentaire devrait être ajoutée, compte tenu du poids de tout le rayonnement émis par le Soleil depuis la naissance des planètes. Nous pouvons calculer le montant de cette contribution, car nous connaissons l’âge de la Terre avec une précision acceptable, mais elle s’avère totalement négligeable.
Le moment angulaire total du Soleil primitif peut être calculé avec une assez bonne précision, car plus de 95 % du moment angulaire total du système solaire actuel réside dans le mouvement orbital de Jupiter. Cette contribution peut être calculée avec une grande précision, de sorte que l’incertitude relative aux contributions mineures qui constituent les 5 % restants n’a que peu d’influence sur le total.
Lorsque ce total est calculé, un fait surprenant apparaît : le Soleil primitif ne pouvait pas avoir eu une rotation suffisante pour provoquer une quelconque fragmentation. De toute évidence, le Soleil est très loin d’être fragmenté par sa rotation actuelle. L’aplatissement de la figure est la première étape vers la fragmentation, et la figure du Soleil est si peu aplatie par sa rotation actuelle que les mesures les plus précises n’ont jusqu’à présent détecté aucun aplatissement. En ajoutant le moment angulaire supplémentaire représenté maintenant par les mouvements de Jupiter et de tous les autres membres du système solaire, nous obtenons un Soleil primitif tournant [ p. 233 ] à peu près aussi vite que Jupiter tourne actuellement, et présentant à peu près le même degré d’aplatissement de la figure que Jupiter – suffisamment pour être mesuré assez facilement dans un télescope, ou même pour être détecté à l’œil nu, mais pas assez pour provoquer une fragmentation.
Il est peu probable que le Soleil ait beaucoup changé depuis la naissance de ses planètes, car les quelque 2 milliards d’années écoulées ne représentent qu’une infime fraction de sa vie totale. Si, toutefois, nous imaginons qu’il a sensiblement rétréci durant cet intervalle, le moment cinétique disponible aurait été encore plus impuissant à briser le grand Soleil primitif qu’il ne l’est à briser le Soleil rétréci actuel. Quel que soit l’angle sous lequel nous envisageons les choses, nous concluons que le Soleil ne peut s’être brisé, comme l’imaginait Laplace, par excès de rotation ; en effet, il n’a jamais pu posséder plus qu’une infime fraction de la rotation nécessaire à sa fragmentation.
Une troisième objection est d’une nature quelque peu différente. Laplace était un très grand mathématicien, et sa théorie mathématique abstraite était tout à fait correcte, jusqu’à présent. Des analyses modernes plus raffinées l’ont confirmé à chaque étape, et l’observation fait de même, comme en témoignent les photographies de nébuleuses en rotation (Planche XVI). Ces photographies montrent un processus se déroulant sous nos yeux, essentiellement identique à celui imaginé par Laplace, à l’exception d’une différence d’échelle colossale. Tout se passe qualitativement comme Laplace l’imaginait, mais à une échelle incomparablement plus grande que celle dont il avait jamais rêvé. Sur ces photographies, la nébuleuse primitive n’est pas un seul soleil en formation, mais contient suffisamment de matière pour former des centaines de millions de soleils ; les condensations ne forment pas de petites planètes de la taille de notre Terre, mais sont elles-mêmes des soleils ; ils ne sont pas au nombre de huit ou plus, mais il faut les compter en millions.
On peut se demander pourquoi la même chose ne peut se produire à l’échelle plus petite imaginée par Laplace — car les conclusions des mathématiques ne sont-elles pas applicables indépendamment de la taille du corps auquel nous avons affaire ? La réponse a en effet déjà été donnée (p. 218). Tout se déroule à plus petite échelle selon un plan jusqu’à la formation des condensations ; ici, la question d’échelle s’avère vitale. Nous avons vu (p. 196) comment les molécules qui forment le soleil se sont condensées en une étoile en raison de leur grand nombre ; les molécules dans une pièce ne se condensent en rien du tout parce qu’elles sont trop peu nombreuses. De même, les molécules laissées par le lent rétrécissement d’un soleil (en supposant pour l’instant que celui-ci tourne suffisamment vite pour laisser des molécules derrière lui) ne se condenseraient pas, car à tout instant, il y en aurait trop peu disponibles pour la condensation. Elles seraient répandues par gouttes, et une goutte de gaz ne se condense pas mais se disperse dans l’espace. Un calcul mathématique tranche définitivement la question, et cette décision est totalement contraire à l’hypothèse de Laplace. Hormis quelques détails mineurs, le processus imaginé par Laplace explique la naissance des soleils à partir de nébuleuses ; il ne peut expliquer la naissance des planètes à partir de soleils.
Théories du second corps. Laplace imaginait son soleil seul dans l’espace, même ses plus proches voisins étant trop éloignés pour l’influencer de quelque manière que ce soit. C’était une supposition naturelle ; nous avons déjà remarqué combien il est extrêmement rare que deux étoiles se rapprochent suffisamment pour s’influencer mutuellement. Pourtant, aucun mode d’évolution possible d’une étoile restée seule dans l’espace ne semble pouvoir expliquer l’origine du système solaire. Dès 1750, Buffon avait suggéré que le système solaire aurait pu être produit par la perturbation du soleil par un autre corps, qu’il décrivait comme une « comète ». En proposant son hypothèse nébulaire, Laplace a mentionné l’idée de Buffon, mais l’a rejetée assez sèchement au motif qu’elle semblait incapable d’expliquer les orbites presque circulaires des planètes – une objection mal fondée, comme nous le verrons bientôt. Mais lorsque nous constatons qu’une seule étoile ne peut pas donner naissance à elle seule à un système solaire, il devient naturel d’étudier ce qui se passe dans les rares cas où l’évolution d’une étoile est dirigée vers d’autres chemins par l’approche d’une seconde étoile.
En 1880, Bickerton, de Nouvelle-Zélande, reprenant l’idée de Buffon, supposa que le système solaire avait été formé par la collision du Soleil avec une autre étoile. Il imagina que les débris de la collision formaient un troisième corps nébuleux, dont les condensations formaient les planètes. Il montra comment la résistance que les planètes rencontreraient en se déplaçant dans la nébuleuse environnante rendrait progressivement leurs orbites plus circulaires, expliquant ainsi leurs formes actuelles presque circulaires. Dix ans plus tôt, l’écrivain anglais RA Proctor avait avancé des idées similaires, quoique avec moins de précision. En 1905, les professeurs Chamberlin et Moulton de Chicago proposèrent une modification de ces mêmes idées, sous le nom d’« hypothèse planétésimale ». Abandonnant l’idée de collision matérielle, ils supposèrent qu’une étoile passante exerçait une puissante attraction de marée sur le Soleil, ce qui avait pour résultat que les protubérances solaires ordinaires atteignaient temporairement une violence extraordinaire ; La matière éjectée était censée s’élever à des hauteurs inhabituelles et se condenser en petits corps solides, les « planétésimaux », à partir de l’agrégation de [ p. 236 ] lesquels les planètes se sont finalement formées. Ces diverses théories étaient toutes purement spéculatives. Elles ont montré très peu de capacité à survivre à l’épreuve décisive de l’analyse mathématique, ou à expliquer les caractéristiques les plus saillantes du système solaire ; aucune d’entre elles, par exemple, n’explique pourquoi les plus grandes planètes du système solaire sont accompagnées de familles de satellites.
Trois ans avant que Chamberlin et Moulton ne présentent leur théorie des planétésimaux, j’avais spéculé sur la possibilité que des forces de marée fragmentent une étoile et engendrent un système solaire. En 1916, j’ai étudié mathématiquement ce qui se passerait réellement lorsqu’une étoile exerce de violentes forces de marée sur une autre. Les résultats obtenus m’ont semblé réfuter la théorie des planétésimaux de Chamberlin et Moulton, et m’ont conduit à proposer l’actuelle « théorie des marées », qu’une grande partie des astronomes, je crois, admet aujourd’hui comme donnant l’origine la plus probable du système solaire ; elle ne peut évidemment prétendre à la finalité ni à la certitude.
Théorie des marées. Lorsque deux étoiles ou autres corps se croisent sans collision, l’effet principal doit être que chacun d’eux provoque des marées chez l’autre. Plus on se rapproche, plus les marées sont hautes en général, même si la vitesse de croisement des corps doit aussi jouer un rôle, car elle détermine la durée de leur influence mutuelle.
Il est probable que les deux bras spiraux qui donnent leur nom et leur aspect caractéristique aux nébuleuses spirales doivent leur origine à une action de marée assez similaire. Les conditions sont ici différentes : la rotation des nébuleuses les amène de toute façon à émettre de la matière dans leurs plans équatoriaux, de sorte que même de faibles forces de marée devraient alors entraîner la concentration de cette matière [ p. 237 ] en deux bras symétriques. Dans des conditions stellaires, un rapprochement beaucoup plus étroit est nécessaire pour extraire la matière de l’étoile, et il est alors très probable qu’il y aura deux bras inégaux et dissemblables, ou peut-être un seul.
Si l’on s’approche très près, les marées peuvent prendre un aspect totalement différent des faibles marées que le Soleil et la Lune soulèvent dans nos océans ; elles peuvent prendre la forme exagérée de hautes montagnes de matière se déplaçant à la surface de l’étoile. Un rapprochement encore plus rapproché peut transformer ces montagnes en longs bras de gaz extraits du corps de l’étoile. Si, comme c’est généralement le cas, les deux étoiles sont de poids inégaux, la plus petite subira généralement plus de perturbations que la plus lourde.
La naissance des planètes. Le long bras ou filament de matière extrait d’une étoile par l’effet de marée est d’abord continu dans sa structure, mais l’analyse montre qu’il constitue un sujet propice à l’opération de ce que nous avons appelé « l’instabilité gravitationnelle ». Des condensations commencent à se former dans ce long bras de gaz, comme décrit précédemment. Comme précédemment, les plus petites condensations se dissipent, tandis que les plus grandes augmentent d’intensité jusqu’à ce que le filament se brise en plusieurs masses détachées ; des planètes sont nées de la plus petite étoile. Les paires de nébuleuses montrées dans la Planche XXII et la moitié supérieure de la Planche XXIII sont très probablement sous l’influence des marées l’une de l’autre, et peuvent servir à suggérer la nature générale du processus que nous considérons maintenant, bien qu’il faille se rappeler que tout ce qui se passe ici se produit à une échelle énormément plus grande que celle du système solaire — si ce n’était pas le cas, le télescope serait totalement incapable de nous le montrer.
Lorsque les planètes naissantes commencent à se déplacer comme des corps séparés et indépendants, elles sont soumises à l’attraction gravitationnelle des deux étoiles et décrivent ainsi des orbites très complexes. Progressivement, la plus grande étoile s’éloigne jusqu’à ce que son effet gravitationnel devienne négligeable, et les planètes se retrouvent seules à décrire des orbites autour de la plus petite étoile. Si les planètes se déplaçaient dans un champ d’espace vide, ces orbites seraient des ellipses exactes. Mais le grand cataclysme qui vient de se produire a dû laisser derrière lui toutes sortes de débris. Les comètes, les météores et autres corps mineurs qui subsistent encore dans le système solaire en représentent peut-être une petite partie, mais l’essentiel est probablement resté sous forme de poussière ou de gaz, de sorte que les planètes naissantes ont d’abord dû se frayer un chemin dans un milieu offrant une certaine résistance à leurs mouvements. Dans ces circonstances, leurs orbites ne seraient pas des ellipses strictes. On peut prouver qu’une résistance du genre de celle qui vient d’être décrite changerait la forme des orbites, et qu’avec le temps elles deviendraient plus circulaires, devenant finalement absolument circulaires si le milieu durait assez longtemps.
Les débris de gaz et de poussière seraient cependant continuellement emportés par les planètes et disparaîtraient complètement avec le temps, laissant probablement les orbites planétaires à des niveaux proches de cercles absolus. En supposant que tout cela se soit produit dans le système solaire, il ne reste plus grand-chose des débris originels, les derniers vestiges étant probablement représentés par les particules de poussière responsables de la lumière zodiacale. Néanmoins, le milieu résistant semble avoir existé suffisamment longtemps pour que les orbites, tant des planètes que de leurs satellites, soient pour la plupart quasi circulaires.
Les cas exceptionnels sont tout aussi significatifs que les cas de conformité [ p. 239 ]. Des orbites relativement allongées existent encore précisément dans les régions où l’on s’attendrait à ce que le milieu résistant primitif ait été le plus dispersé dans l’espace, à savoir aux confins du système solaire et des divers systèmes de satellites. Pluton, la planète la plus éloignée de toutes, a une orbite plus allongée que toute autre planète. De même, dans les systèmes de Jupiter et de Saturne, les satellites aux orbites les plus allongées sont ceux qui sont les plus éloignés de leurs planètes primaires. De plus, on peut discerner une tendance générale à associer les orbites allongées à de faibles poids, tant pour les planètes que pour leurs satellites. Mercure, dont le poids n’est que vingt-cinquième de celui de la Terre, possède une orbite très allongée, tout comme, dans une moindre mesure, Mars, dont le poids est un neuvième de celui de la Terre. Jeffreys a proposé une explication à ce phénomène. Des planètes massives comme Jupiter et Saturne ont dû accumuler une importante masse de milieu résistant autour d’elles et l’emporter avec elles à travers l’espace sous la forme d’une vaste enveloppe. Leur mouvement serait freiné par l’interaction de l’ensemble de cette vaste enveloppe avec le reste du milieu, et elles atteindraient ainsi des orbites circulaires plus rapidement que les planètes plus légères, qui avaient accumulé des enveloppes de dimensions bien plus petites. Il en va de même, avec les modifications appropriées, pour les systèmes de satellites.
Jeffreys a calculé la vitesse à laquelle les orbites planétaires changeraient de forme sous l’action de ce milieu résistant. Les données du problème sont nécessairement incertaines, et cette incertitude affecte naturellement ses conclusions, mais son étude a apporté une confirmation précieuse à d’autres estimations du temps écoulé depuis la naissance des planètes.
[ p. 240 ] Nous pouvons maintenant porter notre attention sur les changements physiques qui ont dû affecter les différentes planètes pendant tout ce temps. Le long filament de matière extrait du Soleil était probablement plus riche en matière dans ses parties médianes, ces parties ayant été extraites lorsque la deuxième étoile était la plus proche et que son attraction gravitationnelle était la plus forte. Schématiquement au moins, nous pouvons imaginer ce filament comme ayant la forme d’un cigare – épais près du milieu, fin aux extrémités – de sorte que lorsque les condensations commencent à se former, celles près du milieu sont probablement plus riches en matière que celles des extrémités. Ceci explique probablement pourquoi les deux planètes les plus massives, Jupiter et Saturne, occupent les positions médianes dans la séquence des planètes.
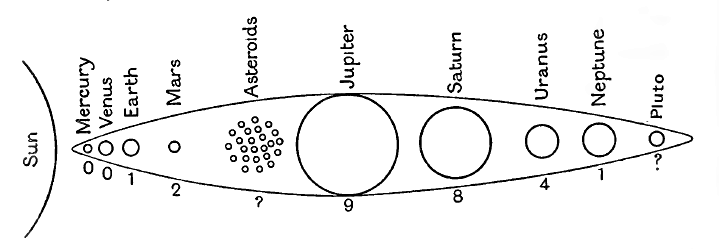
La figure 14 montre les planètes classées selon leur distance au Soleil, leurs tailles étant approximativement à l’échelle. Les milliers d’astéroïdes dont les orbites occupent aujourd’hui l’espace entre celles de Mars et de Jupiter sont représentés comme une seule planète, l’hypothèse générale étant que ces astéroïdes se sont formés par la fragmentation d’un astéroïde initialement plan, d’une manière que nous allons décrire brièvement.
Si nous entourons les planètes d’un contour continu, comme dans le diagramme, nous pouvons reconstituer en imagination [ p. 241 ] le filament en forme de cigare à partir duquel elles ont été produites, et nous voyons immédiatement comment les plus grandes planètes ont été produites là où la matière était la plus abondante.
La théorie des marées, qui prédit toutes ces caractéristiques, a été proposée et ses conséquences ont été déterminées bien des années avant la découverte de la nouvelle planète Pluton. Le fait que Pluton se comporte en tous points conformément aux exigences de la théorie des marées peut donc apporter un précieux soutien à cette théorie.
La naissance des satellites. Nous avons déjà remarqué comment la grande disparité de poids entre le Soleil et les planètes distingue la formation Soleil-planète de celle de l’étoile binaire normale, et suggère ainsi des origines entièrement différentes pour les deux formations. Exactement la même disparité se répète dans les systèmes planète-satellite. Tout comme le soleil parent est énormément plus massif que ses enfants les planètes, de même ces dernières sont à leur tour bien plus massives que leurs enfants satellites. Le Soleil a 1047 fois le poids de sa planète la plus massive et plusieurs millions de fois le poids de la plus petite. Dans le système de Saturne, les chiffres correspondants sont 4150 et environ 16 000 000. La plus proche approche de l’égalité des poids est fournie par le système Terre-Lune, la Terre n’ayant que 81 fois le poids de la Lune. Et, comme le système planétaire du Soleil, les systèmes de satellites de Saturne et, dans une moindre mesure, de Jupiter montrent une tendance générale à ce que les poids des différents satellites augmentent jusqu’à un maximum à mesure que l’on s’éloigne de la planète, puis diminuent à nouveau. Cela suggère à nouveau une formation à partir d’un filament en forme de cigare, la matière étant plus riche près du milieu. Conjointement à la répétition de la grande disparité de poids entre les primaires et les secondaires, cela indique très clairement que les [ p. 242 ] satellites des planètes doivent être nés par le même type de processus qui avait précédemment abouti à la naissance de leurs parents.
On peut imaginer le processus de manière générale. Immédiatement après leur naissance, les planètes doivent commencer à se refroidir. Les plus grosses planètes, Jupiter et Saturne, se refroidissent naturellement plus lentement, tandis que les plus petites le font plus rapidement. Ces dernières peuvent perdre de la chaleur si rapidement qu’elles se liquéfient, voire se solidifient, presque immédiatement après leur naissance. Pendant que ces événements se produisent, les planètes poursuivent des orbites quelque peu erratiques, décrivant lesquelles elles peuvent passer si près du Soleil qu’une seconde série de perturbations par les marées se produit. Dans ces cas, le Soleil lui-même joue le rôle initialement joué par l’étoile de passage venue de l’espace, les planètes jouant celui du Soleil. Le Soleil peut alors arracher de longs filaments de matière à la surface des planètes, et ceux-ci, formant des condensations, peuvent donner naissance à une nouvelle génération de corps célestes, les satellites des planètes. C’est ainsi que la théorie des marées imagine que les satellites planétaires ont vu le jour.
Des recherches mathématiques montrent que plus une planète était liquide à sa naissance, moins elle risquait d’être fragmentée par le Soleil encore gazeux. Si, toutefois, une telle fragmentation se produisait, les poids des planètes primaires et satellites seraient plus proches de l’égalité que si la planète avait été plus gazeuse. Ainsi, en passant de planètes entièrement gazeuses à des planètes liquéfiées à leur naissance ou immédiatement après, on devrait s’attendre d’abord à trouver des planètes dotées d’un grand nombre de satellites relativement petits, puis, après avoir franchi les cas limites des planètes dotées d’un petit nombre de satellites relativement grands, à trouver des planètes dépourvues de satellites.
[ p. 243 ] Nous avons déjà vu que les grandes planètes centrales, Jupiter et Saturne, auraient dû rester gazeuses plus longtemps et les plus petites planètes se liquéfier plus tôt ; nous voyons maintenant que cette prédiction de la théorie décrit exactement ce que l’on trouve réellement dans le système solaire. En partant de Jupiter et Saturne, chacun avec neuf satellites relativement petits, nous passons devant Mars avec seulement deux satellites, et arrivons à la Terre avec son seul satellite relativement grand, suivi de Vénus et Mercure qui n’ont aucun satellite du tout. En continuant dans l’autre sens, nous quittons Jupiter et Saturne avec chacun leurs neuf minuscules satellites, pour découvrir Uranus avec quatre petits satellites et Neptune avec un satellite relativement grand. Le nombre placé sous chaque planète dans la fig. 14 donne le nombre de ses satellites. Lorsque les nombres sont présentés de cette manière, l’ordre dans la disposition des systèmes de satellites devient évident, et cette disposition s’avère parfaitement conforme aux prédictions de la théorie des marées. Cette disposition en forme de cigare s’applique non seulement à la taille des planètes, mais aussi, comme il se doit, au nombre de leurs satellites.
La Terre et Neptune, avec un seul satellite chacun, et ceux qui sont relativement grands, forment les lignes de démarcation évidentes entre les planètes initialement liquides et celles initialement gazeuses. Ceci nous amène à supposer que Mercure, Vénus et Pluton ont dû devenir liquides ou solides immédiatement après leur naissance, que la Terre et Neptune étaient en partie liquides et en partie gazeuses, et que Mars, Jupiter, Saturne et Uranus sont nés gazeux et sont restés gazeux au moins jusqu’à la naissance de leurs familles de satellites.
Nous pourrions peut-être trouver d’autres preuves confirmant [ p. 244 ] la théorie des marées dans le cas où les poids de Mars et d’Uranus sont anormalement faibles compte tenu de leur position dans la séquence planétaire. Si, comme nous l’avons supposé, les planètes étaient toutes nées d’un filament continu de matière, le poids de Mars à la naissance aurait très probablement été intermédiaire entre ceux de la Terre et de Jupiter, et celui d’Uranus intermédiaire entre ceux de Neptune et de Saturne. Mais si, comme nous l’avons déjà supposé, les deux planètes anormales Mars et Uranus étaient les deux plus petites planètes à être nées à l’état gazeux, elles perdraient probablement davantage de leur substance que les autres planètes, leurs couches moléculaires les plus externes se dissipant dans l’espace avant d’avoir refroidi à l’état liquide. Si Mars et Uranus sont censés être de simples reliques de planètes initialement bien plus massives qu’elles ne le sont aujourd’hui, les anomalies commencent à disparaître et les pièces du puzzle à s’assembler de manière très satisfaisante.
Plans orbitaux. Toute masse en rotation, qu’elle soit gazeuse, liquide ou solide, possède un axe de rotation défini et, perpendiculairement à celui-ci, un plan équatorial défini qui la divise symétriquement en deux moitiés exactement égales et semblables. Lorsqu’une masse se brise sous l’effet de sa propre rotation, le plan équatorial et la symétrie persistent. On en trouve des illustrations dans n’importe quelle série de photographies de nébuleuses en rotation, comme celles des planches XV et XVI. Dans la vie plus humble, une illustration est fournie par les éclaboussures de boue projetées par une roue de bicyclette en rotation, qui restent toutes dans le plan dans lequel la roue tourne.
Si le plan équatorial du Soleil s’était avéré être un plan de symétrie du système solaire, de sorte que l’ensemble du système était disposé de manière similaire des deux côtés de ce plan, il aurait peut-être été possible d’expliquer le système comme le résultat d’une rupture rotationnelle. Mais le plan équatorial du Soleil n’est pas un plan de symétrie. Les planètes ne s’y déplacent pas, la plupart d’entre elles se déplaçant dans un plan qui forme avec lui un angle de 5 ou 6 degrés. Pour reprendre notre humble analogie, les éclaboussures de boue ne volent pas dans le plan où tourne la roue de bicyclette.
L’hypothèse selon laquelle les planètes seraient nées d’une rupture rotationnelle du Soleil s’effondre complètement devant ce fait, mais la théorie des marées en fournit d’emblée une explication simple. Le Soleil tourne toujours, comme avant la naissance des planètes, et conserve donc son plan équatorial originel. Le plan, très différent, ou très proche, dans lequel les planètes décrivent leurs orbites doit clairement être celui dans lequel le long filament de marée a été initialement étiré par l’étoile qui passe. Ainsi, le plan dans lequel évoluent actuellement les planètes extérieures doit enregistrer la position du plan dans lequel les deux étoiles, le Soleil et l’étoile errante, deuxième parent de la famille des enfants du Soleil, ont décrit des orbites l’une autour de l’autre il y a 2 milliards d’années. C’est le seul indice que ce dernier ait conservé de son identité, et il est bien sûr bien trop faible pour permettre une identification après ce long laps de temps.
En résumé, nous avons vu que le mécanisme normal par lequel la plus grande partie de l’univers a été sculptée est la naissance de générations successives de corps astronomiques par l’action de « l’instabilité gravitationnelle ».
La généalogie normale se déroule à peu près comme suit :
_chaos — nébuleuses — étoiles — systèmes binaires — sous-systèmes. _
[ p. 246 ] Toutes les étoiles ne sont pas passées au-delà des deux dernières générations ; là où seule une faible rotation était présente, une étoile pourrait bien vivre toute sa vie sans subdivision supplémentaire. Notre Soleil en aurait fourni un exemple s’il n’y avait pas eu le rare accident du rapprochement d’une seconde étoile. De l’interaction de ces deux étoiles, deux autres générations ont vu le jour, toujours par le mécanisme de l’instabilité gravitationnelle. Pour notre système solaire, comme pour tout autre système similaire existant dans le ciel, la généalogie est la suivante :
chaos — nébuleuse — soleil — planètes — satellites.
Les deux types de généalogie présentent cinq générations, chacune issue de son parent sous l’effet de l’instabilité gravitationnelle. À elles deux, ces généalogies incluent la quasi-totalité des objets astronomiques de grande taille que nous connaissons. Il est donc juste de dire que l’« instabilité gravitationnelle » semble être le principal facteur responsable de l’architecture fondamentale de l’univers.
Limite de Roche. Le règne de l’instabilité gravitationnelle doit prendre fin avec la naissance des satellites planétaires, car les corps gazeux de moindre masse ne pourraient se maintenir ensemble. Même dans les circonstances les plus favorables, leur faible attraction gravitationnelle serait incapable d’empêcher leurs molécules les plus externes de s’échapper, de sorte que toute la masse se disperserait rapidement dans l’espace. Pourtant, l’astronomie fournit de nombreux exemples de corps plus petits ; nous avons déjà mentionné les astéroïdes, les météores ou étoiles filantes, et les particules des anneaux de Saturne. Comme tous ces corps sont trop petits pour être nés à l’état gazeux, nous devons supposer qu’ils sont les fragments fragmentés de masses plus grandes. Cela concorde avec le fait que ces petits corps [ p. 247 ] n’apparaissent généralement pas individuellement, mais en essaims.
Les astéroïdes se présentent sous la forme d’un essaim unique. Si on les trouvait dispersés dans tout le système solaire, leur origine pourrait poser un problème complexe. En l’état actuel des choses, l’essaim entier peut être expliqué très simplement par les fragments brisés d’une planète primitive. Les anneaux de Saturne peuvent également être expliqués naturellement par les fragments d’une ancienne lune de Saturne. Les comètes, que nous avons à peine eu l’occasion de mentionner jusqu’à présent, sont très probablement des essaims de minuscules corps, maintenus ensemble par leur attraction gravitationnelle mutuelle juste assez pour décrire une orbite commune dans l’espace. Lors de son apparition en 1909, on estimait que la comète de Halley réfléchissait autant de lumière solaire qu’un corps unique de 40 kilomètres de diamètre. Pourtant, sa surface apparente était 300 000 fois celle d’un tel corps et était parfaitement transparente. Il est difficile de ne pas conclure que la comète était constituée d’un essaim largement espacé de petits corps, et un tel essaim peut également être expliqué simplement par les fragments brisés d’une masse unique.
Les étoiles filantes, ou météores, se rencontrent également en essaims. Comme nous le verrons plus loin, le mouvement de nombre de ces essaims permet de les identifier comme des comètes fragmentées. Ainsi, les fragments qui composent une comète sont identiques aux météores que nous voyons comme des étoiles filantes lorsqu’ils pénètrent dans l’atmosphère terrestre. Shapley a estimé que l’atmosphère terrestre doit capter des milliards d’étoiles filantes chaque jour, dont une sur cent au maximum est suffisamment brillante pour être visible à l’œil nu. Généralement, elles se dissolvent en vapeur avant d’atteindre la surface terrestre (voir p. 176) ; occasionnellement, une [ p. 248 ] est si grand que l’atmosphère terrestre ne parvient pas à le dissiper entièrement, et ce qui en reste frappe la Terre sous la forme d’un corps solide : une météorite. Chaque étoile filante et météorite peut être considérée comme une comète miniature, constituée d’un seul fragment. Il arrive qu’un groupe entier de fragments, se déplaçant parallèlement à de faibles distances les uns des autres, heurte l’atmosphère terrestre et apparaisse comme une « boule de feu ». En général, tous les petits poissons du système solaire se déplacent en essaims et peuvent naturellement être interprétés comme les fragments fragmentés de corps plus grands.
Si les météorites sont des fragments de corps célestes nés du Soleil en même temps que les planètes, elles ont dû se solidifier à peu près au même moment que la Terre, à une époque que nous avons située il y a environ 2 milliards d’années. Mais si elles étaient nées d’une autre étoile, leur solidification aurait pu remonter à des millions de millions d’années.
Le professeur Paneth et deux collègues de Königsberg ont récemment estimé l’âge de plusieurs météorites par des méthodes similaires à celles employées pour déterminer l’âge de la Terre (p. 154). Ils obtiennent des âges allant de quelques millions d’années à 2 900 millions d’années, mais rien au-delà de ce dernier chiffre. Pas une seule pierre ne suggère un âge approchant même les millions de millions d’années. Cela constitue une preuve irréfutable que ces pierres sont le produit du même cataclysme que celui qui a engendré la Terre, et apporte incidemment une confirmation précieuse de notre précédente estimation de l’âge de la Terre.
On peut facilement imaginer comment des corps plus grands pourraient être fragmentés en essaims de météores. Nous avons supposé que le Soleil avait été fragmenté, au moins au point d’éjecter [ p. 249 ] une famille de planètes, par l’attraction de marée d’une étoile passante. Que se serait-il passé si l’étoile passante n’était pas passée, mais était restée ? Tant qu’elle restait à une certaine distance du Soleil, ses forces de marée tiraient le Soleil en morceaux. On peut imaginer qu’une visite plus longue de sa part aurait entraîné un bouleversement plus important du Soleil et la naissance d’une famille de planètes plus importante. Finalement, une visite d’une durée illimitée aurait brisé le Soleil en fragments.
En 1850, Roche a mené une étude mathématique de ce processus de rupture par marée. Son analyse ne portait que sur les corps solides ou liquides, mais le mécanisme sous-jacent est le même, qu’ils soient solides, liquides ou gazeux. Nous avons vu que le plus petit des deux corps impliqués dans une rencontre de marée est celui qui souffre le plus. Roche n’a traité que le cas où un corps était très petit par rapport à l’autre ; dans ce cas, le petit corps était complètement brisé, tandis que le plus grand restait indemne. Roche a imaginé que le petit corps décrivait une orbite de taille progressivement décroissante autour du grand corps. Si les deux corps étaient de densité égale, il a calculé que le petit corps se briserait dès que le rayon de son orbite tomberait à 2,45 fois le rayon du grand corps. Si les corps sont de densité différente, la question est légèrement plus compliquée. Il faut imaginer que le plus grand corps se dilate ou se contracte jusqu’à atteindre la même densité moyenne que le plus petit ; la distance critique est alors de 2,45 rayons du plus grand corps dans son état imaginaire de dilatation ou de contraction.
Cette distance est généralement connue sous le nom de limite de Roche. Un satellite peut décrire en toute sécurité une orbite circulaire autour de son astre principal tant que cette orbite se situe au-delà de la limite de Roche, mais elle se fragmente dès qu’il franchit cette limite. Les chiffres suivants confirment l’analyse mathématique de Roche :
| Rayon | Valeur |
|---|---|
| Rayon de l’anneau extérieur de Saturne | 2,30 rayons de Saturne |
| Limite de Roche | 2,45 rayons du primaire |
| Rayon de l’orbite du satellite le plus proche de Saturne | 3,11 rayons de Saturne |
| Rayon de l’orbite du satellite le plus proche de Jupiter | 2,54 rayons de Jupiter |
| Rayon de l’orbite du satellite le plus proche de Mars | 2,79 rayons de Mars |
En même temps, ils suggèrent avec force que les anneaux de Saturne sont les fragments brisés d’un ancien satellite qui s’est aventuré dans la zone dangereuse délimitée par la limite de Roche. Nous avons vu comment notre propre lune est vouée à rétrécir son orbite, jusqu’à être finalement attirée dans la limite de Roche entourant la Terre et brisée en fragments. Après cela, la Terre n’aura plus de lune, mais sera entourée d’anneaux comme Saturne.
On parle des anneaux de Saturne au pluriel, car deux espaces circulaires distincts donnent l’impression de trois anneaux détachés. On a tendance à conclure hâtivement que les anneaux sont les restes brisés de trois satellites distincts, mais ce n’est pas le cas. Goldsbrough a montré comment certaines orbites autour de Saturne sont rendues instables par les mouvements de ses plus gros satellites, de sorte qu’aucune particule ne pourrait y rester en permanence. Il a calculé les positions de ces orbites instables, et celles-ci concordent parfaitement avec les positions des divisions observées entre les anneaux. Ainsi, les anneaux de Saturne ont probablement été produits par la rupture d’un seul satellite. L’anneau de petits satellites que notre lune formera finalement autour de la Terre ne contiendra aucune division, car la Terre n’a pas d’autres lunes susceptibles de rendre certaines orbites instables.

[ p. 251 ] L’idée fondamentale de Roche peut être étendue dans de nombreuses directions et admet des applications variées. Il doit, par exemple, y avoir une zone dangereuse, délimitée par une limite de Roche, entourant le Soleil. La distance de cette zone dangereuse au Soleil dépend de la densité du corps pour lequel elle est dangereuse (p. 249). Pour un corps ayant la faible densité d’une comète, la distance sera en effet très grande. Quelles que soient les distances de leurs zones dangereuses, les comètes doivent occasionnellement les traverser et se briser ce faisant. Deux comètes, la comète de Biela (1846) et la comète de Taylor (1916), ont été observées se briser en deux alors qu’elles se trouvaient à peu près à la distance de la Terre par rapport au Soleil, et en 1882, une comète a été vue se diviser en quatre parties. La comète de Biela est revenue en temps voulu (1852) sous la forme de deux comètes distinctes, distantes de 1 600 000 kilomètres. Depuis, aucune partie de la comète originale n’a été revue. L’orbite de cette comète était identique à celle des météores d’Andromédide, qui forment un spectacle d’étoiles filantes dans l’atmosphère terrestre le 27 novembre, par temps favorable. Il est donc probable que ces étoiles filantes soient les restes brisés de la comète de Biela. D’autres essaims remarquables d’étoiles filantes se déplacent également sur la trajectoire des comètes : les Léonides, qui offraient autrefois un spectacle magnifique tous les 33 ans, se déplacent sur la trajectoire de la comète 1866 I, les Perséides sur celle d’une autre comète (1862 II), et les Aquarides sur celle de la célèbre comète de Halley. Dans chaque cas, il ne fait aucun doute que les étoiles filantes sont des fragments épars des comètes. Il existe en outre plusieurs familles de comètes dont les membres se succèdent en rond sur la même orbite, comme s’ils formaient à l’origine une seule masse.
De la même manière, une limite de Roche doit entourer la planète Jupiter, afin que les comètes et autres corps puissent être brisés en pénétrant dans la zone dangereuse délimitée par cette limite. Le satellite le plus proche de Jupiter s’en trouve déjà dangereusement proche. Mais le plus grand intérêt de cette zone dangereuse particulière est qu’elle explique probablement l’existence des astéroïdes. Aux premiers temps du système solaire, lorsque les orbites des planètes étaient moins circulaires qu’elles ne le sont aujourd’hui, une planète primitive située entre Mars et Jupiter pourrait bien avoir décrit une orbite si allongée qu’elle l’a conduite à plusieurs reprises dans la zone dangereuse de Jupiter. Si tel est le cas, nous n’avons pas besoin de chercher plus loin l’origine des astéroïdes. Il est significatif que l’orbite moyenne de tous les astéroïdes concorde presque exactement avec celle de la planète dont la loi de Bode (p. 19) exigerait qu’elle existe entre Mars et Jupiter.
¶ Notes de bas de page
C’est assez proche, mais pas absolument exact. Une analyse mathématique précise montre que le poids de la condensation minimale M est donné par
où C, γ, ρ, κ sont la vitesse moléculaire, la constante de gravitation, la densité initiale et le rapport des chaleurs spécifiques, tandis que le poids auquel les molécules se déplaçant à la vitesse C ne parviennent pas à s’échapper est donné par
Avec $ \kappa = 1 \frac{2}{3}$ le poids minimum de condensation est de 9,7 fois le poids qui est juste suffisant pour retenir les molécules. ↩︎
Les estimations suivantes ont déjà été mentionnées :
Poids de la galaxie par rapport au soleil : 240 000 000 000
« Nébuleuse M 31 en termes de soleil : 3 500 000 000
„ „ NGC 4594 en termes de soleil : 2 000 000 000 ↩︎Bien que les détails ne soient pas importants, le cours réel des événements serait que la Terre commencerait à décrire une orbite elliptique au lieu d’une orbite circulaire autour du Soleil, la distance moyenne de la Terre étant plus grande qu’aujourd’hui. ↩︎