Auteur : Sir James Jeans, MA, D. Sc., Sc. D., LL. D., FRS
[ p. 253 ] Le processus de formation de l’univers que nous avons examiné dans le dernier chapitre se termine normalement par une étoile simple, bien que des accidents particuliers puissent avoir d’autres conséquences. À la suite de rapprochements rapprochés avec d’autres étoiles, une infime fraction du nombre total d’étoiles, peut-être environ une étoile sur 100 000 (p. 341 ci-dessous), peut être accompagnée d’un cortège de planètes. Une autre fraction, encore petite, bien que bien plus grande que la précédente, semble s’être brisée à la suite d’une rotation excessive et avoir formé des systèmes binaires ou peut-être multiples. Mais le destin de la majorité des étoiles est de poursuivre leur chemin solitaire à travers l’espace, sans se briser d’elles-mêmes ni être brisées par d’autres étoiles. Le seul contact de ces étoiles avec l’univers extérieur réside dans le fait qu’elles déversent sans cesse des radiations dans l’espace. Ce déversement de radiations est presque entièrement à sens unique : le rayonnement qu’une étoile peut recevoir d’autres étoiles est insignifiant comparé à la quantité qu’elle émet elle-même. Ce rayonnement s’accompagne d’une perte de poids, et là encore, il s’agit d’un compromis : le poids de toute matière dispersée que l’étoile peut emporter de l’espace, comme celui de tout rayonnement qu’elle reçoit, est insignifiant comparé au poids qu’elle perd par rayonnement. Sans vouloir exagérer, l’objet céleste normal peut être idéalisé comme un corps solitaire, seul dans un espace infini, qui déverse continuellement des radiations sans rien recevoir en retour.
Dans ce chapitre, nous examinerons la séquence [ p. 254 ] de changements qu’une telle étoile est susceptible de subir au cours de sa vie. Après avoir déjà évoqué les accidents mécaniques auxquels les étoiles sont exposées, à savoir la fission par rotation et la fragmentation par l’effet de marée d’une étoile passante, nous nous intéressons maintenant à la vie d’une étoile normale qui échappe à tous les accidents jusqu’à son extinction définitive par simple vieillissement.
Il sera nécessaire en premier lieu de décrire les états physiques des différents types d’étoiles observées dans le ciel, et comme préliminaire à cela nous devons expliquer comment les observations de l’astronome sont traduites sous une forme qui nous donne des informations directes sur l’état de l’étoile.
Température de surface. Au chapitre II (p. 140), nous avons vu comment chaque couleur de lumière ou longueur d’onde de rayonnement est associée à une température spécifique, la lumière de cette couleur prédominant lorsqu’un corps est chauffé à cette température. Par exemple, un corps porté à ce que nous appelons une chaleur rouge émet plus de lumière rouge que toute autre couleur, et apparaît donc rouge à l’œil nu.
Ainsi, si une étoile paraît rouge, on peut légitimement en déduire que sa surface est à la température que nous appelons une chaleur rouge. Si une autre étoile a la couleur du carbone d’un arc électrique, on peut conclure que sa surface est à peu près à la même température que l’arc. De cette façon, nous pouvons estimer les températures de surface des étoiles.
En pratique, la procédure n’est pas aussi grossière que la description précédente pourrait le laisser entendre. L’astronome fait passer la lumière d’une étoile à travers un spectroscope, l’analysant ainsi en ses différentes couleurs. Par un processus de mesure précis, il détermine ensuite les proportions dans lesquelles les différentes couleurs de lumière apparaissent. Cela montre immédiatement quelle couleur de lumière est la plus abondante dans le spectre de l’étoile. À partir de cette observation ou de la distribution générale des couleurs, il peut déduire la température de la surface de l’étoile.
Nous avons déjà vu (p. 123) comment Planck a découvert la loi selon laquelle le rayonnement émis par un radiateur plein est distribué entre les différentes couleurs ou longueurs d’onde du spectre. Les quatre courbes montrées dans la fig. 15 représentent la distribution théorique du rayonnement émis par des surfaces aux quatre températures de 3000, 4000, 5000 et 6000 degrés respectivement. Les différentes longueurs d’onde de la lumière sont représentées par des points sur l’axe horizontal, [ p. 256 ] les longueurs d’onde marquées étant mesurées dans l’unité d’un centimillionième de centimètre, que l’on appelle généralement un angström. La hauteur de la courbe au-dessus d’un tel point représente l’abondance du rayonnement de la longueur d’onde en question.
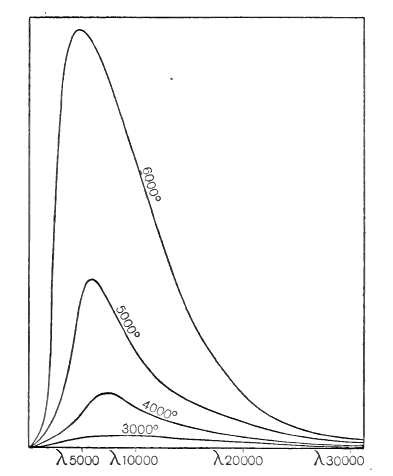
Les deux méthodes de détermination de la température stellaire seront facilement comprises à l’aide de ces courbes. La courbe à 6 000 degrés atteint son maximum à une longueur d’onde de 4 800 Å. Ainsi, si la lumière de longueur d’onde de 4 800 Å est la plus abondante dans le spectre d’une étoile, nous savons que sa surface a une température de 6 000 degrés. La seconde méthode consiste simplement à examiner à laquelle des courbes théoriques présentées à la figure 15 la courbe observée s’ajuste le mieux.
Chacune de ces méthodes indique que la température de la surface du Soleil est d’environ 6 000 degrés absolus, soit près du double de la température de la partie la plus chaude de l’arc électrique. La quantité totale de lumière et de chaleur reçue sur Terre par le Soleil montre que le rayonnement solaire doit être très proche, mais pas tout à fait, du « rayonnement à température maximale » (p. 123) d’un corps à cette température. Ceci est également démontré par la répartition du rayonnement solaire entre les différentes couleurs d’une manière très conforme à la courbe théorique pour un radiateur complet à 6 000 degrés, illustrée à la figure 15.
La température de surface d’une étoile peut également être estimée à partir de son type spectral. De nombreuses raies du spectre stellaire sont émises par des atomes dont un ou plusieurs électrons ont été arrachés par la chaleur de l’atmosphère de l’étoile. Nous connaissons les températures auxquelles les électrons en question sont initialement arrachés à leurs atomes, ce qui permet d’en déduire la température de l’étoile.
[ p. 257 ] Les températures qui correspondent aux différents types de spectres stellaires tels que présentés dans la Planche VIII (p. 51), sont approximativement les suivantes :
| Type spectral | Température |
|---|---|
| B | 23 000 |
| A | 11 000 |
| F | 7 400 |
| G | 6 000 |
| K | 5 100 |
| M | 3 400 |
Les trois dernières entrées du tableau ne concernent que les étoiles normales dont le diamètre est comparable à celui du Soleil. Nous découvrirons (p. 276) qu’il existe une seconde classe d’étoiles (géantes), dont le diamètre est considérablement supérieur à celui du Soleil. Leurs températures sont nettement plus basses, comme indiqué ci-dessous :
| Type spectral | Température |
|---|---|
| G | 5600 |
| K | 4200 |
| M | 3200 |
En étudiant la structure et le mécanisme stellaire, nous nous intéressons moins à la chaleur de la surface de l’étoile, mesurée par sa température, qu’à la quantité de rayonnement qu’elle émet par pouce carré.
Cela dépend bien sûr de la température ; plus une surface est chaude, plus elle émet de rayonnement. Mais la température ne mesure pas la quantité de rayonnement émis. Si nous doublons la température d’une surface, elle émet 16 fois, et non le double, sa quantité précédente de rayonnement ; le rayonnement de chaque pouce carré de surface varie comme la quatrième puissance de la température. [ p. 258 ] Par conséquent, une étoile dont la température de surface est de 3 000 degrés, soit la moitié de celle du Soleil, n’émet qu’un seizième de la quantité de rayonnement par pouce carré que le Soleil[1]. Le rayonnement de chaque étoile est un composé de lumière, de chaleur et de rayonnement ultraviolet, et les proportions de ces éléments ne sont pas les mêmes d’une étoile à l’autre ; plus la surface d’une étoile est froide, plus la fraction de son rayonnement émise sous forme de chaleur est importante. Ainsi, l’étoile à 3 000 degrés n’émettra pas plus d’un seizième de la lumière du soleil par pouce carré, mais émettra plus d’un seizième de la chaleur du soleil.
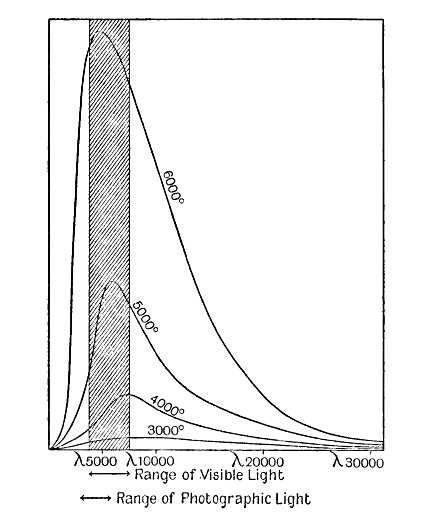
Cela montre que l’émission totale de rayonnement d’une étoile ne peut être estimée à partir de sa seule luminosité visuelle ; une marge substantielle doit toujours être prise en compte pour les rayonnements invisibles, à la fois pour la chaleur invisible à l’extrémité rouge du spectre et pour le rayonnement ultraviolet invisible à l’autre extrémité. L’importance de ces corrections est illustrée dans la fig. 16. Les quatre courbes épaisses sont identiques à celles déjà données dans la fig. 15, et montrent comment le rayonnement d’une étoile de température de surface donnée est distribué sur les différentes longueurs d’onde. Le rayonnement total émis à une température donnée est bien sûr représenté par toute la zone comprise entre la courbe correspondante et l’axe horizontal. L’œil n’est sensible qu’au rayonnement de longueurs d’onde comprises entre 3 750 et 7 500 Å, de sorte que de tout ce rayonnement, seule la partie dans la bande ombrée est visible, tout le reste représentant un rayonnement invisible.
On constate immédiatement qu’une bonne partie du rayonnement émis par une étoile à 6 000 degrés est visible, mais seulement une petite fraction de celui émis par une étoile à 3 000 degrés. Si l’on considère l’ensemble des étoiles [ p. 259 ], la lumière des étoiles ne représente qu’une petite partie de leur rayonnement total.
Si nos yeux devenaient soudainement sensibles à toutes sortes de rayonnements, et pas seulement à la lumière visible, l’apparence du ciel subirait une étrange métamorphose. Les étoiles rouges Bételgeux et Antarès, qui ne sont actuellement que 12e et 16e par ordre de luminosité, brilleraient comme les deux étoiles les plus brillantes du ciel, tandis que Sirius, actuellement la plus brillante de toutes, tomberait à la troisième place. Une étoile de la constellation très peu distinguée d’Hercule serait considérée comme la sixième étoile la plus brillante du ciel. Il s’agit de l’étoile α Herculis, actuellement surpassée par environ 250 étoiles. En raison de sa température extrêmement basse de 2 650 degrés, cette étoile [ p. 160 ] émet son rayonnement presque entièrement sous forme de chaleur invisible. Par exemple, elle émet 60 fois plus de chaleur que l’étoile bleue η Aurigae, dont la température est d’environ 20 000 degrés, mais qui ne reçoit que quatre cinquièmes de cette lumière.
Des marges pour les radiations invisibles ont été prises en compte dans tous les calculs mentionnés dans le présent livre, bien qu’il n’ait pas été jugé nécessaire de les répéter continuellement.
Diamètres stellaires. Il est facile de mesurer le diamètre d’une planète, car celui-ci apparaît au télescope comme un disque de taille finie. Mais les étoiles sont trop lointaines pour que leur diamètre puisse être mesuré de la même manière. Aucune étoile n’apparaît plus grosse dans le ciel qu’une tête d’épingle tenue à une distance de dix kilomètres, et aucun télescope construit à ce jour ne peut représenter un objet de cette taille comme un disque. Toutes les étoiles, même les plus proches et les plus grandes, apparaissent comme de simples points lumineux[2], de sorte que leur diamètre ne peut être mesuré que par des méthodes détournées.
Connaissant la distance d’une étoile, nous pouvons déduire sa luminosité de son éclat apparent. De là, après prise en compte du rayonnement invisible, nous pouvons déduire l’énergie totale libérée par l’étoile : des millions de millions de millions de chevaux-vapeur. Nous connaissons également son énergie libérée par pouce carré de surface, car elle ne dépend que de sa température de surface, déduite directement de l’observation spectroscopique. Connaissant ces deux données, une simple division permet de calculer le nombre de pouces carrés qui composent la surface de l’étoile, ce qui nous indique immédiatement son diamètre.
Les diamètres des étoiles exceptionnellement grandes peuvent être mesurés plus directement par un instrument appelé interféromètre. Lorsque nous braquons un télescope sur une étoile, nous ne voyons pas, à proprement parler, seulement un point lumineux, mais un point lumineux entouré d’un système assez élaboré d’anneaux alternant lumière et obscurité, appelé diagramme de diffraction. On pourrait penser que la taille de ces anneaux nous renseigne sur la taille de l’étoile, mais les deux n’ont rien à voir l’un avec l’autre. Les anneaux représentent un simple défaut instrumental, leur taille dépendant uniquement de la taille et de la disposition optique du télescope. Suivant une méthode suggérée par Fizeau en 1868, le professeur Michelson a montré comment même ce défaut peut être exploité à des fins utiles et, grâce à elle, a produit ce qui est peut-être l’instrument le plus ingénieux et le plus sensationnel au service de l’astronomie moderne : l’interféromètre. En effet, cet instrument superpose deux diagrammes de diffraction distincts de la même étoile et les compare l’un à l’autre de manière à révéler la taille de l’étoile qui les produit. Les diamètres de quelques-unes des plus grandes étoiles ont été mesurés de cette manière, de sorte que nous pouvons dire que nous connaissons leurs tailles par observation directe. Dans tous les cas, le diamètre mesuré directement concorde assez bien, quoique pas parfaitement, avec celui calculé indirectement de la manière déjà expliquée. Les écarts, qui ne sont pas graves, semblent provenir du fait que les étoiles rouges ne sont pas de véritables « radiateurs complets » au sens expliqué à la p. 123.
La méthode de l’interféromètre n’est disponible que pour les plus grandes étoiles, mais à l’autre extrémité de l’échelle, la théorie de la relativité est venue à la rescousse. Einstein a démontré qu’une conséquence nécessaire de sa théorie de la relativité est que le spectre d’une étoile devrait être décalé vers le rouge d’une quantité [ p. 262 ] dépendant à la fois du poids et du diamètre de l’étoile. Si, alors, le poids d’une étoile est connu, le décalage spectral observé devrait nous indiquer immédiatement son diamètre. Ce décalage spectral a été récemment observé dans la lumière reçue du compagnon de Sirius, et les mesures de son ampleur conduisent à une valeur pour le diamètre de l’étoile qui concorde exactement avec celle calculée à partir de sa luminosité. Ainsi, aux deux extrémités de l’échelle, pour les étoiles les plus grandes comme pour les plus petites, l’observation directe confirme les valeurs calculées pour les diamètres des étoiles.
Nous pouvons donc avoir pleinement confiance dans les diamètres calculés de toutes les étoiles, même lorsqu’ils ne peuvent être vérifiés par mesure directe. En effet, une divergence entre les diamètres réels et calculés ne peut se produire que d’une seule manière. Les diamètres sont calculés en supposant que les étoiles émettent la totalité de leur rayonnement thermique. Si les étoiles avaient été partiellement transparentes comme les nébuleuses, ou des corps solides comme la Lune, cette hypothèse aurait été fausse, et sa fausseté aurait été immédiatement démontrée par les discordances entre les diamètres calculés et mesurés des étoiles. L’absence de discordances importantes suggère que les étoiles émettent un rayonnement thermique presque complet sur toute la gamme de tailles, de la plus grande à la plus petite.
¶ La variété des étoiles
L’observation montre que les caractéristiques physiques des étoiles varient énormément, de sorte qu’il est facile, comme nous le verrons bientôt, de raconter une histoire sensationnelle en contrastant les extrêmes, en opposant les plus brillants aux plus faibles, les plus grands aux plus petits, et ainsi de suite. Cela donnerait cependant une image très injuste des habitants du ciel ; ce serait comme juger une nation d’après les géants et les nains, les hommes forts et les hommes à jeun, vus sous la tente du forain.
Nous obtiendrons une idée plus équilibrée du degré réel de diversité des étoiles dans leur ensemble si nous considérons les états physiques des étoiles les plus proches du Soleil. En les considérant précisément dans leur ordre d’apparition, nous évitons tout soupçon de vouloir introduire des étoiles simplement parce qu’elles sont bizarres ou exceptionnelles. On peut s’attendre à ce que le petit groupe d’étoiles ainsi obtenu constitue un échantillon représentatif des étoiles du ciel, même s’il ne sera évidemment pas suffisamment large pour inclure les extrêmes. Nous n’avons pas besoin d’aborder le Soleil lui-même en détail, car il constituera notre étoile standard, par rapport à laquelle toutes les comparaisons seront faites.
Le système des α Centauri. Ce système est constitué de trois étoiles constitutives, que l’on pense être nos trois plus proches voisines dans l’espace.
La plus brillante, α Centauri A, est très semblable au Soleil. Elle est de même couleur et de même type spectral, mais pèse 14 % de plus et est environ 12 % plus lumineuse. Étant de la même couleur que le Soleil, elle émet la même quantité de rayonnement par pouce carré. Ainsi, sa luminosité supérieure de 12 % montre que sa surface doit être 12 % plus grande, et donc son diamètre 6 % plus grand que celui du Soleil.
Le deuxième constituant, α Centauri B, est considérablement plus rouge que le soleil, sa température de surface n’étant que d’environ 4 400 degrés contre environ 6 000 degrés pour le soleil. Il possède 97 % du poids du soleil, mais seulement environ un tiers de sa luminosité. Pourtant, en raison de sa basse température, il lui faut 50 % de surface de plus que le soleil pour émettre un tiers du rayonnement solaire ; cela rend son diamètre 22 % plus grand que celui du soleil. α Centauri A et α Centauri B forment ensemble une binaire visuelle, les deux composants tournant l’un autour de l’autre sur une période de 79 ans.
Aucun de ces deux éléments n’est très différent du Soleil, mais la troisième étoile du système, Proxima du Centaure, est d’un type totalement différent. De couleur rouge, sa température de surface n’est que d’environ 3 000 degrés. Extrêmement faible, elle n’émet qu’un dix-millième de la lumière du Soleil et son diamètre n’est que d’un quatorzième de celui-ci. Son poids est inconnu.
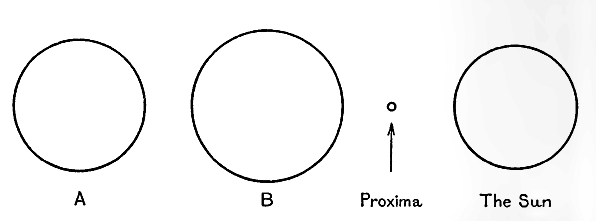
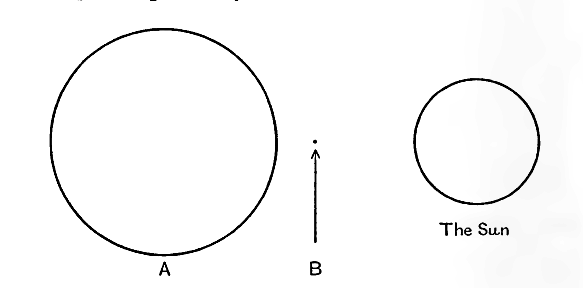
Les dimensions des trois étoiles de ce système, avec celle du soleil à titre de comparaison, sont indiquées dans la figure 17.
Munich 15040. Il s’agit d’une étoile unique, faible, dont on sait peu de choses. Sa surface est rouge, sa température est probablement légèrement supérieure à 2 500 degrés, et elle n’émet que ième de la lumière du Soleil.
Wolf 359. C’est l’étoile la plus faible jamais découverte, mais on en sait très peu à son sujet. Elle est rouge et n’émet qu’environ ième de la lumière du Soleil.
[ p. 265 ] Lalande 21185. Une autre étoile rouge faible, émettant ième de la lumière du soleil.
Le système de Sirius. Il se compose de deux étoiles très différentes, et l’on soupçonne qu’une troisième pourrait également exister.
L’étoile principale, Sirius A, qui apparaît comme l’étoile la plus brillante du ciel (l’étoile du Chien), est blanche et sa température de surface est d’environ 11 000 degrés. Cette température étant presque deux fois supérieure à celle du Soleil, Sirius A émet près de 16 fois plus de rayonnement par pouce carré que le Soleil. Sa luminosité est environ 26 fois supérieure à celle du Soleil, ce qui nécessite un diamètre de l’étoile supérieur de 58 % à celui du Soleil. Son volume est près de quatre fois supérieur à celui du Soleil, mais son poids n’est que de 2,45 fois supérieur, de sorte que la matière n’est pas aussi dense dans Sirius A que dans le Soleil. Un mètre cube moyen contient 1,42 tonne dans le Soleil, mais seulement 0,93 tonne dans Sirius A.
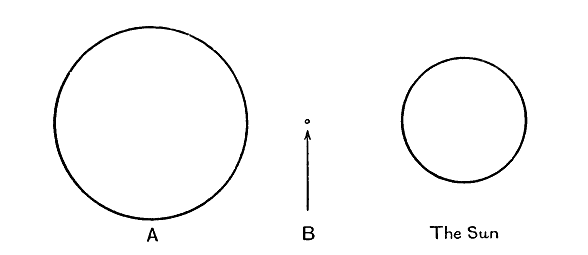
La faible compagne Sirius B est l’une des étoiles les plus intéressantes du ciel. Elle est presque de la même couleur et du même type spectral que Sirius A, mais n’émet qu’un dix-millième de lumière. Après avoir pris en compte la légère différence de température de surface, nous constatons [ p. 266 ] que sa surface n’est que ième et son diamètre ième de celui de Sirius A. Pourtant, Sirius A ne pèse que trois fois plus que Sirius B, bien qu’elle ait 125 000 fois son volume. Ce n’est pas Sirius A, mais Sirius B qui est remarquable ; la densité moyenne de matière dans cette dernière est environ 60 000 fois celle de l’eau, le pouce cube moyen contenant près d’une tonne de matière. La figure 18 montre les dimensions des deux composantes de Sirius, dessinées à la même échelle que fig. 17.
B.D. 12° 4523 et Innes 11 h. 12 m., 57,2°. Deux étoiles dont on ne connaît pas l’état physique, si ce n’est qu’elles sont très faibles, émettant respectivement e et la lumière du soleil.
Cordoba 5 h. 343 et τ Ceti. Deux étoiles faibles, toutes deux de couleur rougeâtre, émettant respectivement et un tiers de la lumière du soleil.
Le système de Procyon. C’est un système binaire, semblable à bien des égards à Sirius. L’étoile principale, Procyon A, est du même type que le Soleil, mais pèse 24 % de plus et émet 5,5 fois plus de lumière. Sa température de surface est d’environ 7 000 degrés et son diamètre est 1,80 fois celui du Soleil.
Son compagnon, Procyon B, est si faible que l’on ne connaît rien de sa condition physique, si ce n’est qu’il n’émet que 130 000 ième de la lumière du Soleil. Son poids représente 39 % de celui du Soleil.
Fig. 19 montre les tailles des deux composants de Procyon à la même échelle que précédemment.
Viennent ensuite, à mesure que nous nous éloignons du Soleil, huit étoiles très peu distinctes, chacune plus rouge et plus faible que le Soleil, aucune d’elles n’ayant une température de surface supérieure à 5 000 degrés et n’émettant pas plus d’un quart de la lumière solaire. Viennent ensuite
Le système de Kruger 60. Il s’agit d’un système binaire dans lequel les deux composantes sont petites, rouges et faibles.

Le composant le plus brillant, Kruger 60 A, a une température de surface de 3 200 degrés et émet ième de la lumière du Soleil. Son diamètre est un tiers et son poids un quart de celui du Soleil ; sa substance doit donc être environ sept fois plus compacte que celle du Soleil. Le composant le plus faible, Kruger 60 B, a une température de surface similaire, mais n’émet que ième de la lumière du Soleil. Son diamètre est un sixième et son poids un cinquième de celui du Soleil ; sa substance doit donc être environ quarante fois plus compacte que celle du Soleil. Le système est illustré dans la fig. 20.
Étoile de van Maaneri. Une autre étoile très faible, dont la température de surface est élevée (7 000 degrés). Malgré cela, elle n’émet que ième de la lumière solaire. Par conséquent, son diamètre n’est que d’environ ième de celui du Soleil, l’étoile étant plus petite que la Terre. Son poids est inconnu, mais sa matière est probablement encore plus dense que celle de Sirius B.
L’analyse de cet échantillon d’étoiles suggère que la majorité des étoiles dans l’espace sont plus petites, plus froides et plus faibles que le Soleil. Il existe des étoiles bien plus brillantes que le Soleil, mais elles sont exceptionnelles : l’étoile moyenne dans le ciel est petite et terne comparée à notre Soleil.
Avec cet échantillon de la population moyenne du ciel sous les yeux, nous pouvons aborder les différentes caractéristiques des étoiles de manière systématique, sans craindre de mentionner les extrêmes. Commençons par leur poids.
Poids stellaire. Les deux étoiles de plus faible poids connu dans tout le ciel sont la faible composante de Kruger 60, dont nous venons de parler, et la plus faible composante du système triple ο2 Eridani, chacune ayant un cinquième du poids du Soleil. Mais les étoiles dont les poids sont connus sont si peu nombreuses qu’il est impossible de supposer qu’elles soient les plus faibles poids que l’on puisse trouver dans tout l’univers stellaire. Un aperçu général de la situation, sur des lignes qui seront indiquées plus loin ([#p281]), suggère qu’il pourrait y avoir de nombreuses étoiles de poids encore plus faible, mais que très peu d’entre elles sont susceptibles d’avoir des poids énormément plus petits. Probablement très peu d’étoiles pèsent aussi peu qu’un dixième du poids du Soleil.
La grande majorité des étoiles ont des poids intermédiaires entre ce poids et dix fois celui du Soleil. Les étoiles pesant même trois fois plus que le Soleil sont rares, celles qui pèsent dix fois plus sont très rares, probablement seulement une étoile sur 100 000 ayant dix fois le poids du Soleil. Des poids encore plus élevés existent sans aucun doute – nous avons déjà mentionné l’étoile de Plaskett, dont les deux constituants pèsent respectivement plus de 75 et 63 fois le poids du Soleil, et le système quadruple 27 Canis Majoris qui, selon toute apparence, pèse 940 fois le poids du Soleil – mais de tels cas sont très, très rares. On peut dire qu’en règle générale, le poids des étoiles se situe entre un dixième et dix fois celui du Soleil, et nous constaterons que les étoiles diffèrent moins par leur poids que par la plupart de leurs autres caractéristiques physiques.
Luminosité. Une gamme bien plus vaste est montrée, par exemple, dans les luminosités des étoiles – dans leurs puissances en bougies mesurées en termes de puissance en bougies du Soleil comme unité. L’étoile la plus lumineuse connue est S Doradus, déjà mentionnée, avec une luminosité 300 000 fois supérieure à celle du Soleil, tandis que la moins lumineuse est Wolf 359 avec seulement un cinquante-millième de la luminosité du Soleil. La gamme des luminosités stellaires, comme des poids stellaires, s’étend à peu près également des deux côtés du Soleil, de sorte que le Soleil est plutôt une étoile moyenne en ce qui concerne à la fois le poids et la luminosité. Elle est moyenne dans le sens où elle se situe à mi-chemin entre les extrêmes, mais nous avons vu qu’il y a beaucoup plus d’étoiles en dessous qu’au-dessus.
[ p. 270 ] Comparée à la gamme très modérée des poids stellaires, la gamme de luminosité est énorme ; S Doradus est 15 000 000 000 de fois plus lumineuse que Wolf 359. Si S Doradus est un phare, Wolf 359 est un peu moins qu’une luciole, le soleil étant une bougie ordinaire. Si le soleil commençait soudainement à émettre autant de lumière et de chaleur que S Doradus, la température de la Terre et de tout ce qui s’y trouve monterait à environ 7 000 degrés, de sorte que nous et la Terre solide disparaîtrions dans un nuage de vapeur. D’un autre côté, si l’émission de lumière et de chaleur du soleil devait soudainement chuter à celle de Wolf 359, les gens à l’équateur terrestre constateraient que leur nouveau soleil ne donne qu’autant de lumière et de chaleur à midi qu’un feu de charbon à un mile de distance ; Nous serions tous gelés, tandis que l’atmosphère terrestre nous entourerait comme un océan d’air liquide. À notre connaissance, il est impossible que le Soleil se comporte soudainement comme S Doradus, mais nous verrons plus loin que la possibilité qu’il se comporte comme Wolf 359 n’est pas entièrement un rêve illusoire.
Température de surface et rayonnement. Sirius est la plus haute température de surface de toutes les étoiles proches du Soleil ; elle est d’environ 11 000 degrés, soit près du double de celle du Soleil. En allant plus loin, on trouve de nombreuses étoiles dont la température de surface est bien plus élevée. Par exemple, l’étoile de Plaskett est créditée d’une température de 28 000 degrés, même s’il faut admettre qu’une part importante d’incertitude entre dans toute estimation de températures stellaires très élevées.
À l’autre extrême, les températures stellaires descendant jusqu’à environ 2 500 degrés sont relativement courantes. Les températures les plus basses sont confinées aux étoiles variables [ p. 271 ] d’un type très particulier (variables à longue période) dans lesquelles la variation de luminosité s’accompagne d’une variation de la température de la surface de l’étoile, et en est d’ailleurs principalement la cause. La température de ces étoiles, lorsqu’elle est au plus bas, descend jusqu’à 1 650 degrés, ce qui est à peine supérieur à la température d’un feu de charbon ordinaire. Chez beaucoup d’entre elles, la température varie sur une large plage, mais elle ne descend jamais au point de rendre l’étoile complètement invisible. Il existe donc une plage de température inférieure à environ 2 500 degrés qu’aucune étoile n’est connue pour occuper, à l’exception des variables à longue période qui n’y pénètrent que par intervalles. Cela semble suggérer que le nombre d’étoiles absolument sombres dans le ciel est relativement faible. D’autres éléments de preuve mènent à la même conclusion. Si une étoile cessait de briller, son attraction gravitationnelle trahirait encore son existence. Bien que nous ne puissions détecter une seule étoile sombre de cette manière, nous pourrions en détecter une multitude. Si une grande proportion d’étoiles étaient sombres, nous devrions probablement suspecter leur existence d’après leurs effets sur le mouvement des autres, de sorte que des considérations gravitationnelles générales excluent la possibilité d’un grand nombre d’étoiles sombres.
D’après nos connaissances actuelles, la température des surfaces stellaires varie, en général, d’environ 30 000 degrés à environ 2 500 degrés, la limite inférieure étant étendue à environ 1 650 degrés pour les variables à longue période à leurs températures les plus basses.
Hormis les variables de longue période, il ne s’agit que d’un écart de 12 à 1, de sorte que les températures des étoiles sont plus uniformes que leurs luminosités ou leurs poids. Il faut cependant se rappeler que le rayonnement par pouce carré d’une étoile est bien plus fondamental que sa température de surface, et qu’un écart de 12 à 1 [ p. 272 ] pour cette dernière implique un écart de plus de 20 000 à 1 pour la première. Si l’on inclut les variables de longue période, l’écart d’émission de rayonnement par pouce carré est d’environ 110 000 à 1.
En termes de puissance, le Soleil émet 50 chevaux-vapeur par pouce carré ; une étoile dont la température de surface est de 1 650 degrés n’en émet que 0,35 cheval-vapeur par pouce carré, tandis que l’étoile de Plaskett, dont la température de surface est de 28 000 degrés, en émet environ 28 000. En clair, chaque pouce carré de cette dernière étoile dégage suffisamment d’énergie pour maintenir un paquebot transatlantique à pleine vitesse, heure après heure, siècle après siècle. Et l’énergie émise par pouce carré par la surface de diverses étoiles couvre toute la gamme, de la puissance d’un paquebot à celle d’un homme dans une barque.
Taille. Les quatre étoiles ayant le plus grand diamètre connu sont les suivantes :
| Étoile | Diamètre en termes de soleil | Diamètre en miles |
|---|---|---|
| Antarès | 450 | 390 000 000 |
| α Herculis | environ 400 | 340 000 000 |
| ο Ceti (au max.) | 300 | 260 000 000 |
| Bételgeux (moyenne) | 250 | 210 000 000 |
Tous ces diamètres ont été mesurés directement par l’interféromètre. À l’échelle utilisée dans les fig. 17 à 20, où le Soleil a environ la taille d’une pièce de six pence, le cercle nécessaire pour représenter μCéti serait aussi grand que le sol d’une pièce de bonne taille, tandis que la deuxième étoile du système (car μCéti est binaire) aurait la taille d’un grain de sable. On peut se faire une idée de l’immensité de ces étoiles en remarquant que chacun de leurs diamètres est plus grand que le diamètre de l’orbite terrestre, de sorte que si le Soleil devait atteindre la taille de l’une d’entre elles, nous nous trouverions à l’intérieur de celle-ci.
Ces étoiles doivent être extrêmement ténues. Antarès, par exemple, occupe 90 000 000 de fois plus d’espace que le Soleil ; si sa matière était aussi compacte, elle pèserait 90 000 000 de fois le Soleil. Pourtant, en réalité, son poids n’est probablement que 40 ou 50 fois supérieur à celui du Soleil, la différence entre ce chiffre et 90 000 000 provenant de la différence de densité entre Antarès et le Soleil. En moyenne, une tonne de matière dans le Soleil occupe considérablement moins d’un mètre cube ; dans Antarès, elle occupe bien plus d’espace que l’intérieur de la cathédrale Saint-Paul. Pourtant, une étude détaillée des intérieurs stellaires montre que nous ne pouvons attacher que peu de signification à une moyenne de ce type. Il est fort probable que la matière au centre d’Antarès soit presque (mais pas tout à fait) aussi compacte que celle au centre du Soleil (p. 291 ci-dessous). La taille gigantesque d’Antarès est probablement due principalement à une atmosphère extrêmement étendue de gaz très ténu, et il est inutile d’établir une moyenne entre celle-ci et la matière compacte au centre de l’étoile.
Les objets mystérieux connus sous le nom de nébuleuses planétaires, dont des exemples sont présentés dans la planche II (p. 28), devraient peut-être être considérés comme des étoiles de diamètre encore plus grand. Au centre de chacune d’elles, le télescope révèle une étoile relativement faible, dont la température de surface est extrêmement élevée. Autour d’elle se trouve la nébulosité qui a donné à ces objets leur nom quelque peu malheureux. Il s’agit probablement simplement d’une atmosphère d’une étendue encore plus grande que celle qui entoure les quatre étoiles de notre tableau. Van Maanen [ p. 274 ] estime le diamètre de la nébuleuse de l’Anneau de la Lyre (fig. 2 de la planche II) à 570 fois celui de l’orbite terrestre, soit environ 170 000 000 000 de kilomètres. Cette nébulosité, cependant, diffère de l’atmosphère d’une étoile ordinaire par sa quasi-transparence ; nous pouvons voir à travers 106 000 000 000 de kilomètres de la nébuleuse de l’Anneau, mais nous ne pouvons voir que quelques dizaines ou centaines de kilomètres à l’intérieur d’une étoile ordinaire.
À l’autre extrême de la taille, la plus petite étoile connue, l’étoile de van Maanen (p. 268) est presque aussi grande que la Terre ; plus d’un million de ces étoiles pourraient être regroupées à l’intérieur du Soleil et laisser encore de la place. Et pourtant, son poids est selon toute probabilité comparable, non pas à celui de la Terre, mais à celui du Soleil ; à première vue, il pourrait peser environ un cinquième du poids du Soleil. Pour contenir un cinquième de la substance solaire dans un globe de la taille de la Terre, une tonne moyenne de matière doit être entassée dans un espace d’environ la taille d’une petite cerise – environ dix tonnes par pouce cube. La solidité de la Terre suggère que ses atomes doivent être assez serrés les uns contre les autres, mais les atomes de l’étoile de van Maanen doivent être 66 000 fois plus serrés.
Comment cela se produit-il ? Comme nous le verrons bientôt, il n’y a qu’une seule réponse possible. L’atome est principalement constitué de vide – nous avons comparé l’atome de carbone à six guêpes bourdonnant dans la gare de Waterloo. Décomposons l’atome en ses éléments constitutifs, rassemblons-les le plus étroitement possible, et nous verrons comment la matière est compactée dans l’étoile de van Maanen. Six guêpes, capables de parcourir toute la gare de Waterloo, peuvent néanmoins tenir dans une très petite boîte.
Géantes et naines. Il existe une série continue d’étoiles entre les limites de poids que nous avons [ p. 275 ] mentionnées, et il en va de même pour les limites de température (et donc aussi de couleur) et de taille.
Dans ces limites, je peux vous trouver une étoile de n’importe quel poids, couleur ou taille. Mais cela ne signifie pas que vous pouvez spécifier le poids, la couleur et la taille de l’étoile que vous souhaitez, et que je me charge de la trouver pour vous ; si le poids est correct, la couleur peut être incorrecte, et ainsi de suite. Par exemple, si vous demandez une étoile rouge, je peux vous en trouver une très lourde ou une très légère, mais il est inutile que vous demandiez une étoile de poids intermédiaire. À notre connaissance, les étoiles rouges de poids intermédiaire n’existent tout simplement pas. Il en va de même pour la taille : il n’existe pas d’étoiles rouges de taille intermédiaire. Hertzsprung remarqua [ p. 276 ] en 1905 que les étoiles rouges pouvaient être divisées en deux classes distinctes, caractérisées par une grande et une petite taille : il les appela Géantes et Naines. Russell, étudiant la question plus en détail en 1913, confirma les conclusions antérieures de Hertzsprung et montra que la division géante-naine s’étendait aux étoiles d’autres couleurs que le rouge.
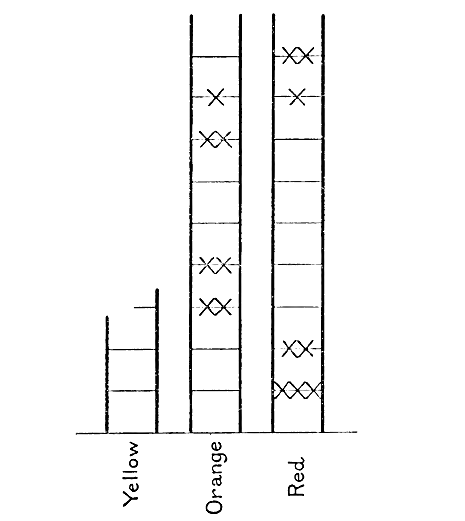
Imaginez une série d’échelles colorées, une pour chaque couleur d’étoile (rouge, orange, etc.). Prenez toutes les étoiles rouges et placez-les (en imagination) sur les différents barreaux de l’échelle rouge. Ne les placez pas au hasard ; ordonnez-les par ordre de luminosité, en plaçant celles qui ont la luminosité la plus élevée en haut. De plus, placez plusieurs étoiles sur le même barreau si leurs luminosités sont à peu près égales. Pour que la disposition soit précise, chaque barreau de l’échelle représente une luminosité cinq fois supérieure à celle de l’échelon immédiatement inférieur, de sorte que chaque barreau ait une luminosité définie qui lui est associée[3].
Forts de cet accord, nous sommes prêts à poursuivre. Nous prenons nos étoiles rouges et les plaçons chacune sur l’échelon correspondant de l’échelle rouge, et ainsi de suite pour chaque autre couleur. Le résultat est présenté schématiquement dans la fig. 21, les différentes étoiles étant représentées par des croix.
Les étoiles rouges se trouvent à droite du diagramme, la division de Hertzsprung en géantes et naines étant très clairement marquée. Les étoiles orange se trouvent à gauche de l’échelle ; comme l’a constaté Russell, la division apparaît à nouveau, mais de façon moins marquée.
Le diagramme de Russell. Réalisons des diagrammes en échelle de ce type pour chaque couleur d’étoile, et plaçons-les [ p. 277 ] côte à côte dans leur ordre approprié, de manière à représenter des étoiles de toutes les couleurs possibles. Nous obtenons un diagramme du type de celui de la figure 22. Ce type de diagramme a été introduit par Russell en 1913 et est aujourd’hui généralement connu sous le nom de diagramme de Russell.
Les lettres en haut du diagramme représentent les types spectraux des étoiles, car elles fournissent une classification plus précise et plus précise que les noms de couleurs. Les couleurs correspondant approximativement aux différents types spectraux sont indiquées en bas du diagramme.
Seuls quelques exemples d’étoiles sont représentés, mais toutes les étoiles connues se concentrent autour de ces quelques étoiles typiques. En gros, deux régions distinctes et déconnectées sont occupées par des étoiles. La première, et la plus importante, est une région en forme de Y inversé : la ligne centrale de cette région est marquée par une ligne épaisse continue, d’après la détermination de sa position par Redman. La seconde région, plus petite, se trouve près du coin inférieur gauche du diagramme. Les étoiles qui occupent cette région sont très faibles et ont des températures de surface bien plus élevées que celles des étoiles de luminosité similaire.
Nous avons déjà vu comment calculer le diamètre d’une étoile à partir de sa température de surface et de sa luminosité. Cela revient à dire que deux étoiles occupant la même position dans le diagramme de Russell doivent avoir le même diamètre. Ainsi, un diamètre défini est associé à chaque point du diagramme, et nous pouvons y représenter les diamètres stellaires, tout comme nous pouvons représenter les altitudes au-dessus du niveau de la mer sur une carte géographique, par un système de courbes de niveau. Dans le cas présent, ces courbes se révèlent être un système de courbes presque parallèles. Celles-ci se situent approximativement comme le montrent les lignes pointillées de la figure 22, toutes les étoiles situées sur une même ligne ayant le même diamètre.
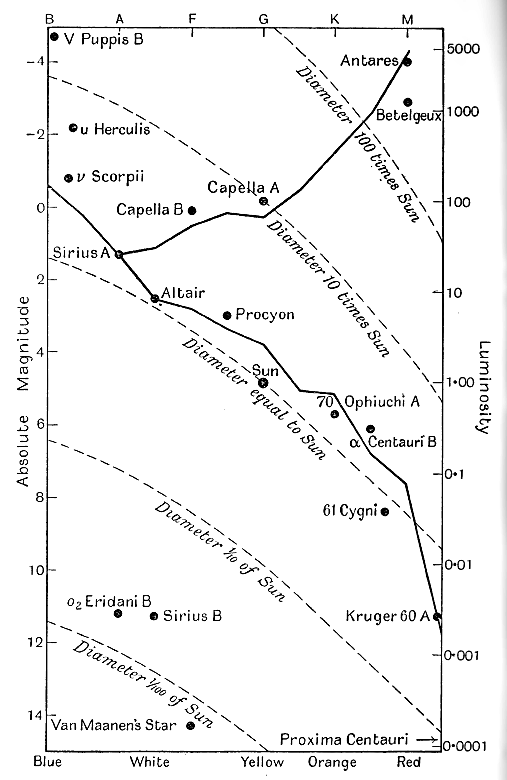
Ce diagramme éclaire la question générale des diamètres stellaires. On constate immédiatement que les étoiles de plus grand diamètre – 100 fois celui du Soleil ou plus – sont nécessairement des étoiles rouges de forte luminosité. En réalité, les étoiles de grand diamètre présentées dans le tableau p. 272 sont toutes rouges et ont une luminosité très élevée ; ce sont des géantes rouges.
La majorité des étoiles du ciel se situent dans la ceinture qui traverse le diagramme de la fig. 22 du coin supérieur gauche au coin inférieur droit. C’est ce qu’on appelle la « séquence principale ». La position de cette bande par rapport aux « courbes de niveau » des diamètres montre que les étoiles de la séquence principale ont des diamètres modérés. Les plus brillantes peuvent avoir un diamètre vingt fois supérieur à celui du Soleil, tandis que les plus faibles peuvent n’en avoir qu’un vingtième environ, mais elles ont toutes des diamètres au moins comparables à celui du Soleil. L’échantillon d’étoiles proches du Soleil, déjà évoqué, fournit de nombreux exemples d’étoiles de la séquence principale ; nous avons, par ordre de luminosité décroissante :
| Étoile | Luminosité | Diamètre (par rapport au soleil) |
|---|---|---|
| Sirius A | 26,3 | 1,58 |
| Procyon A | 5,5 | 1,80 |
| α Centaure A | 1.12 | 1,07 |
| Dim | 1.00 | 1.00 |
| α Centaures B | 0,32 | 1.22 |
| τ Ceti | 0,32 | 0,95 |
| ε Indi | 0,15 | 0,82 |
| Kruger 60 A | 0,0026 | 0,33 |
| Kruger 60 B | 0,0007 | 0,17 |
| Loup 359 | 0,00002 | 0,03 |
[ p. 280 ] Ce tableau montre clairement comment la luminosité et le diamètre stellaires diminuent ensemble à mesure que nous parcourons la séquence principale.
Le groupe d’étoiles restant dans la fig. 22, celles situées en bas à gauche, sont généralement appelées « naines blanches ». Leur position sur le diagramme indique que leur diamètre doit être excessivement petit. Le voisinage du Soleil fournit trois exemples de cette classe d’étoiles, comme le montre le tableau suivant :
| Étoile | Luminosité | Diamètre (par rapport au soleil) |
|---|---|---|
| Sirius B | 0,0026 | 0,03 |
| ο2 Éridani B | 0,0031 | 0,018 |
| l’étoile de van Maanen | 0,00016 | 0,009 |
En plus de ces étoiles, la faible compagne d’μmicron Ceti est certainement une naine blanche, tandis que Procyon B pourrait l’être. Ce sont les seuls exemples connus de naines blanches, mais leur extrême faiblesse les rend très difficiles à détecter, ce qui laisse supposer qu’il s’agit d’objets assez fréquents dans l’espace.
Dans le tableau p. 279, les étoiles de la séquence principale étaient censées être classées par ordre de luminosité, mais il se trouve que cet ordre correspond également à celui des poids. Les poids de trois étoiles sont inconnus ; ceux des autres sont les suivants :
| Étoile | Luminosité | Poids (en termes de soleil) |
|---|---|---|
| Sirius A | 26,3 | 2,45 |
| Procyon A | 5,5 | 1,24 |
| α Centaure A | 1.12 | 1.14 |
| Dim | 1.00 | 1.00 |
| α Centaures B | 0,32 | 0,97 |
| Kruger 60 A | 0,0026 | 0,25 |
| Kruger 60 B | 0,0007 | 0,20 |
[ p. 281 ] Comme les luminosités, les poids diminuent régulièrement à mesure que nous parcourons la séquence principale, bien que, comme nous l’avons déjà remarqué, le poids diminue beaucoup moins rapidement que la luminosité.
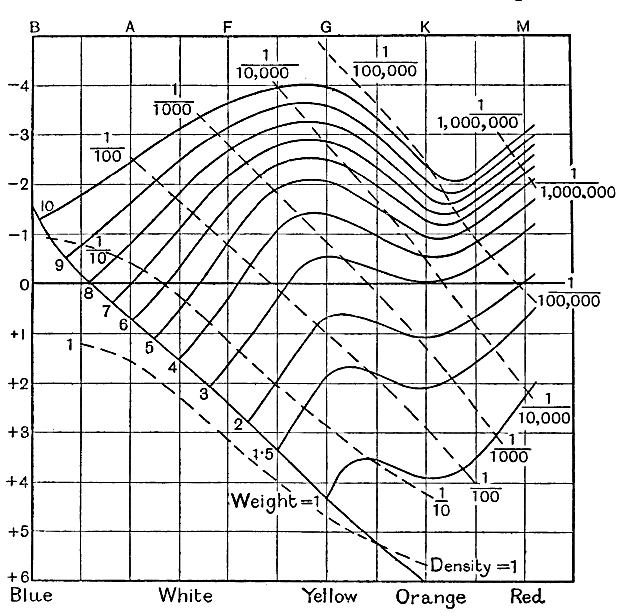
Les seules étoiles dont le poids peut être mesuré directement sont les composantes des systèmes binaires, et celles-ci sont relativement peu nombreuses. Seares a cependant constaté que le poids des systèmes binaires était conforme à la loi d’équipartition de l’énergie, déjà expliquée au Chapitre III, de sorte qu’il est hautement probable que d’autres étoiles, non binaires, s’y conforment également, car il est difficile d’imaginer une raison pour laquelle les systèmes binaires atteindraient un état d’équipartition plus tôt que les autres étoiles. On se rappellera que cet état est défini par une loi purement statistique reliant le poids et la vitesse de mouvement des étoiles. Ainsi, le fait qu’un système d’étoiles ait atteint cet état ne peut donner aucune information sur le poids d’une étoile individuelle dont la vitesse est connue, mais permet de déterminer le poids moyen de tout groupe d’étoiles en fonction de leur vitesse moyenne de mouvement. Seares a ainsi déterminé les poids moyens d’étoiles de luminosités et de types spectraux différents, autrement dit les poids moyens des étoiles représentées aux différents points du diagramme de la fig. 22. Les résultats obtenus sont illustrés par les courbes épaisses de la fig. 23. La disposition de ces courbes confirme les conclusions tirées de quelques étoiles sélectionnées : le poids des étoiles de la séquence principale diminue régulièrement à mesure que l’on descend dans la séquence, de la luminosité élevée à la luminosité faible.
Ces lignes courbes indiquent le poids moyen des étoiles représentées en chaque point du diagramme de Russell, et leurs diamètres sont déjà connus grâce à la fig. 22. À partir de ces deux données, la densité moyenne de l’étoile [ p. 282 ] peut bien sûr être calculée. Les densités moyennes calculées par Seares sont représentées par les lignes pointillées de la fig. 23.
Ceci complète notre collection de données d’observation. Nous abordons maintenant le problème, bien plus difficile, de la compréhension de tout cela. Nous quittons ici le terrain solide des faits avérés pour pénétrer dans les bourbiers obscurs des conjectures, des hypothèses et des spéculations. Les questions que nous allons aborder comptent parmi les plus intéressantes de toute l’astronomie, et force est de constater que la science n’a jusqu’à présent obtenu que des réponses lamentablement poussiéreuses. Le lecteur avide de certitudes préférera peut-être lire autre chose que le reste de ce chapitre.
¶ La condition physique des étoiles
Les données d’observation précédentes ont fourni de nombreuses preuves de l’inexistence d’étoiles répondant à certaines spécifications. Autrement dit, certaines régions du diagramme de Russell sont totalement inoccupées.
Pour prendre l’exemple le plus frappant, il n’y a aucune étoile à gauche de la séquence principale dans le diagramme de Russell (fig. 22), jusqu’au groupe assez isolé des naines blanches. Pourquoi n’y a-t-il aucune étoile dans des conditions intermédiaires ? Pourquoi, pour rendre l’exemple encore plus précis, n’existe-t-il aucune étoile de la même couleur que Sirius, mais avec seulement un dixième de sa luminosité ? Pourquoi faut-il descendre jusqu’à la naine blanche o µ2 Eridani B, dont la luminosité n’est qu’un dix-millième de celle de Sirius, avant de trouver une étoile dont la couleur corresponde à celle de Sirius ?
Une hypothèse qui vient naturellement à l’esprit est que les étoiles de la séquence principale et les naines blanches pourraient former des groupes distincts car elles sont d’âges totalement différents ; elles pourraient représenter des créations distinctes. À mesure que les étoiles vieillissent, leur poids et leur luminosité diminuent, de sorte qu’il est naturel d’interpréter la faible masse et la luminosité extrêmement faible des naines blanches comme la preuve d’un âge bien supérieur à celui des étoiles normales de la séquence principale. Pourtant, cette hypothèse ne semble pas soutenable.
Français À la seule exception de l’étoile de van Maanen, toute étoile connue ou suspectée d’être [ p. 284 ] une naine blanche forme une composante d’un système binaire, et dans chaque cas, sa compagne est une étoile de la séquence principale ou (dans le cas d’ο Ceti) une géante rouge. Nous avons déjà vu combien il est rare que deux étoiles se rapprochent l’une de l’autre dans l’espace. Ce doit être un événement presque inconcevablement rare que deux étoiles, se déplaçant à l’origine comme des corps indépendants, se rencontrent au cours de leurs errances aléatoires, au point que la grande « capture » la petite, et qu’elles voyagent désormais ensemble dans l’espace. Car il peut être démontré que, pour qu’un tel événement se produise, il faut quelque chose de plus qu’un rapprochement rapproché ; Un rapprochement doit avoir lieu en présence d’une troisième étoile, de sorte que pas moins de trois étoiles doivent se rapprocher simultanément au cours de leurs pérégrinations dans les vastes espaces. Il est presque inconcevable que cela se produise en un seul cas, mais supposer que cela se soit produit pour chaque naine blanche connue sauf une est une hypothèse trop improbable. Il faut donc supposer que les naines blanches et leurs compagnes plus normales vivent ensemble depuis leur naissance, et sont donc nées simultanément de la même nébuleuse.
La différence entre les naines blanches et les étoiles de la séquence principale ne peut donc pas être une simple différence d’âge, et il semblerait qu’une raison physique milite contre l’existence d’étoiles dans des conditions intermédiaires. En adoptant une perspective plus générale, nous sommes amenés à rechercher si l’absence d’étoiles construites selon certaines spécifications peut être attribuée au fait que ces étoiles nécessitent des propriétés physiques que la nature ne peut leur fournir. Cela nous amène directement à la question générale de la structure et du mécanisme des étoiles. [ p. 285 ]
¶ La constitution interne des étoiles
La plupart des recherches sur la structure des étoiles ont été menées en partant du principe que leur intérieur est entièrement gazeux. Sans accepter cette hypothèse comme une vérité absolue, nous pouvons l’adopter pour le moment, pour la simple raison qu’elle constitue la voie d’approche la plus pratique face à un problème excessivement complexe.
Un théorème mathématique, généralement connu sous le nom de théorème de Poincaré, s’avère extrêmement utile pour analyser l’état interne d’une étoile gazeuse. Nous avons vu comment Helmholtz pensait que l’énergie du rayonnement solaire pouvait provenir de la contraction du Soleil, chaque couche s’effondrant sur la couche interne suivante à mesure que cette dernière se contractait, transformant l’énergie libérée par sa chute en chaleur et en lumière. Il est facile d’estimer la quantité d’énergie libérée par une telle contraction. Par exemple, Lord Kelvin a calculé que la contraction du Soleil, en passant d’une taille infinie à son diamètre actuel de 1390 000 kilomètres, libérerait environ autant d’énergie que le Soleil rayonne actuellement en 50 millions d’années. Exprimé en ergs, le rétrécissement du Soleil libérerait 6 x 1048 ergs d’énergie.
Le théorème de Poincaré stipule que l’énergie totale de mouvement de toutes les molécules d’une étoile gazeuse, quelle qu’elle soit, est exactement égale à la moitié de l’énergie totale que l’étoile aurait libérée en rétrécissant jusqu’à sa taille actuelle. Ce théorème est vrai, que l’étoile ait ou non rétréci : seul son état actuel est en jeu.
Une conséquence intéressante est que plus une étoile gazeuse rétrécit, plus elle devient chaude ; si une étoile [ p. 286 ] rétrécit jusqu’à la moitié de sa taille actuelle, l’énergie totale libérée par sa réduction de taille infinie est doublée, de sorte que l’énergie totale de mouvement de ses molécules est doublée, et donc sa température moyenne est doublée. Il s’agit d’un cas particulier de ce que l’on appelle généralement la loi de Lane.
Poursuivons nos calculs pour le cas particulier du Soleil. Le théorème de Poincaré nous apprend que, si le Soleil est gazeux, l’énergie totale de mouvement de toutes ses molécules est de 3 x 1048 ergs. Il s’agit ensuite de savoir combien de molécules le Soleil contient. Son poids est de 2 x 1033 grammes, mais combien de molécules y a-t-il par gramme ? La réponse dépend bien sûr du type de molécule concerné : il y a 3 x 1023 molécules dans un gramme d’hydrogène, 2 x 1022 dans un gramme d’air et seulement 2,5 x 1021 dans un gramme d’uranium.
Si l’on suppose que le Soleil est constitué d’air, il doit être composé de 4 x 1055 molécules, de sorte que l’énergie moyenne de mouvement de chaque molécule doit être de 7,5 x 10-8 ergs, ce qui représente une température moyenne, à l’intérieur du Soleil, de 375 millions de degrés. En 1907, Emden, par un calcul différent, a constaté que si le Soleil était constitué d’air, la température en son centre serait de 455 millions de degrés. Au-delà des détails, il est clair que la température intérieure d’un Soleil constitué d’air serait de l’ordre de centaines de millions de degrés.
Jusqu’à présent, toutes les études sur l’intérieur des étoiles reposaient sur l’hypothèse que les étoiles étaient constituées d’atomes complets, voire de molécules. En 1917, j’ai effectué un calcul simple, du type déjà expliqué à la p. 141, et j’ai découvert que les quanta de rayonnement circulant à de telles températures seraient suffisamment énergétiques non seulement pour décomposer les molécules d’air en atomes, mais aussi pour les dépouiller de tous, ou presque, leurs électrons. À de telles températures, chaque molécule d’air se décomposerait en ses noyaux et électrons constitutifs aussi sûrement que, par une chaude journée, un morceau de glace se décompose en ses molécules constitutives. Les forces électriques qui, dans un environnement plus calme, réuniraient les électrons et les noyaux, d’abord en atomes, puis en molécules complètes, se trouvent impuissantes face à la grêle incessante de projectiles rapides et aux coups dévastateurs de quanta de haute énergie ; ce serait comme tenter de construire un château de cartes dans un ouragan. Un soleil composé de molécules d’air se révèle être une incohérence, une contradiction ; notre hypothèse s’est effondrée, et il faut tout reprendre à zéro.
Nous pouvons commencer où bon nous semble, mais la conclusion à laquelle nous devons parvenir est que, quelle que soit la nature des molécules composant le Soleil, la chaleur au centre du Soleil les décompose, complètement ou presque, en leurs noyaux et électrons constitutifs. Il en va de même pour toutes les autres étoiles, ce qui simplifie considérablement le problème de la constitution interne des étoiles. On ne peut déterminer le nombre de molécules complètes dans un gramme sans connaître leur nature. Mais si l’on décompose ces molécules en leurs éléments constitutifs, on connaît immédiatement le nombre total d’éléments constitutifs, noyaux et électrons, qui composent un gramme. En effet, les poids atomiques de tous les éléments, à l’exception de l’hydrogène, sont presque le double de leur numéro atomique (p. 110). Ainsi, comme l’a souligné Eddington, le nombre total de noyaux et de protons dans un atome entièrement fragmenté de toute substance, à l’exception de l’hydrogène, doit être égal à environ la moitié du poids atomique [ p. 288 ] de l’atome. Nous pouvons probablement négliger la possibilité qu’une étoile soit constituée en grande partie d’hydrogène. Si tel est le cas, le nombre de parties constituantes dans un gramme de matière stellaire entièrement fragmentée doit être d’environ 3 x 1023, quel que soit le type de molécule dont ces parties proviennent. Et lorsque nous connaissons le nombre total de ces parties dans une étoile, il devient facile de calculer la température intérieure de l’étoile, soit à partir du théorème de Poincaré mentionné précédemment, soit autrement. La température sera la même que si l’étoile était constituée de molécules d’hydrogène intactes.
Emden a calculé en 1907 que la température centrale d’un tel soleil serait d’environ 31 500 000 degrés. Des calculs ultérieurs, plus précis, d’Eddington ont abouti à une température presque identique, mais certains de mes calculs, plus récents encore, donnent le chiffre nettement plus élevé de 55 000 000 degrés. Il est inutile pour l’instant de discuter lequel de ces chiffres est le plus proche de la vérité. Leur diversité indiquera le degré d’incertitude associé à tous les calculs de ce type.
Il est facile de comprendre la nécessité physique de cette température élevée. La chaleur qui s’échappe de la surface du soleil doit d’abord y avoir été apportée de l’intérieur. La chaleur ne circule que d’un endroit chaud vers un endroit plus frais, et un flux de chaleur vigoureux témoigne d’un gradient de température important. La température doit augmenter brusquement à mesure que l’on passe de la surface du soleil à son centre, et cette augmentation, poursuivie sur les 700 000 kilomètres qui le séparent du centre, doit entraîner une température très élevée.
La température centrale calculée de 30 à 60 millions de degrés dépasse tellement notre expérience qu’il est difficile d’en comprendre la signification. Imaginons que nous gardions un millimètre cube de matière ordinaire – un morceau de la taille d’une tête d’épingle ordinaire – à une température de 50 000 000 degrés, soit la température approximative au centre du soleil. Aussi incroyable que cela puisse paraître, le simple maintien de cette tête d’épingle de matière à une telle température – c’est-à-dire pour reconstituer l’énergie qu’elle perd par rayonnement de ses six faces – nécessiterait toute l’énergie générée par un moteur de trois milliards de chevaux-vapeur ; la tête d’épingle de matière émettrait suffisamment de chaleur pour tuer quiconque s’aventurerait à moins de mille milles d’elle.
Aussi élevée que soit cette température, les calculs montrent qu’elle ne suffirait pas à briser complètement les molécules stellaires. Elle priverait les atomes de tous leurs électrons jusqu’aux anneaux K (p. 134), mais ceux-ci resteraient intacts. Il faut des températures encore plus élevées que celles que nous envisageons actuellement pour extraire les électrons des anneaux K du noyau d’un atome. Ce résultat est vrai pour toute la plage, d’environ 30 à 60 millions de degrés, dans laquelle la température du centre du Soleil est susceptible de se situer, et il est vrai presque indépendamment du poids atomique ou du numéro atomique des atomes dont nous supposons que le Soleil est constitué.
Ainsi, si le Soleil est entièrement gazeux, ses parties centrales doivent être constituées d’un ensemble d’atomes réduits à leurs cycles K, mais pas au-delà, volant indépendamment comme les molécules d’un gaz, et avec eux, également volant comme les molécules d’un gaz, tous les électrons arrachés qui formaient à l’origine les cycles L, M, etc. des atomes, le tout étant à une température comprise entre 30 et 60 millions de degrés. En s’éloignant vers la surface du Soleil, nous atteignons des températures plus basses, auxquelles les atomes [ p. 290 ] sont moins complètement fragmentés. Enfin, près de la surface du Soleil, nous pouvons rencontrer des atomes complètement formés, à l’exception peut-être d’un ou deux de leurs électrons les plus externes. À la surface des étoiles les plus froides, on trouve même des molécules complètes, comme par exemple les molécules d’oxyde de titane et d’hydrure de magnésium, qui apparaissent dans les spectres des étoiles rouges.
Lorsque l’on étudie la constitution interne des autres étoiles de la même manière, on constate que toutes les étoiles de la séquence principale ont à peu près la même température centrale que le Soleil. De plus, ce n’est pas leur seule propriété commune. La Fig. 23, qui présente les calculs de Seares sur les densités stellaires moyennes, montre que les densités moyennes des étoiles de la séquence principale sont toutes approximativement identiques, à l’exception de quelques écarts relativement faibles aux deux extrémités.
La densité moyenne du Soleil est de 1,4, ce qui signifie qu’un mètre cube moyen dans le Soleil contient 1,4 tonne de matière. Au centre du Soleil, la densité est environ 100 fois supérieure, de sorte qu’un mètre cube contient environ 140 tonnes de matière. À titre de comparaison, un mètre cube de plomb n’en contient qu’environ 11 tonnes. Si toutes les étoiles étaient construites sur le même modèle que le Soleil, deux étoiles ayant la même densité moyenne auraient également des densités égales en leur centre. Mais dans les étoiles ayant plusieurs fois le poids du Soleil, un nouveau facteur entre en jeu : la pression de rayonnement, la pression qu’exerce le rayonnement en raison du poids qu’il transporte. Dans la plupart des étoiles, cette pression est insignifiante comparée à la pression produite par l’impact des atomes et des électrons matériels, mais dans les étoiles très massives, elle est suffisamment importante pour influencer la structure de l’étoile. C’est à cela que [ p. 291 ] les étoiles très massives dont les diamètres sont indiqués dans le tableau p. 272 doivent leur taille anormalement grande. C’est une conséquence générale des effets perturbateurs de la pression de radiation que le poids d’une étoile très massive est beaucoup plus concentré dans ses régions centrales que celui d’une étoile plus légère, de sorte que si une étoile légère et une étoile massive ont la même densité moyenne, cette dernière aura de loin la densité la plus élevée en son centre. Lorsque ce facteur perturbateur est pris en compte, toutes les étoiles de la partie supérieure de la séquence principale se trouvent avoir approximativement les mêmes densités dans leurs régions centrales, une densité à peu près égale à celle du centre du Soleil, que nous pouvons estimer à 140 tonnes par mètre cube. Et nous avons déjà vu que les régions centrales de ces étoiles ont également approximativement les mêmes températures que le centre du Soleil, d’où il s’ensuit que leurs conditions physiques sont toutes sensiblement les mêmes. Ainsi, les atomes des régions centrales de toutes ces étoiles doivent être décomposés dans la même mesure que ceux des régions centrales du Soleil. Les anneaux électroniques K subsistent intacts, mais les anneaux extérieurs se transforment en une pluie d’électrons volant comme des molécules indépendantes.
Avec une précision suffisante pour notre propos actuel, on peut supposer que toutes les étoiles de la séquence principale, à l’exception peut-être de celles situées à son extrémité inférieure, présentent les mêmes conditions physiques. De ce fait, la séquence principale constitue une base de référence admirable pour une étude du diagramme de Russell concernant les conditions physiques des intérieurs stellaires.
Fig. 22 montre qu’une étoile à droite de la séquence principale a un diamètre plus grand qu’une étoile de la séquence principale de même masse. Par conséquent, l’énergie [ p. 292 ] qu’elle émettrait en se rétrécissant jusqu’à son diamètre actuel est moindre, et donc son énergie moléculaire de mouvement est moindre (d’après le théorème de Poincaré). Il s’ensuit que ses températures internes sont plus basses et ses atomes moins complètement fragmentés. On a constaté que les géantes rouges comme Antarès n’avaient que des températures centrales de un à cinq millions de degrés, et leurs atomes conservent probablement intacts non seulement leurs anneaux électroniques K, mais aussi leurs anneaux L et au moins une partie de leurs anneaux M.
À gauche de la séquence principale, nous trouvons une région où les étoiles, si elles existaient, auraient davantage rétréci, et donc eu des températures plus élevées et des atomes plus fragmentés. En réalité, on ne rencontre aucune étoile avant les naines blanches. Les calculs montrent que la température centrale de ces dernières doit atteindre au moins plusieurs centaines de millions de degrés, et que leurs atomes doivent être dépouillés de leurs électrons jusqu’aux noyaux. À l’exception d’un petit nombre d’atomes qui ont pu échapper à ce sort général, la matière stellaire doit être constituée de noyaux complètement dépouillés et d’électrons libres, tous traversant l’étoile indépendamment. Les fortes densités de ces étoiles fournissent une preuve convaincante de l’exactitude de ce résultat. La densité moyenne de Sirius B est certainement supérieure à 50 000, tandis que celle de l’étoile de van Maanen est probablement supérieure à 300 000. Il n’existe aucun moyen de compacter la matière de manière aussi compacte, si ce n’est en dépouillant les atomes de leurs électrons jusqu’à leurs noyaux nus.
L’impression générale la plus claire que nous pouvons nous faire du diagramme de Russell en termes de condition physique est probablement obtenue comme suit :
Nous pensons d’abord à deux bandes détachées d’étoiles : l’une, le groupe des naines blanches, formé d’étoiles dans lesquelles tous les électrons sont arrachés aux atomes ; et l’autre, la séquence principale, formée d’étoiles dans lesquelles les atomes sont encore entourés de leurs anneaux électroniques K, tandis que les anneaux extérieurs ont été arrachés. À partir du milieu de la séquence principale se trouve la branche d’éperon menant aux géantes rouges, comme le montre la fig. 22. À mesure que nous avançons, les températures internes des étoiles diminuent, de sorte que les atomes stellaires sont moins fragmentés que dans les étoiles de la séquence principale. Dans les géantes rouges à l’extrémité, même les électrons de l’anneau M peuvent encore subsister.
¶ Hypothèse de Russell
Deux explications totalement différentes de cette répartition des étoiles ont été proposées. En 1925, Russell a avancé une théorie centrée principalement sur le fait que les températures au centre des étoiles de la séquence principale sont toutes quasiment égales. Simplifions la situation un instant en imaginant qu’il soit établi que les températures au centre de toutes les étoiles sont exactement les mêmes, disons 32 000 000 degrés. Si c’était un fait certain, il serait naturel de conjecturer que les étoiles possèdent un mécanisme de contrôle par lequel elles ajustent continuellement leur température centrale à cette valeur exacte, de sorte que si la température descend en dessous de 32 000 000 degrés, le mécanisme entre en jeu et l’élève précisément à cette valeur, tandis que si elle dépasse ce chiffre, le mécanisme entre en jeu et l’abaisse. De tels mécanismes de contrôle sont bien sûr courants en ingénierie ; il y a par exemple les soupapes de sûreté qui maintiennent la pression dans une chaudière toujours uniforme, le [ p. 294 ] régulateur de Watts qui maintient un moteur toujours à la même vitesse, et le thermostat qui maintient constante la température d’une pièce.
On connaît déjà un mécanisme permettant d’élever la température au centre d’une étoile. Si une étoile ne génère aucune énergie en son sein, que ce soit par annihilation de matière ou autrement, son émission de rayonnement provoque son rétrécissement, ce qui, comme nous l’avons vu (p. 285), entraîne une élévation de sa température. Ainsi, il est facile de maintenir la température centrale d’une étoile à 32 000 000 degrés en supposant qu’aucune énergie ne soit générée tant que la température au centre est inférieure à 32 000 000 degrés, et c’est l’hypothèse principale sur laquelle repose la théorie de Russell. Il suppose qu’aucune énergie n’est générée par la matière à des températures inférieures à 32 000 000 degrés, mais que, dès que cette température est atteinte, la matière commence à s’annihiler en quantité suffisante pour assurer le rayonnement d’une étoile.
Le problème avec cette théorie est qu’il semble impossible de réguler la température depuis l’autre extrémité. Une étoile dont la température centrale est inférieure à 32 000 000 degrés doit se contracter sans générer de chaleur. La contraction ne s’arrêtera pas net dès que la température critique sera atteinte ; son élan la poursuivra jusqu’à ce que la température centrale dépasse largement 32 000 000 degrés. Dès que la température dépasse sérieusement 32 000 000 degrés au centre, celle d’une partie substantielle de l’étoile atteindra 32 000 000 degrés ou plus. L’annihilation de toute cette matière doit produire une profusion de chaleur qui élèverait encore davantage la température de l’étoile, entraînant une annihilation croissante de matière, jusqu’à ce que finalement l’étoile entière disparaisse [ p. 295 ] dans un éclair de rayonnement. En effet, la théorie de Russell suppose que la matière à 32 000 000 degrés se trouve dans un état similaire à celui de la poudre à canon à son point d’éclair. L’analyse mathématique montre alors qu’une étoile dont le centre est à une température de 32 000 000 degrés se trouverait dans l’état d’un baril de poudre à canon avec une étincelle en son centre, et — eh bien, « ohne hast, ohne rast » décrit mal la suite des événements.
Eddington a suggéré que la stabilité des étoiles pourrait être préservée en imaginant un décalage temporel entre l’instant où la matière atteint la température critique nécessaire à l’annihilation et l’instant où cette annihilation se produit. L’efficacité de ce remède n’a pas encore été prouvée, mais même si c’était le cas, d’autres difficultés subsistent. Comme l’étoile normale habite la séquence principale, Russell supposait que la matière normale avait pour propriété de s’annihiler à une température d’environ 32 000 000 degrés, la température centrale supposée uniforme de toutes les étoiles de la séquence principale. Il devint alors nécessaire d’introduire d’autres hypothèses particulières pour expliquer la luminosité des naines blanches et des étoiles de la ligne d’éperon des géantes rouges, dont le centre est à des températures très différentes de 32 000 000 degrés. Il supposa donc que ces étoiles contenaient d’autres types de matière qui se dissolvaient en rayonnement à des températures respectivement supérieures et inférieures à 32 000 000 degrés. Même si la difficulté de stabilité pouvait être surmontée, cette dernière série d’hypothèses me semble tellement artificielle qu’elle oblige à abandonner cette théorie intéressante.
Une discussion sur les difficultés de la théorie de Russell m’a conduit à entreprendre une étude mathématique de la stabilité des étoiles en général, et il s’est avéré que cela fournissait une explication simple et quelque peu inattendue de la distribution autrement incompréhensible des étoiles dans le diagramme de Russell ; en bref, les régions inoccupées du diagramme représentent des étoiles instables. J’ignore quelle proportion d’astronomes accepte cette explication ; certains, dont j’apprécie l’opinion, ne l’acceptent pas. Je ne pense pas que beaucoup de ce qui a été écrit jusqu’ici dans ce livre puisse être sérieusement remis en question par des critiques compétents, mais il est juste de dire qu’à ce stade, nous entrons en terrain controversé.
¶ L’hypothèse des étoiles liquides
Commençons par imaginer un nombre considérable d’étoiles, construites selon tous les plans possibles et à partir de toutes sortes de substances. Des recherches mathématiques montrent que certaines de ces étoiles pourraient être incapables de briller de manière stable pour l’une ou l’autre de ces deux raisons : elles pourraient exploser, comme un baril de poudre à canon chauffé à blanc, ou avoir une tendance inhérente à se contracter ou à se dilater sans limite. Qu’une étoile échappe ou non au premier écueil dépend principalement des propriétés de la substance qui la compose ; qu’elle échappe au second dépend principalement de la manière dont elle est construite. Ces deux écueils ne sont pas totalement distincts, et si l’on considère la stabilité d’étoiles entièrement gazeuses d’une masse énorme, on constate que les écueils de part et d’autre de la trajectoire se fondent en un seul, ou tout au plus qu’une étroite bande de terrain sûr les sépare. Néanmoins, on sait que des étoiles d’une masse énorme existent et continuent de briller de manière constante. Si donc ces étoiles sont entièrement gazeuses, elles doivent occuper le seul endroit sûr entre les deux fosses, et cela nous renseigne à la fois sur la manière dont elles sont construites et sur les propriétés de la substance dont elles sont construites.
Français Nous constatons que de telles étoiles n’échappent à ces deux pièges que si leur substance possède des propriétés qui paraissent très improbables et contraires à tout ce dont nous avons l’expérience ou les connaissances en physique ; en bref, pour qu’une telle étoile reste stable, l’annihilation de sa matière doit se dérouler à une vitesse qui dépend de la température. Une telle propriété semble en tout point contraire aux principes physiques expliqués au Chapitre II, comme elle l’est à toutes nos attentes concernant le comportement atomique. L’annihilation de la matière est un changement beaucoup plus violent et implique des quanta d’énergie bien plus élevés que la simple désintégration radioactive, et comme ce dernier processus n’est pas affecté par les variations de température, il semble difficilement possible que le processus d’annihilation le soit, du moins jusqu’à ce que nous atteignions des températures de l’ordre de 2 200 000 000 000 degrés indiquées dans le tableau p. 144 [4].
Nous avons cependant déjà trouvé des indications que les étoiles ne sont pas purement gazeuses, car des masses purement gazeuses ne pourraient former de systèmes binaires fermés du type observé dans les binaires spectroscopiques (p. 222). De tels systèmes ne peuvent se former qu’à partir d’une masse simulant les propriétés d’un liquide plutôt que celles d’un gaz ; la masse n’a pas besoin d’être entièrement liquide, mais il doit y avoir une divergence considérable par rapport à l’état d’un gaz pur, du moins dans ses régions centrales. D’autres preuves allant dans le même sens apparaîtront ultérieurement (pp. 310, 311).
Dès que l’on admet que l’intérieur des étoiles n’a pas besoin d’être complètement gazeux, la situation change complètement, et même un léger écart par rapport à l’état gazeux confère à l’étoile une stabilité accrue. Si une étoile de grande masse est purement gazeuse dans sa structure, la région de stabilité entre les deux pièges se réduit à une étroite bande, et ce n’est qu’en la franchissant que l’étoile peut échapper aux destins alternatifs de l’explosion ou de l’effondrement. Mais si l’étoile possède un centre liquide, ou partiellement liquide, cette bande de sécurité est si large que, conformément à la stabilité, la matière stellaire peut avoir exactement la propriété que l’on s’attendrait a priori à trouver, à savoir que son annihilation se déroule, comme la désintégration radioactive, à la même vitesse à toutes les températures. Si la substance de l’étoile possède cette propriété, elle ne risque pas d’exploser, car une masse d’uranium ou de radium n’explose pas, quoi qu’on lui fasse subir. Et l’analyse mathématique montre que si le centre de l’étoile est liquide, ou partiellement liquide, il n’y a aucun risque d’effondrement ; le centre liquide fournit à l’étoile une base si solide qu’elle rend un effondrement impossible.
Ces considérations suggèrent deux hypothèses complémentaires :
-
Que l’annihilation de la matière stellaire se produit spontanément, n’étant pas affectée par la température de l’étoile.
-
Que les régions centrales des étoiles ne sont pas dans un état purement gazeux ; leurs atomes, noyaux et électrons sont si serrés qu’ils ne peuvent pas se déplacer librement les uns par rapport aux autres, comme dans un gaz, mais se bousculent plutôt les uns les autres comme les molécules d’un liquide.
Si nous avons eu raison (p. 149) d’attribuer le rayonnement hautement pénétrant observé dans l’atmosphère terrestre à l’annihilation de matière dans des corps astronomiques lointains, alors la première hypothèse est confirmée. Car le rayonnement ne pourrait pas conserver son pouvoir de pénétration élevé observé s’il avait déjà pénétré une grande épaisseur de matière. La difficulté de traverser la matière allonge la longueur d’onde de tous les types de rayonnement (les quanta s’affaiblissent sans cesse), et diminue ainsi son pouvoir de pénétration. Ainsi, quelle que soit l’origine du rayonnement hautement pénétrant, il a dû se propager dans l’espace vide sans trop de difficulté, ce qui revient à dire qu’il a dû provenir d’une matière à une température relativement basse. Ainsi, l’existence d’un rayonnement hautement pénétrant prouve que la matière peut être annihilée en grande quantité à des températures assez basses ; les températures élevées des intérieurs stellaires ne sont pas nécessaires, comme l’affirme la théorie de Russell, pour que l’annihilation se produise.
Un calcul simple montre qu’il ne peut y avoir d’annihilation notable de la substance terrestre. Dans le Soleil, environ un atome sur 1019 est annihilé chaque minute ; si même un dix-millième de ces atomes étaient annihilés sur la Terre, sa surface serait trop chaude pour être habitée. On ne peut plus expliquer cela en disant que le Soleil est chaud et la Terre froide, de sorte que l’annihilation se produit dans le premier cas mais pas dans la seconde. Il faut plutôt supposer que les atomes du Soleil sont d’un type différent de ceux de la Terre. Les atomes solaires s’annihilent spontanément, tandis que les atomes terrestres ne le font pas, ou du moins pas de manière notable.
La seconde de nos hypothèses, selon laquelle les régions centrales des étoiles ressemblent davantage à un liquide qu’à un gaz, est, comme nous l’avons vu, une conséquence nécessaire de la première, mais une preuve indépendante en sa faveur se trouve dans la formation de systèmes binaires par fission. En effet, au chapitre IV (p. 222), nous avons vu qu’une étoile ne pouvait se briser par fission que si elle possédait un centre liquide, ou presque liquide.
[ p. 300 ]
¶ La stabilité des structures stellaires
Pour l’instant, admettons provisoirement l’hypothèse selon laquelle la génération d’énergie stellaire se produit spontanément, comme la désintégration d’atomes radioactifs. Les atomes responsables de la lumière et de la chaleur des étoiles peuvent être considérés comme des atomes superradioactifs qui s’annihilent spontanément et transforment ainsi leur substance en rayonnement.
Nous avons déjà vu que, selon cette conception du mécanisme de génération d’énergie stellaire, une étoile ne peut continuer à briller de manière stable que si ses régions centrales ne sont pas à l’état purement gazeux. Une étoile construite sur des fondations de gaz hautement compressible subit le même sort qu’une maison bâtie sur du sable : elle s’effondre. Une étoile purement gazeuse est une structure dynamiquement instable, et doit se contracter continuellement jusqu’à ce que les atomes de ses régions centrales soient si compacts que leur état ne puisse plus être considéré comme gazeux. Alors, et alors seulement, l’étoile peut exister de manière permanente en tant que structure stable. Ainsi, les régions centrales de toute étoile permanente, le Soleil par exemple, doivent être dans un état que, par souci de concision, nous pouvons qualifier de liquide.
Imaginons maintenant que le Soleil soit dilaté jusqu’à dix fois son diamètre actuel. Sa densité serait alors réduite d’un millième de sa valeur initiale. Le Soleil actuel est 40 % plus dense que l’eau, mais une fois dilaté, il ne serait pas plus dense que l’air atmosphérique ordinaire. Les atomes et les électrons, dix fois plus éloignés, seraient si éloignés les uns des autres que le nouveau Soleil pourrait être considéré comme entièrement gazeux. Il serait donc dynamiquement instable et ne pourrait pas rester dans cet état.
[ p. 301 ] Notre Soleil imaginaire dilaté n’est bien sûr plus une étoile de la séquence principale dans le diagramme de Russell. En dilatant le Soleil à dix fois sa taille actuelle, nous le déplaçons hors de la séquence principale vers une région entièrement vide d’étoiles — en fait, dans le grand gouffre qui se trouve entre les géantes rouges et les naines rouges (voir fig. 22, p. 278). Ainsi, il semble que même si nous plaçons délibérément une étoile dans cette région, elle n’y reste pas, mais se contracte immédiatement jusqu’à ce qu’elle atteigne la séquence principale. Cela ne pourrait-il pas expliquer pourquoi la région en question est inhabitée ?
Imaginons maintenant que le Soleil se contracte à un dixième de son diamètre actuel, de sorte que ses atomes et ses électrons se rapprochent dix fois plus. Sa densité moyenne passe alors de 1,4 à 1 400 fois celle de l’eau, et sa densité centrale d’environ 140 à 140 000. Vous pouvez me contredire en soulignant que si le Soleil est déjà à l’état liquide, il ne peut être comprimé à ce point ; un liquide ne peut généralement pas voir sa densité multipliée par mille. Or, nous avons déjà remarqué que diviser par deux le diamètre d’une étoile double sa température. De même, diviser le diamètre d’une étoile par dix multiplie sa température par dix, de sorte que la température centrale du Soleil passe, par exemple, de 50 millions de degrés à 500 millions de degrés. Et à cette dernière température, les atomes n’existent pratiquement plus en tant que tels ; la matière stellaire est presque entièrement constituée d’électrons et de noyaux libres. Et ces variations sont si infimes que l’augmentation de la densité moyenne du Soleil de 1,4 à 1 400 fois la densité de l’eau est non seulement possible, mais laisse la substance solaire dans un état que l’on pourrait qualifier de gazeux. Une fois de plus, le nouveau Soleil est donc dynamiquement instable. Il serait représenté par un point bien à gauche de la séquence principale, près du milieu de la région inoccupée entre la séquence principale et les naines blanches, mais comme il est instable, il ne peut maintenir sa position ici. Nous voyons à nouveau que même si nous plaçons une étoile dans cette région, elle ne peut y rester. Et, encore une fois, ne se pourrait-il pas que la raison pour laquelle cette région est inoccupée soit qu’elle représente des étoiles instables ?
Une fois de plus, vous pouvez me contredire. Si j’ai bien compris, c’est grâce à l’augmentation de température qui accompagne la contraction. Lorsque nous avons imaginé le Soleil en expansion, n’aurions-nous pas dû prendre en compte la baisse de température qui accompagne cette expansion ? La réponse est oui, mais cela n’aurait rien changé. Une baisse de température entraînera la reformation de plusieurs anneaux L, et peut-être aussi d’anneaux M, d’électrons, de sorte que les nouveaux atomes seront de plus grande taille, mais ils ne perdront pas suffisamment leur liberté de mouvement pour stabiliser le Soleil. Il en aurait été autrement s’il s’était agi d’une étoile dix ou cinquante fois plus lourde que le Soleil ; on pourrait alors démontrer que la reformation des anneaux K et L aurait produit une série de configurations stables. Et la branche d’éperon du diagramme de Russell existe précisément pour abriter de telles étoiles.
Le problème dans son ensemble est trop complexe pour être abordé de manière satisfaisante de manière fragmentaire ; une analyse mathématique approfondie implique une analyse mathématique très complexe. Cette analyse montre que le diagramme de Russell peut être divisé en régions représentant des configurations stables et instables, comme illustré dans la fig. 24.
Les zones instables sont ainsi marquées ; les zones restantes sont stables. Les points qui forment une sorte d’arrière-plan [ p. 303 ] du diagramme représentent 2 100 étoiles dont les magnitudes absolues sont connues grâce à leurs parallaxes déterminées spectroscopiquement au Mont Wilson. Le matériel d’observation n’est pas parfait, car une incertitude considérable s’attache à toutes les parallaxes spectroscopiques des étoiles de type B, et les étoiles de type A sont presque non représentées car il est pratiquement impossible d’obtenir leurs parallaxes par la méthode spectroscopique [ p. 303 ]. Les courbes théoriques sont probablement encore plus imparfaites, mais, telles qu’elles sont, elles semblent suggérer très fortement que les régions occupées et inoccupées coïncident avec celles représentant des configurations stables et instables ; après avoir pris en compte toutes les imperfections possibles de la théorie et de l’observation, il reste encore trop de concordance à expliquer comme une simple coïncidence.
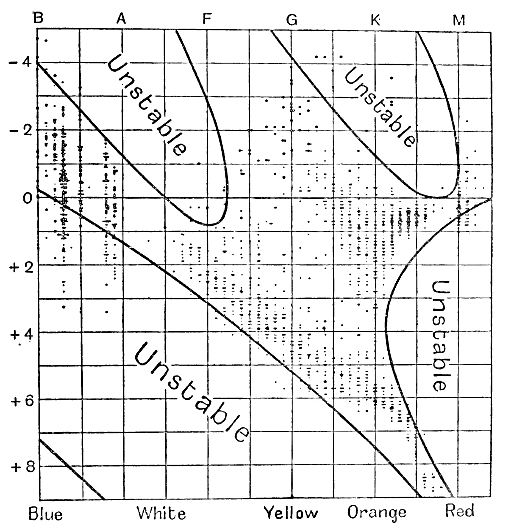
Ainsi, la conclusion à laquelle semble conduire la discussion mathématique est que les régions occupées du diagramme de Russell représentent des étoiles dont les régions centrales sont à l’état liquide, ou presque liquide. Toutes les autres étoiles sont instables, de sorte que les régions correspondantes du diagramme de Russell sont nécessairement vacantes. En termes plus techniques, toutes les étoiles du ciel doivent avoir un centre liquide, ou presque liquide.
Nous avons ici une pièce du puzzle qui semble correspondre à celle découverte au Chapitre IV, où nous avons découvert qu’une étoile ne pouvait se briser par fission que si elle possédait un centre liquide, ou presque liquide. Les preuves s’accumulent que les étoiles ont des centres liquides plutôt que gazeux.
Les critiques de l’hypothèse précédente — généralement décrite comme l’hypothèse de « l’étoile liquide » — ont principalement porté sur le fait que les diamètres des anneaux atomiques K sont si petits que les atomes des anneaux K dans les régions centrales du Soleil ne peuvent être suffisamment serrés pour entraîner un écart substantiel par rapport à l’état gazeux. Il est difficile de discuter, et encore plus de répondre, à cette critique sans connaître les diamètres précis de ces atomes des anneaux K. Nous connaissons bien sûr les diamètres attribués à l’anneau K par la théorie de Bohr (p. 129), mais personne ne soutient plus que cette théorie donne une image fidèle de l’atome. Elle fournit [ p. 305 ] est un bon modèle de travail dans certaines limites, mais nous ne savons pas où s’arrêtent ces limites. La seule expérience pratique que nous ayons des atomes du cycle K concerne les atomes d’hélium ; la théorie de Bohr leur attribue un diamètre de 0,54 x 10-8 cm. Pourtant, l’hélium solide et liquide fournit une illustration pratique de la proximité avec laquelle les atomes d’hélium peuvent être entassés ; dans ceux-ci, chaque atome occupe une sphère de diamètre 4 x 10-8 cm, soit plus de 400 fois l’espace qui lui est alloué par la théorie de Bohr. Il semble que nous soyons encore loin d’une connaissance précise des dimensions des cycles K d’électrons.
La nouvelle mécanique ondulatoire de Schrödinger dresse un tableau très différent des intérieurs atomiques de la théorie plus simple de Bohr, qu’elle supplante rapidement. Même l’électron diffère considérablement de l’électron de l’ancienne théorie de Bohr. Il n’est l’électron d’antan que lorsqu’il se trouve à une distance infinie du noyau. À mesure qu’il se rapproche progressivement de ce noyau, il subit une métamorphose d’un type que personne n’a encore réussi à décrire, et il est totalement impossible de dire quelle forme il a pu prendre au moment où il accomplit ce que nous appelons « décrire une orbite en anneau K ». Tout ce que nous savons de l’orbite en anneau K est son énergie, et il semble impossible de prédire l’espace occupé par une telle orbite tant que nous n’aurons pas une meilleure connaissance des qualités de l’article qui la décrit.
Il faut bien sûr admettre que les preuves physiques, telles qu’elles existent, semblent indiquer que les atomes du cycle K sont sensiblement plus petits que ce qui est nécessaire pour l’hypothèse de l’étoile liquide. Mais les preuves astronomiques me semblent plus solides et plus fiables, et pointent exactement dans la direction opposée. Et là, nous devons laisser l’énigme de côté jusqu’à ce que de nouvelles pièces soient découvertes.
[ p. 306 ] Tant que nous ne connaissons pas le type d’atomes qui composent une étoile particulière, nous ne pouvons pas calculer dans quelle mesure ils seront fragmentés par la température interne de l’étoile. Par conséquent, les courbes théoriques de démarcation entre configurations stables et instables ne peuvent être calculées sans supposer des numéros atomiques définis pour les atomes stellaires.
Les courbes présentées dans la fig. 24 ont été tracées pour un numéro atomique d’environ 95, légèrement supérieur à celui de l’uranium (92). Ce numéro atomique a été choisi car il s’est avéré offrir la meilleure concordance entre théorie et observation, mais nous verrons que d’autres considérations justifient notre choix.
¶ Structure stellaire
Une étoile, comme une maison ou un tas de sable, est une structure qui s’effondrerait sous son propre poids si chaque couche n’était pas maintenue contre la gravité par la pression exercée par la couche interne suivante. Cette pression n’est pas, comme la pression ordinaire d’un gaz, le résultat de l’impact de molécules entières. Elle est produite en partie par l’impact d’un certain nombre d’atomes dépouillés de leurs électrons presque entièrement, voire jusqu’à leur noyau, mais dans une bien plus grande mesure par l’impact d’une pluie d’électrons libres. Dans les étoiles massives, une pression supplémentaire est produite par l’impact du rayonnement qui, comme nous l’avons vu, emporte un poids et exerce ainsi une pression sur tout obstacle rencontré. Les impacts combinés des électrons libres, des atomes (ou noyaux nus) et du rayonnement empêchent l’étoile de s’effondrer sous sa propre attraction gravitationnelle.
[ p. 307 ] Ceci donne une image instantanée assez bonne de la structure d’une étoile. L’image correspondante de son mécanisme est obtenue en considérant les noyaux comme des particules de rayons α, les électrons libres comme des particules de rayons β et le rayonnement comme des rayons γ (bien que dans la plupart des étoiles, la majeure partie du rayonnement ait la longueur d’onde des rayons X). Tous ces rayons se frayent un chemin à travers l’étoile et, exactement comme dans les travaux de laboratoire, les rayons β sont plus pénétrants que les rayons α, et les rayons γ sont plus pénétrants que les deux.
Le transport d’énergie dans une étoile. Nous avons vu que la chaleur d’un gaz n’est que l’énergie de son mouvement moléculaire. La conduction de la chaleur dans un gaz est généralement étudiée en considérant chaque molécule comme un vecteur d’énergie ; lorsqu’elle entre en collision avec une seconde molécule, l’énergie des deux molécules en collision est redistribuée entre elles, et ainsi la chaleur est transportée des régions les plus chaudes vers les régions les plus froides. Chaque molécule possède une puissance de transport proportionnelle à son énergie de mouvement, à sa vitesse et à son « libre parcours » – la distance parcourue entre deux collisions successives.
À l’intérieur d’une étoile, trois types distincts de porteurs sont en action : les atomes (ou noyaux nus), les électrons libres et le rayonnement. On peut comparer leurs capacités relatives de porteurs en multipliant l’énergie, la vitesse et le libre parcours de chacun. À cette fin, le « libre parcours » du rayonnement peut être considéré comme la distance parcourue par le rayonnement avant d’être absorbé à 37 %, puisqu’il s’agit de la distance moyenne parcourue par son énergie. Le calcul révèle que la capacité de transport des noyaux et des électrons est insignifiante comparée à celle du rayonnement. Les noyaux [ p. 308 ] et les électrons ont peut-être la plus grande quantité d’énergie à transporter, mais en raison de leur plus faible pouvoir de pénétration, la distance sur laquelle ils la transportent, leur libre parcours, est bien inférieure à celle du rayonnement. Leur vitesse de transport est également plus faible, car le rayonnement transporte son énergie à la vitesse de la lumière. Ainsi, la quasi-totalité du transport d’énergie de l’intérieur d’une étoile vers sa surface s’effectue par rayonnement.
Ce principe général fut clairement énoncé pour la première fois par Sampson en 1894. Il démontra également comment la température de tout petit fragment de l’intérieur d’une étoile doit être déterminée par la condition que celui-ci reçoive autant de rayonnement qu’il en émet. Cependant, ses applications détaillées furent faussées par l’utilisation d’une loi erronée du rayonnement. Douze ans plus tard, Schwarzschild avança indépendamment la même idée et l’exprima dans les équations mathématiques d’« équilibre radiatif », qui ont servi de base à toutes les discussions ultérieures sur le problème.
Du fait que le rayonnement surpasse complètement les atomes et les électrons pour transporter l’énergie de l’intérieur d’une étoile vers sa surface, il s’ensuit que la structure d’une étoile doit être déterminée par l’opacité de la matière qu’elle contient. Si celle-ci est altérée, la capacité de transport du rayonnement est modifiée, ce qui affecte toute la structure de l’étoile. Une étoile dont l’intérieur serait entièrement transparent ne pourrait retenir aucune chaleur ; tout son intérieur serait à très basse température et l’étoile serait immense. En revanche, dans une étoile très opaque, toute l’énergie resterait accumulée à l’endroit où elle a été générée, de sorte que la température intérieure deviendrait très élevée et le diamètre de l’étoile serait [ p. 309 ] proportionnellement petit. Ce sont bien sûr les cas intermédiaires qui présentent un intérêt pratique, mais les cas extrêmes que nous venons de mentionner montrent comment la structure d’une étoile dépend de son opacité.
Malheureusement, il est impossible d’obtenir une mesure directe de l’opacité de la matière stellaire. Nous ne pouvons même pas mesurer l’opacité de la matière terrestre dans des conditions stellaires, car l’intérieur des étoiles est à des températures incomparablement plus élevées que celles disponibles en laboratoire. Cependant, nous savons que l’opacité de la matière stellaire est due aux atomes, aux noyaux et aux électrons libres qui la composent, qui contrôlent le trajet du rayonnement. Bien que nous ne puissions obtenir un échantillon de matière stellaire, nous savons avec une assez grande certitude combien d’atomes, de noyaux et d’électrons un tel échantillon contiendrait. Déterminer son opacité relève donc du calcul théorique.
Un tel calcul fut effectué par le Dr Kramers de Copenhague en 1923, et ses résultats furent généralement acceptés. Plus récemment, M. Gaunt de Cambridge a effectué un calcul beaucoup plus précis et obtenu des résultats très proches de ceux initialement avancés par Kramers. Dans la mesure où ces résultats peuvent être testés en laboratoire, ils concordent parfaitement avec l’observation. Et, bien qu’il existe un écart important entre les conditions de laboratoire et les conditions stellaires, il est difficile d’imaginer comment la formule de Kramers pourrait échouer dans les étoiles.
À partir de cette formule, nous pouvons déterminer complètement la structure des étoiles, ou, si la structure de l’étoile est supposée être connue, la formule de Kramers nous indique le taux auquel l’énergie circule vers sa surface (cela dépend entièrement de l’opacité de la substance de l’étoile), et cela nous indique à son tour à quel taux l’énergie doit être générée à l’intérieur de l’étoile pour qu’elle puisse rester [ p. 310 ] en équilibre dans la configuration en question. Comme on pouvait s’y attendre, des configurations de diamètres différents nécessitent des taux de génération d’énergie différents. Dans la nature, une étoile doit ajuster son diamètre pour s’adapter au taux auquel elle génère de l’énergie ; ce faisant, elle fixe non seulement son diamètre, mais aussi sa température de surface, sa couleur et son type spectral. Si le taux de génération d’énergie d’une étoile devait changer soudainement, l’étoile se dilaterait ou se contracterait jusqu’à atteindre le rayon et la température adaptés à son nouveau taux de génération d’énergie.
Français Des calculs détaillés montrent que, pour les étoiles entièrement gazeuses, de grands diamètres correspondent à une faible génération d’énergie et vice versa. Ainsi, si les étoiles étaient entièrement gazeuses, les géantes rouges seraient moins lumineuses que les étoiles de la séquence principale de même masse. Le diagramme de Seares, reproduit à la p. 282, montre que l’inverse est en fait le cas, une géante rouge émettant de 10 à 20 fois plus de rayonnement total qu’une étoile de la séquence principale de même masse. Cela fournit une preuve contre le fait que les étoiles soient entièrement gazeuses, mais il existe des preuves plus solides que cela. Pour les étoiles entièrement gazeuses, les lignes épaisses représentées sur le diagramme de Seares seraient des lignes droites obliques, inclinées vers le haut à gauche. La grande divergence entre un tel système de lignes obliques et les courbes représentées dans la fig. 23 donne une indication de la mesure dans laquelle l’état de la matière stellaire diverge de l’état purement gazeux.
Selon la théorie de Kramers, l’opacité de la matière dépend du numéro atomique et du poids atomique des atomes qui la composent. Un gros caillot de matière, sous la forme d’un noyau atomique massif, absorbe bien plus efficacement les radiations qu’un grand nombre de petits caillots de même poids total. L’expérience terrestre quotidienne le démontre. C’est pour cette raison que le physicien et le chirurgien choisissent tous deux le plomb comme matériau de blindage de leur appareil à rayons X ; ils constatent qu’une tonne de plomb est bien plus efficace pour arrêter les rayons X indésirables qu’une tonne de bois ou de fer. Si nous connaissions la résistance d’un appareil à rayons X et le poids total du matériau de blindage qui l’entoure, nous pourrions estimer très précisément le poids atomique de ce matériau en mesurant la quantité de rayonnement X qui s’en échappe.
Une méthode très similaire peut être utilisée pour déterminer la masse atomique des atomes qui composent les étoiles. Une étoile n’est en réalité qu’un immense appareil à rayons X. Nous connaissons la masse de nombreuses étoiles, et la vitesse à laquelle elles génèrent des rayons X n’est autre que la vitesse à laquelle elles rayonnent de l’énergie dans l’espace. Si nous pouvions couper chaque noyau atomique d’une étoile en deux, nous diviserions par deux l’opacité de l’étoile, de sorte que le rayonnement traverserait deux fois plus loin avant d’être absorbé. Si l’étoile était entièrement gazeuse, son expansion quadruplerait son diamètre initial et sa température de surface serait divisée par deux. Il s’ensuit que nous pouvons calculer la masse atomique des atomes qui composent une étoile à partir de sa masse, de sa luminosité et de sa température de surface.
Les poids atomiques d’un certain nombre d’étoiles, que j’ai calculés en supposant qu’elles étaient entièrement gazeuses, se sont révélés dans presque tous les cas supérieurs à celui de l’uranium, l’atome le plus lourd connu sur Terre. Ils se sont avérés non seulement plus élevés, mais énormément plus élevés ; si élevés en effet qu’ils paraissent totalement improbables. Là encore, l’explication semble être que les étoiles ne sont pas entièrement gazeuses. Dès que l’on suppose que l’intérieur des étoiles est partiellement liquide, les poids atomiques calculés diminuent considérablement. Ils ne peuvent plus être déterminés avec exactitude, mais le numéro atomique d’environ 95 auquel nous avons été conduits en examinant le diagramme de Russell semble parfaitement cohérent avec tous les faits connus.
En effet, d’autres considérations semblent suggérer que les numéros atomiques des atomes stellaires doivent être supérieurs à 92. A priori, le rayonnement stellaire pourrait provenir soit de types de matière connus de nous sur Terre, soit d’autres types inconnus. Une fois admis que la température et la densité élevées ne peuvent rien faire pour accélérer la génération de rayonnement par la matière ordinaire, il devient clair que le rayonnement stellaire ne peut provenir de types de matière connus de nous sur Terre. D’autres types de matière doivent exister, et comme, à deux exceptions près, tous les numéros atomiques jusqu’à 92 (uranium) sont déjà occupés par des éléments terrestres, il semble probable que ces autres types doivent être des éléments de masse atomique supérieure à celle de l’uranium.
Il ne faut pas s’attendre à ce que ces atomes superlourds révèlent leur présence dans les spectres stellaires, car ceux-ci ne nous renseignent que sur la constitution de l’atmosphère des étoiles. Et comme les atomes les plus légers flottent à la surface, ce sont eux, en majorité, qui figurent dans les spectres stellaires. Si l’atmosphère solaire avait contenu un nombre considérable d’atomes superlourds à la naissance des planètes, certains d’entre eux devraient encore exister sur Terre. Il ne peut y en avoir un grand nombre, sinon leur forte production d’énergie les trahirait. L’hypothèse la plus simple semble être que les atomes les plus lourds descendent au centre des étoiles et que la Terre s’est formée principalement, voire uniquement, à partir des atomes plus légers qui ont flotté à la surface du Soleil.
¶ Évolution stellaire
Nous avons supposé que les étoiles étaient initialement nées sous forme de condensations aux franges externes des nébuleuses spirales. De par leur mode de formation, ces condensations seraient nécessairement de tailles diverses, et soumises à la seule restriction qu’aucune d’entre elles ne puisse être inférieure à une certaine limite de masse. On ne peut donc pas s’attendre à ce que les étoiles, à leur naissance ou ultérieurement, soient toutes de même taille ou de même masse, ni toutes dans les mêmes conditions physiques. Les étoiles débuteraient leur existence à différents points du diagramme de Russell, mais on peut imaginer que leurs positions initiales se limitent aux parties du diagramme susceptibles d’être occupées par des étoiles – soit, comme le suggère l’hypothèse des étoiles liquides, parce que ce sont les seules configurations stables, soit pour une autre raison encore inconnue. Chaque année, une étoile perd une certaine masse, et son taux de production d’énergie, et donc sa luminosité, diminuent d’autant, ce qui la fait changer de position sur le diagramme. Reprenons le diagramme de Seares sur les masses stellaires [p. [282] (#p282), on peut considérer les courbes de même poids comme une série de marches – des marches très inégales, il est vrai – chacune représentant un poids inférieur à celui du dessus. Quelle que soit l’évolution d’une étoile, il est essentiel qu’elle descende toujours les marches : toute montée est impossible.
Dans le diagramme de Russell, nous pouvons tracer deux voies possibles d’évolution stellaire, qui n’impliquent aucune entrée dans des régions inoccupées par les étoiles – deux voies que l’armée stellaire peut emprunter pour transformer sa substance en rayonnement. La première est bien sûr la « séquence principale », que de nombreuses considérations suggèrent comme étant la ligne de marche principale de l’armée stellaire. La branche qui part des géantes rouges dans le diagramme de Russell représente une seconde ligne de marche possible : un certain nombre d’étoiles parcourent cette branche jusqu’à atteindre la séquence principale sous forme d’étoiles bleues ou blanches, puis descendent dans la moitié inférieure de la séquence principale pour finir sous forme d’étoiles rouges de faible luminosité, passant à l’extinction finale.
La progression sur chacune de ces voies s’accompagne d’une diminution continue de la taille de l’étoile, son diamètre diminuant régulièrement. Cela ne signifie pas que la densité de l’étoile augmente continuellement, car son poids diminue continuellement, de sorte que même si sa densité restait la même, son diamètre diminuerait. Néanmoins, une étude des densités moyennes déterminées par Seares, comme le montre le diagramme de la p. 282, suggère une augmentation continue de la densité, bien que celle-ci devienne très faible au milieu de la séquence principale.
Pratiquement toutes les théories de l’évolution stellaire qui ont jamais été proposées ont imaginé que l’inarche de l’armée stellaire était du même type général que celle qui vient d’être décrite, bien que l’opinion actuelle soit peut-être encline à considérer la séquence principale comme la principale ligne de marche, alors que les théories antérieures supposaient que les étoiles les plus jeunes suivaient uniquement la branche des géantes rouges, ne rejoignant la séquence principale qu’à l’âge mûr. La première théorie sérieuse, celle de Lockyer, était exprimée en termes de branches de température ascendante et descendante, formant ensemble cette dernière ligne de marche dans le diagramme de Russell. Une théorie proposée par Russell en 1913 attribuait à nouveau aux étoiles les lignes de marche qui viennent d’être décrites. Elle tentait également une explication physique, abandonnée depuis, expliquant pourquoi les étoiles suivaient ces trajectoires particulières plutôt que d’autres. Sa théorie la plus récente de 1925 ne différait de sa théorie antérieure qu’en donnant la nouvelle explication, que nous avons déjà discutée (p. 293), quant à la raison pour laquelle les étoiles suivaient ces chemins particuliers.
À l’heure actuelle, on peut probablement affirmer que la quasi-totalité des astronomes s’accordent sur le fait que les trajectoires évolutives des étoiles correspondent au type général que nous avons décrit. Certaines étoiles sont initialement des géantes rouges, d’autres des étoiles bleues, d’autres encore des étoiles intermédiaires. En vieillissant, elles descendent toutes dans le diagramme de Russell, leurs trajectoires convergeant vers un point situé à la fourche de la γ inversée, représentée sur la [fig. 22] (#Universe_figure_22), et après avoir dépassé ce point, elles descendent dans la séquence principale. En revanche, les opinions divergent largement quant à l’interprétation physique de ces trajectoires. La plupart des astronomes suspendent probablement leur jugement en attendant des observations précises permettant de trancher entre des théories contradictoires.
Lorsque les étoiles sont apparues sous forme de particules de brouillard ardent projetées par des nébuleuses en rotation, elles étaient constituées de mélanges d’atomes de toutes sortes, certains ayant peut-être une durée de vie si courte qu’ils se transformaient presque instantanément en rayonnement, et d’autres ayant une durée de vie si longue qu’on peut les qualifier de permanents. À l’exception d’un petit nombre d’atomes radioactifs, la Terre doit être entièrement constituée d’atomes de ce dernier type. Les calculs montrent que les atomes terrestres doivent avoir une durée de vie considérablement plus longue que l’atome stellaire moyen, sinon leur auto-annihilation rendrait la Terre trop chaude pour être habitée. Les atomes permanents d’une étoile ne contribuent pratiquement pas à sa capacité de production d’énergie et ne font donc qu’augmenter son poids. Les atomes à la durée de vie la plus courte contribuent grandement à la production d’énergie de l’étoile tout en ajoutant peu à son poids. En général, plus la durée de vie d’un atome est courte, plus la proportion de ses nombres annihilés par an est grande, et donc plus la quantité d’énergie qu’il génère par tonne de poids est grande.
Une étoile commence sa vie avec une forte proportion d’atomes à courte durée de vie, et génère donc d’abord énormément d’énergie. En vieillissant, les atomes les plus éphémères disparaissent en premier, réduisant ainsi la production moyenne d’énergie par tonne de l’étoile. Ainsi, à mesure que le poids de l’étoile diminue, son taux de production d’énergie par tonne doit également diminuer. Finalement, tous les atomes ayant une grande capacité de production d’énergie ont disparu, et l’étoile se retrouve réduite à une masse d’atomes réduite et diminuée, dont la capacité de rayonnement est très faible.
Autrement dit, le taux de production d’énergie par tonne d’une étoile est proportionnel au taux de mortalité de sa population atomique. Dire que Sirius produit 16 fois plus d’énergie par tonne que le Soleil revient à dire que l’atome moyen de Sirius n’a qu’un seizième de l’espérance de vie des atomes solaires ; leur taux de mortalité est 16 fois plus élevé. À mesure que les atomes les plus mortels disparaissent progressivement dans une étoile, le taux de mortalité moyen de la population diminue, ou, en d’autres termes, à mesure qu’une étoile vieillit, sa capacité de production d’énergie par tonne diminue.
Cela concorde avec les résultats de l’astronomie observationnelle. Les étoiles les plus massives génèrent non seulement plus d’énergie que les étoiles moins massives, comme on pouvait s’y attendre, mais elles produisent aussi énormément plus d’énergie par tonne. Ceci est illustré par la liste suivante d’étoiles de la séquence principale :
[ p. 317 ]
| Étoile | Poids (en termes de soleil) | Production d’énergie (ergs par gramme) |
|---|---|---|
| Étoile de Pearce A | 36,3 | 15 000 |
| V Puppis A | 19,2 | 1 000 |
| Sirius A | 2.45 | 29 |
| Soleil | 100 | 1,90 |
| ε Éridani | (0,45) | 0,26 |
| Kruger 60 B | 0,20 | 0,021 |
Le diagramme des poids stellaires de Seares ([#p282]) montre qu’il s’agit d’une propriété générale des étoiles. Pour reprendre notre métaphore précédente, les étoiles gaspillent généreusement leur substance dans leur jeunesse, alors qu’il leur en reste largement, mais la parcimonie les gagne avec l’âge. Des considérations théoriques nous ont maintenant permis d’expliquer ce phénomène.
Le même diagramme montre que deux étoiles de même masse n’ont généralement pas la même luminosité. En général, les étoiles géantes de la branche de l’éperon menant aux géantes rouges ont des luminosités nettement supérieures à celles des étoiles de la séquence principale de même masse. Nous avons déjà remarqué qu’une géante rouge peut émettre jusqu’à 10 ou 20 fois le rayonnement d’une étoile de même masse de la séquence principale. Le même phénomène se reproduit lorsque l’on passe des étoiles de la séquence principale aux naines blanches. Les étoiles de la séquence principale émettent un rayonnement considérablement plus important – jusqu’à 500 fois plus – que les naines blanches de même masse. Ceci est illustré par les trois naines blanches suivantes, que l’on peut comparer aux trois dernières étoiles du tableau précédent :
| Étoile | Poids (en termes de soleil) | Production d’énergie (ergs par gramme) |
|---|---|---|
| Sirius B | 0,85 | 0,0027 |
| ο2 Éridani B | 0,44 | 0,002 |
| l’étoile de van Maanen | (0,20) | (0,00055) |
[ p. 318 ] Nous avons jusqu’ici supposé que la génération d’énergie était spontanée et donc insensible aux changements des conditions physiques. Pourtant, les faits qui viennent d’être mentionnés semblent suggérer que cela ne peut guère être toute la vérité. Pour formuler l’objection en termes d’un exemple concret, Sirius A et sa compagne naine blanche Sirius B doivent selon toute probabilité être nées en même temps, dans la même nébuleuse (p. 284), alors que la première génère 4 000 fois plus d’énergie par tonne que la seconde. Il semble improbable qu’une telle différence puisse être attribuée à différents types d’atomes ; l’origine commune des deux étoiles l’exclut presque totalement. Nous savons que les atomes sont dans des conditions physiques différentes dans les deux étoiles ; Dans Sirius A, ils ont conservé leurs anneaux K intacts, tandis que dans Sirius B, la naine blanche, ils sont complètement décomposés en noyaux nus et en électrons libres. Si les deux composants de Sirius sont constitués essentiellement des mêmes types d’atomes, comme leur origine commune le laisse supposer, alors l’énorme différence dans les taux de production d’énergie de ces atomes semble dépendre des conditions physiques différentes de leurs atomes.
Les considérations avancées au Chapitre III rendent hautement probable que le taux de génération d’énergie d’une étoile dépende de l’état physique de ses atomes. Nous y supposions que l’énergie stellaire était générée par la coalescence d’électrons avec des protons ; les protons n’existent que dans les noyaux atomiques, et des considérations purement physiques ont conduit à la conjecture que les seuls électrons capables de coalescer avec un proton particulier sont ceux qui décrivent momentanément des orbites autour du noyau dans lequel réside le proton. L’étude de la structure stellaire appuie cette hypothèse, car si l’énergie pouvait être générée par des électrons libres tombant [ p. 319 ] dans les noyaux, on pourrait démontrer que l’étoile entière serait instable et exploserait dans un éclair de rayonnement. Selon cette hypothèse, une étoile dont seuls quelques atomes possèdent encore des électrons en mouvement orbital ne peut évidemment générer que peu d’énergie. Ceci explique à la fois la faible capacité énergétique des naines blanches et permet de comprendre pourquoi les géantes rouges, où subsistent les anneaux d’électrons L et M, génèrent plus d’énergie que les étoiles de la séquence principale de même masse.
À mesure qu’une étoile vieillit et que son poids diminue, elle doit continuellement adopter de nouvelles configurations, par exemple pour que son émission d’énergie soit égale à son taux interne de production d’énergie. Une même étoile peut être tour à tour une géante rouge, une étoile de la séquence principale et une naine blanche. En d’autres termes, une étoile ajuste continuellement son diamètre en fonction de son taux de production d’énergie.
Dans l’hypothèse que nous venons de considérer, une étoile modifie à la fois son émission et sa production d’énergie en changeant de diamètre. À chaque instant, elle doit choisir un diamètre pour lequel les deux s’équilibrent parfaitement. L’étoile possède une gamme si large de taux de production, selon qu’il lui reste peu ou beaucoup d’électrons en mouvement orbital, qu’elle est susceptible de toujours trouver une configuration d’équilibre. En tout cas, toutes les étoiles du ciel semblent l’avoir fait, à l’exception des étoiles à longue période qui sont en expansion et en contraction constantes, comme si elles ne parvenaient pas à trouver un diamètre pour lequel leurs apports et leurs dépenses d’énergie s’équilibreraient.
Cette même hypothèse permet immédiatement de conclure que la grande variété d’étoiles du système galactique a approximativement le même âge et qu’elles sont donc toutes nées de la même nébuleuse. Les étoiles galactiques les plus lumineuses peuvent difficilement avoir généré de l’énergie à leur rythme actuel pendant plus de 100 000 millions d’années environ ; un âge plus long nécessiterait un poids initial incroyablement élevé. Pourtant, les mouvements des étoiles indiquent que même ces étoiles très lumineuses doivent exister depuis au moins 50 fois cette période. Cette apparente contradiction disparaît si l’on admet que l’extrême luminosité des étoiles les plus brillantes pourrait être un développement récent et que, pendant peut-être 98 % de sa vie, une telle étoile n’a perdu que peu d’énergie, car la plupart de ses atomes étaient dépourvus d’électrons et étaient donc à l’abri de l’annihilation. La proportion requise de 98 pour cent peut paraître étrangement élevée, mais nous avons énoncé un cas extrême ; nous n’avons besoin d’exiger une proportion aussi grande que dans le cas d’un type d’étoile très rare : probablement pas plus d’une étoile sur dix millions est d’un tel type.
Dans leur état de dormance antérieur, ces étoiles, aujourd’hui si lumineuses, auraient été en réalité des naines blanches d’une masse énorme. L’astronomie observationnelle ne fournit aucune preuve de l’existence de telles étoiles, mais rien ne prouve non plus leur inexistence. Les étoiles très massives sont connues pour être des objets très rares, de sorte qu’il faudrait probablement parcourir une longue distance du Soleil avant d’en trouver une, et elle pourrait alors être si éloignée qu’elle serait invisible depuis la Terre. Quoi qu’il en soit, une étoile très lointaine et de faible luminosité aurait de fortes chances d’échapper à la détection. On ne peut pas déduire l’inexistence de telles étoiles du fait qu’aucune n’a encore été découverte.
De plus, il est loin d’être absolument certain que de telles étoiles n’aient pas été découvertes. Les naines blanches très massives [ p. 321 ] devraient avoir des températures de surface plus élevées que les étoiles massives de la séquence principale ou que les naines blanches connues, qui sont toutes de faible masse. On connaît tout un groupe d’étoiles — les étoiles de type O — dont les spectres indiquent en effet des températures très élevées. On les interprète généralement comme des étoiles d’une luminosité énorme à des distances énormes, mais il est possible que certaines d’entre elles au moins soient des étoiles de faible luminosité à des distances modérées. En particulier, les étoiles centrales des nébuleuses planétaires sont de types O et B. Mais alors que l’étoile normale de la séquence principale de ces types spectraux est généralement environ mille fois plus lumineuse que le Soleil, les étoiles centrales des nébuleuses planétaires se révèlent être considérablement moins lumineuses que le Soleil. Le Dr Gerasimovic a récemment démontré que 52 de ces étoiles ont une luminosité moyenne équivalant seulement aux deux tiers environ de celle du Soleil. D’autres observateurs ont trouvé des luminosités encore plus faibles. Comme la température de surface de ces étoiles doit être de l’ordre de 30 000 degrés, elles doivent être minuscules ; un simple calcul montre même qu’elles ne peuvent guère dépasser un dixième du rayon du Soleil.
Non seulement elles sont de petite taille, mais certains indices suggèrent qu’elles sont d’un poids important. Des données spectroscopiques montrent que, dans de nombreux cas, les nébuleuses environnantes sont en rotation et, tout comme pour la galaxie (p. 69) et les immenses nébuleuses extragalactiques (p. 71), leur poids peut être calculé à partir de leurs vitesses de rotation observées. Celles-ci semblent indiquer des poids moyens d’environ 40 à 50 fois le poids du Soleil. Campbell et Moore, de l’observatoire Lick, ont calculé que la nébuleuse planétaire NGC 7009 devait avoir 162 fois le poids du Soleil, mais de nombreux facteurs se combinent pour rendre cette estimation plutôt incertaine.
[ p. 322 ] Tout ceci suggère que les étoiles centrales des nébuleuses planétaires doivent, selon toute probabilité, être considérées comme des « naines blanches » d’un poids énorme. Il semble possible qu’elles soient exactement le type d’étoiles requis par notre théorie. Les 52 nébuleuses planétaires déjà mentionnées ont la même distance moyenne au Soleil et la même distribution par rapport à la galaxie que les étoiles de type O, de sorte qu’il est possible que les étoiles de type O et les nébuleuses planétaires soient des formes adoptées successivement ou alternativement au cours de l’évolution de corps similaires. Il convient de mentionner que les nébuleuses planétaires présentent des déplacements spectraux qui, s’ils étaient interprétés de manière ordinaire, indiqueraient qu’elles se déplacent à des vitesses très élevées, atteignant dans certains cas des centaines de kilomètres par seconde. De telles vitesses seraient totalement inappropriées pour des étoiles de poids important. Pourtant, cette objection est plutôt dénuée de fondement, car si les décalages spectraux provenaient réellement de vitesses de mouvement élevées, la plus élevée des vitesses observées suffirait à éloigner complètement du système galactique les nébuleuses planétaires qui les possèdent ; elles seraient des voyageuses aléatoires à travers notre système stellaire, alors que leur disposition ordonnée et leur concentration près du plan galactique suggèrent très fortement qu’elles en sont des membres permanents. Ainsi, les grands décalages observés des raies spectrales peuvent difficilement indiquer de grandes vitesses dans l’espace ; une autre interprétation doit être trouvée. Le professeur Perrine considère qu’ils proviennent principalement des mouvements internes, contraction, expansion et rotation des nébuleuses. Si tel est le cas, les mouvements dans l’espace ne peuvent être déterminés, mais au moins ils ne présentent plus de difficulté. Si ces étoiles sont, comme le requiert notre hypothèse, des naines blanches de très grande masse et de petit rayon, leurs spectres devraient [ p. 323 ] pour présenter un déplacement de relativité vers le rouge du même type que celui observé réellement dans Sirius B. Il est possible que cela présente une difficulté plus sérieuse, bien qu’il soit également possible qu’il se révèle à nouveau fusionné dans les grands déplacements observés.
Au vu de tout cela, il semble tout à fait possible que les nébuleuses planétaires, ainsi que d’autres étoiles de type O ou B de faible luminosité, soient des étoiles très massives dans l’état dormant envisagé par l’hypothèse que nous venons d’évoquer. En bref, nous imaginons qu’une étoile massive puisse conserver son poids en existant sous forme de nébuleuse planétaire ou d’étoile naine de type O pendant des millions de millions d’années, puis surgir sous forme d’étoile hautement lumineuse avec toute l’apparence d’une jeunesse extrême. Mais les preuves observationnelles sont actuellement insuffisantes, que ce soit pour ou contre une telle hypothèse. Certaines pièces du puzzle manquent, et nous ne pouvons qu’attendre qu’elles apparaissent.
Naines blanches. Hormis ces hypothétiques naines blanches massives, les astronomes considèrent généralement les naines blanches ordinaires comme le stade final de l’évolution stellaire. Il est généralement admis qu’il s’agit d’étoiles dont la température centrale est si élevée que leurs atomes sont dépourvus d’électrons, mais il n’existe pas de consensus sur les raisons pour lesquelles les étoiles rétrécissent jusqu’à cet état.
Selon l’hypothèse de l’étoile liquide, les régions inoccupées du diagramme de Russell représentent des configurations instables. Habituellement, une légère perte de poids d’une étoile la déplace simplement vers une nouvelle position dans le diagramme, contiguë à l’ancienne. Il arrive cependant que ce léger déplacement entraîne l’étoile dans une région instable du diagramme, auquel cas elle traversera précipitamment cette région, jusqu’à aboutir finalement à une configuration stable totalement différente.
L’hypothèse de l’étoile liquide explique l’état de naine blanche tout simplement comme l’état final vers lequel une étoile se contracte de manière cataclysmique lorsque sa production d’énergie n’est plus suffisante pour lui permettre de figurer dans la séquence principale. Dans cet état, l’étoile rayonne si peu d’énergie que l’annihilation et la désintégration sont presque entièrement arrêtées. Nous avons vu que si le Soleil continuait à rayonner à son rythme actuel pendant 15 millions de millions d’années, tout son poids serait transformé en rayonnement. En revanche, l’étoile de van Maanen peut, et continuera probablement à rayonner à son rythme actuel pendant 15 millions de millions d’années sans perdre plus d’environ un millième de son poids actuel. On peut considérer l’état de naine blanche comme un état final où les changements et la désintégration ont si pratiquement disparu qu’une étoile qui se contracte jusqu’à cet état acquiert un second souffle de vie pour une période de plusieurs milliards d’années ; on ne peut que se demander à quoi cela sert.
¶ Notes de bas de page
Ceci est illustré dans la fig. 15, la surface de la courbe à 3000 degrés n’étant qu’un seizième de la surface de la courbe à 6000 degrés. ↩︎
Les grandes images rondes d’étoiles présentées dans le frontispice résultent simplement d’une surexposition et n’ont rien à voir avec la taille des étoiles. ↩︎
Pour des raisons purement pratiques, la hauteur n’est pas considérée proportionnelle à la luminosité mais à son logarithme ; sans un tel dispositif, il serait impossible de représenter la plage de plus de 1 000 000 à 1 dans les luminosités observées des étoiles rouges. ↩︎
Ceci fournit une objection supplémentaire à l’hypothèse de Russell, qui, pour éviter toute confusion, n’a pas été mentionnée à la p. 295. ↩︎