Auteur : Sir James Jeans, MA, D. Sc., Sc. D., LL. D., FRS
[ p. 16 ]
Nous avons vu comment l’homme, après avoir habité la Terre pendant 300 000 ans, a acquis, au cours des 300 dernières années – soit le dernier millième de sa vie terrestre – un moyen optique d’étudier l’univers extérieur. Dans ce chapitre, nous tenterons de décrire les impressions qu’il a formées avec ses yeux nouvellement éveillés. Cette description sera organisée selon un ordre chronologique très approximatif. Il s’agit également d’un ordre de puissance télescopique croissante, ou encore d’une vision toujours plus lointaine dans l’espace, de sorte que notre ordre d’organisation pourrait également être décrit comme un ordre d’éloignement croissant du Soleil. Nous ne tenterons pas de tracer un récit continu, mais nous nous contenterons de mentionner quelques points de repère afin de montrer, dans les grandes lignes, l’ordre dans lequel le territoire a été conquis et consolidé dans l’étude de l’univers par l’homme.
¶ Le système solaire
Nous pouvons commencer par le système solaire, dont la structure a été dévoilée par Galilée et ses successeurs.
La famille des planètes du Soleil se divise naturellement en groupes distincts. Près du Soleil se trouvent les quatre petites planètes : Mercure, Vénus, la Terre et Mars. À des distances beaucoup plus grandes se trouvent les quatre grandes planètes : Jupiter, Saturne, Uranus et Neptune. Au-delà de toutes ces planètes se trouve la planète récemment découverte, Pluton, le membre le plus éloigné de notre système connu à ce jour.
Mercure est la plus proche du Soleil ; vient ensuite Vénus. Les orbites de ces deux planètes se situent entre l’orbite terrestre et celle du Soleil. Vues de la Terre, ces planètes semblent décrire des cercles relativement petits autour du Soleil et doivent donc nécessairement apparaître près de celui-ci dans le ciel. Par conséquent, elles ne peuvent être vues qu’au petit matin, si elles se lèvent juste avant le Soleil, ou le soir si elles se couchent après lui. Les Anciens, ne reconnaissant pas entièrement que les mêmes planètes pouvaient apparaître à la fois comme étoiles du matin et du soir, leur donnaient des noms différents selon qu’elles figuraient l’une ou l’autre. En tant qu’étoile du matin, Vénus était appelée Phosphoros par les Grecs et Lucifer par les Romains ; en tant qu’étoile du soir, elle était appelée Hespérus par les deux.
Au-delà de la Terre, s’éloignant du Soleil vers l’espace, vient Mars, complétant le groupe des petites planètes. Mars, Vénus et Mercure sont toutes plus petites que la Terre, bien que Vénus ne le soit que légèrement.
Il existe un large écart entre l’orbite de Mars, la dernière des petites planètes, et celle de Jupiter, la première des grandes planètes. Cet espace n’est pas vide ; il est occupé par les orbites de milliers de minuscules planètes appelées astéroïdes. Aucun d’entre eux n’approche la Terre en taille ; Cérès, la plus grande, ne mesure que 770 kilomètres de diamètre, et seules quatre planètes connues ont un diamètre supérieur à 160 kilomètres. Les planètes Mercure, Vénus et Mars sont connues depuis la plus haute antiquité, mais les astéroïdes n’ont fait leur apparition en astronomie qu’au XIXe siècle, Cérès, la première et la plus grande, ayant été découverte par Piazzi le 1er janvier 1801.
Au-delà des astéroïdes se trouvent les quatre grandes planètes : Jupiter, Saturne, Uranus et Neptune, toutes bien plus grandes que la Terre. Jupiter, la plus grande, a, selon Sampson, un diamètre de 142 000 km, soit plus de onze fois le diamètre de la Terre ; mille quatre cents corps de la taille de la Terre pourraient être entassés à l’intérieur de Jupiter, ce qui laisserait de la place. Saturne, qui vient ensuite, est la deuxième planète après Jupiter en taille, avec un diamètre d’environ 112 000 km. Ces deux planètes sont de loin les plus grandes.
Uranus et Neptune ont chacun un diamètre environ quatre fois supérieur à celui de la Terre, et donc un volume environ soixante-quatre fois supérieur. La taille de Pluton n’est pas encore connue avec précision, mais elle est difficilement plus grande que la Terre et probablement considérablement plus petite.
Jupiter et Saturne forment des objets célestes si remarquables qu’ils sont connus depuis les temps les plus reculés, mais Uranus et Neptune sont des découvertes relativement récentes. Sir William Herschel découvrit Uranus par hasard en 1781, alors qu’il observait avec son télescope, sans autre motif que l’espoir de trouver quelque chose d’intéressant dans le ciel. En revanche, Neptune fut découverte en 1846 grâce à des calculs mathématiques complexes, ce que beaucoup considéraient à l’époque comme le plus grand triomphe de l’esprit humain, du moins depuis l’époque de Newton. Ce fut un triomphe de jeunesse. Cet honneur doit être partagé à parts à peu près égales entre un Anglais, John Couch Adams, alors âgé de seulement 27 ans, qui fut ensuite professeur d’astronomie à Cambridge, et un jeune astronome français, Urbain J.J. Leverrier, qui n’avait que huit ans de plus que lui. Tous deux ont attribué certains caprices dans le mouvement observé d’Uranus à l’attraction gravitationnelle d’une planète extérieure, et tous deux se sont mis au travail pour calculer l’orbite sur laquelle cette supposée planète extérieure doit se déplacer pour expliquer ces caprices.
[ p. 19 ] Adams termina ses calculs le premier et informa les observateurs de Cambridge de la partie du ciel où devait se trouver la nouvelle planète. En conséquence, Neptune fut observée deux fois, sans toutefois être immédiatement identifiée comme la planète recherchée. Avant que cette identification ne soit établie à Cambridge, Leverrier avait terminé ses calculs et communiqué ses résultats à Galle, un assistant à Berlin, qui put identifier la planète immédiatement, Berlin possédant de meilleures cartes du ciel de la région en question que celles accessibles à Cambridge.
Il apparut peu à peu que l’attraction gravitationnelle de Neptune était insuffisante pour expliquer tous les aléas du mouvement d’Uranus, tandis que des aléas similaires commençaient à apparaître dans le mouvement de Neptune lui-même. Cela suggérait l’existence d’une autre planète, plus lointaine encore que Neptune. Tout comme Adams et Leverrier l’avaient fait la fois précédente, le Dr Percival Lowell, de l’observatoire de Flagstaff, en Arizona, calcula l’orbite sur laquelle la nouvelle planète supposée, la « Planète X », devait se déplacer. Mais ce n’est que récemment (en mars 1930), après de nombreuses années de recherches minutieuses, que les observateurs de Flagstaff découvrirent la planète Pluton, se déplaçant presque exactement sur l’orbite prédite par Lowell quinze ans auparavant.
Dès 1772, Bode avait établi une relation numérique simple reliant les distances des différentes planètes au Soleil. Celle-ci s’obtient comme suit : Écrivons d’abord la série de nombres.
0 1 2 4 8 16 32 64 128 256
où chaque nombre après les deux premiers est le double du précédent. Multipliez chaque nombre par trois, ce qui donne
0 3 6 12 24 48 96 192 384 768
[ p. 20 ] et ajoutez quatre à chacun, ce qui donne
4 7 10 16 28 52 100 196 388 772
Ces chiffres sont très approximativement proportionnels aux distances réelles des planètes par rapport au soleil, qui sont (en prenant la distance de la Terre comme étant de 10) :
| 3.9 | 7.2 | 10,0 | 15.2 | 26,5 | 52,0 | 95.4 | 191,9 | 300,7 | 400 |
|---|---|---|---|---|---|---|---|---|---|
| Mercure | Vénus | Terre | Mars | Astéroïdes | Jupiter | Saturne | Uranus | Neptune | Pluton |
Cette loi a été énoncée avant la découverte d’Uranus et des astéroïdes, ce qui rend remarquable leur parfaite correspondance avec les emplacements prévus. En revanche, elle est totalement erronée pour Neptune et Pluton, récemment découvert, ce qui laisse penser qu’il s’agit d’une simple coïncidence, sans explication rationnelle.
Les planètes les plus éloignées du Soleil sont extrêmement éloignées. Un habitant de Pluton, s’il existait, ne recevrait du Soleil qu’un seizième de la lumière et de la chaleur qu’un habitant de la Terre. On peut calculer que si la surface de Pluton était réchauffée uniquement par la chaleur du Soleil, sa température serait très basse, de l’ordre de -230 °C, soit plus de 400 degrés Fahrenheit.
Un télescope collecte la chaleur aussi bien que la lumière. Non seulement la capacité de captage de chaleur d’un grand télescope est considérable, mais des instruments extrêmement sensibles ont été conçus pour mesurer cette chaleur. Le télescope de 254 cm du mont Wilson serait capable de détecter la chaleur reçue par une simple bougie sur les rives du Mississippi, à 3 200 kilomètres de distance. Cette grande [ p. 21 ] sensibilité a permis de mesurer les quantités infinitésimales de chaleur reçues par des étoiles et des planètes isolées, et donc d’estimer la température de leur surface. Des mesures récentes indiquent que la surface de Jupiter est à une température d’environ -150 °C, soit à peu près la température à laquelle elle serait maintenue par la seule chaleur du Soleil. En revanche, des mesures similaires attribuent des températures de -150 °C et -170 °C respectivement à Saturne et Uranus, des températures bien plus élevées que ce à quoi on pourrait s’attendre si ces planètes n’avaient aucune source de chaleur autre que le rayonnement solaire. Mais il semble évident que toute source de chaleur interne doit être très faible, et que toutes les planètes majeures sont très froides. Il ne peut y avoir ni mers ni rivières à leur surface, puisque toute l’eau doit être gelée, et il ne peut y avoir ni pluie ni vapeur d’eau dans leur atmosphère. Il a été suggéré que les nuages qui obscurcissent notre vision de la surface de Jupiter pourraient être des particules condensées de dioxyde de carbone, ou un autre gaz dont la température d’ébullition est bien inférieure au point de congélation de l’eau.
Les conditions physiques des planètes plus petites ressemblent beaucoup à celles que nous connaissons sur Terre. Du fait de sa plus grande distance au Soleil, Mars est légèrement, mais pas énormément, plus froide que la Terre. Sa journée de 24 heures 37 minutes est à peine plus longue que la nôtre, de sorte que sa surface doit connaître des alternances de chaleur le jour et de froid la nuit, semblables à celles que nous connaissons sur Terre. Dans les régions équatoriales, la température dépasse largement le point de congélation à midi, atteignant parfois 10 °C, voire plus. Mais même ici, elle descend en dessous de zéro peu avant le coucher du soleil, et à partir de ce moment-là jusqu’à [ p. 22 ] bien plus tard le lendemain, le climat doit être très froid. Les régions polaires sont bien sûr encore plus froides, la température de la calotte neigeuse qui recouvre les pôles se situant aux alentours de -70 °C, soit -94 °F, soit 126 degrés de gel !
Vénus, plus proche du Soleil, doit avoir une température moyenne plus élevée que la Terre. Mais comme chacun de ses jours et de ses nuits correspond à plusieurs jours de notre temps terrestre, la différence de température entre le jour et la nuit doit être bien plus importante que chez nous, de sorte que sa surface doit subir de grands extrêmes de chaleur le jour et de froid la nuit. La température nocturne semble être assez uniformément égale à environ — 25 °C ou — 13 °F. En tout point de la surface de la planète, des semaines de cette température nocturne glaciale doivent alterner avec des semaines de températures diurnes torrides.
Mercure est si proche du Soleil que sa température moyenne est forcément bien plus élevée que celle de la Terre. Il ne réfléchit qu’une infime fraction – environ un quatorzième – de la lumière et de la chaleur qu’il reçoit du Soleil. Tout le reste sert à réchauffer sa surface. Plusieurs considérations suggèrent que la planète tourne toujours la même face vers le Soleil, tout comme la Lune tourne toujours la même face vers la Terre. Si tel est le cas, la moitié non chauffée de sa surface doit être extrêmement froide, et la moitié réchauffée extrêmement chaude. On peut calculer que, dans ce cas, l’hémisphère réchauffé devrait avoir une température d’environ 357 °C ; en revanche, si la planète était en rotation assez rapide, sa surface entière n’aurait qu’une température d’environ 170 °C. Tout récemment, Pettit et Nicholson ont mesuré la quantité de chaleur reçue sur Terre par l’hémisphère réchauffé et ont découvert que sa température devait être d’environ 350 °C, soit 662 °F, confirmant ainsi que la planète tourne toujours la même face vers le Soleil. Son hémisphère chaud est à une température qui fait fondre le plomb ; l’autre hémisphère, éternellement sombre et non réchauffé, est probablement plus froid que tout ce que nous pouvons imaginer.

La découverte par Galilée des quatre satellites de Jupiter fut suivie de la découverte que chaque planète était accompagnée de satellites, à l’exception des deux dont les orbites se situaient à l’intérieur de celle de la Terre. En 1655, Huyghens découvrit Titan, le plus grand satellite de Saturne, et en 1684, Cassini en avait découvert quatre autres. Puis, un siècle plus tard, Sir William Herschel découvrit deux satellites d’Uranus en 1787 et deux autres satellites de Saturne en 1789. Nous aborderons l’ensemble du système des satellites planétaires ainsi que les corps plus petits du système solaire – comètes, météores et étoiles filantes – dans un chapitre ultérieur, lorsque nous aborderons leur genèse.
¶ Le système galactique
Notre prochain jalon est l’étude des étoiles par les deux Herschel, Sir William Herschel, le père (1738-1822) et Sir John Herschel, le fils (1792-1871). Ce que Galilée avait fait pour le système solaire, les deux Herschel s’apprêtaient à le faire pour l’immense famille d’étoiles – le système « galactique », délimité par la Voie lactée – dont notre Soleil fait partie.
Par une nuit claire et sans lune, la Voie lactée s’étend, telle une grande arche de faible lumière, d’un horizon à l’autre. Elle n’est qu’une partie d’un cercle lumineux complet – le cercle galactique – qui entoure la Terre et divise le ciel en deux moitiés égales, formant une sorte d’« équateur » céleste, par rapport auquel les astronomes ont l’habitude de mesurer la latitude et la longitude du ciel. Le télescope de Galilée avait démontré qu’elle était constituée d’une multitude d’étoiles faibles, chacune trop faible pour être observée individuellement sans télescope (voir Planche I). Et, comme on pouvait s’y attendre, l’interprétation correcte de cette grande ceinture d’étoiles faibles s’est avérée fondamentale pour comprendre l’architecture de l’univers.
Si les étoiles étaient dispersées uniformément dans l’espace infini, nous finirions par en trouver une, quelle que soit la direction de notre regard, de sorte que le ciel apparaîtrait comme un flamboiement uniforme d’une lumière insupportable. Il est vrai que ce ne serait pas le cas si la lumière était atténuée ou masquée après un certain trajet, mais même dans ce cas, le ciel apparaîtrait identique dans toutes les directions, car il n’y aurait aucune raison pour qu’une partie du ciel soit plus richement constellée d’étoiles qu’une autre. Ainsi, l’existence de la Voie lactée démontre que le système stellaire ne s’étend pas uniformément à l’infini. Il doit avoir une structure définie, et c’est l’architecture de celle-ci que Sir William Herschel s’est attaché à décrypter. Les travaux qu’il a menés pour la moitié nord du ciel ont ensuite été étendus à l’hémisphère sud par son fils, Sir John Herschel.
Nous comprendrons mieux la méthode employée par les Herschel si nous imaginons d’abord que toutes les étoiles du ciel sont des objets intrinsèquement similaires. Chacune émettrait alors la même quantité de lumière, de sorte que les étoiles les plus proches apparaîtraient brillantes et les étoiles les plus éloignées faibles, simplement sous l’effet de la distance. La façon dont la luminosité apparente diminue avec la distance est bien connue ; la loi est celle de l’« inverse du carré de la distance », ce qui signifie que la luminosité apparente diminue aussi rapidement que le carré de sa distance augmente ; une étoile deux fois plus éloignée [ p. 25 ] qu’une seconde étoile semblable n’apparaît que quatre fois moins brillante, et ainsi de suite. Ainsi, si toutes les étoiles émettaient la même quantité de lumière, nous pourrions estimer les distances relatives de deux étoiles quelconques dans le ciel à partir de leurs luminosités relatives. En coupant des fils de longueurs proportionnelles à la distance des différentes étoiles et en les pointant dans la direction des étoiles auxquelles ils se rapportent, nous pourrions modéliser la disposition des étoiles dans le ciel. Nous connaîtrions ainsi la structure complète du système stellaire, à l’exception de son échelle. Pour représenter les étoiles faibles de la Voie lactée, il faudrait un grand nombre de fils très longs. Dans le modèle, ils pointeraient tous vers différentes parties de la Voie lactée, formant une structure plate en forme de roue.
Le problème auquel Sir William Herschel était confronté était plus complexe, car il savait que les étoiles avaient des luminosités intrinsèques différentes et se trouvaient à des distances différentes, et que ces deux facteurs se combinaient pour produire des différences de luminosité apparente. L’une des principales difficultés de l’astronomie, tant pour les Herschel que pour l’astronome d’aujourd’hui, réside dans la nécessité de démêler ces deux facteurs avant de parvenir à des conclusions définitives.
Herschel a constaté que le nombre d’étoiles visibles dans le champ de son télescope variait énormément selon les directions de l’espace. Il était bien sûr maximal lorsque le télescope était pointé vers la Voie lactée, et diminuait régulièrement et rapidement à mesure que le télescope s’en éloignait. En général, deux champs de télescopes situés à égale distance de la Voie lactée contenaient à peu près le même nombre d’étoiles. Dans le langage technique de l’astronomie, la richesse du champ stellaire dépendait principalement de la latitude galactique, tout comme le climat terrestre dépend principalement de la latitude géographique, et peu de la longitude.
On a constaté que les champs situés à différentes distances de la Voie lactée différaient en qualité et en nombre d’étoiles. Les étoiles les plus brillantes étaient présentes à peu près également dans tous les champs, la différence de champ résultant principalement des étoiles faibles, et en particulier des étoiles les plus faibles, devenant énormément plus abondantes à mesure que l’on approchait de la Voie lactée.
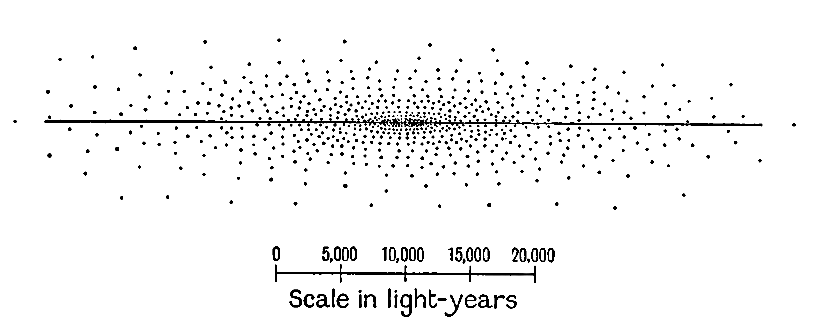
Sir William Herschel interpréta à juste titre ce phénomène comme la preuve que le système d’étoiles entourant le Soleil commençait à s’éclaircir aux distances atteintes par son télescope, et que cette raréfaction était plus rapide dans les directions les plus éloignées de la Voie Lactée. Il supposait que la forme générale du système stellaire galactique était celle d’une brioche, d’un biscuit ou d’une montre, les étoiles étant plus denses près du centre et plus éparses dans les régions périphériques. Le plan de la Voie Lactée formait bien sûr le plan central de la structure. Le fait que la Voie Lactée divise le ciel en deux moitiés presque parfaitement égales lui suggérait que le Soleil devait se trouver très près de ce plan central, ce que confirment les récentes recherches très approfondies de Seares, van Rhijn et d’autres. Du fait que des parties du ciel équidistantes de la Voie Lactée apparaissaient à peu près aussi brillantes, Herschel en déduisit que le Soleil se trouvait non seulement dans le plan central du système, mais aussi très proche de son centre réel. Cette opinion a prévalu jusqu’à une époque récente, mais les recherches de Shapley et d’autres montrent maintenant qu’elle est intenable (voir p. 65 ci-dessous).
Fig. 1 montre une coupe transversale du type général de structure que Sir William Herschel attribuait au système galactique, bien que la distribution détaillée des étoiles [ p. 27 ] représentée sur le diagramme soit celle donnée beaucoup plus tard (1922) par Kapteyn. On comprend aisément comment une structure de ce type pourrait expliquer l’aspect général du ciel. Les étoiles qui apparaissent les plus brillantes sont, en général, les plus proches ; elles sont si proches qu’aucun amincissement notable des étoiles ne se produit à cette distance. C’est pourquoi les étoiles très brillantes sont présentes en nombre à peu près égal dans toutes les directions. Les étoiles qui apparaissent très faibles sont pour la plupart très éloignées, si éloignées que la grande profondeur du système dans les directions situées à l’intérieur ou à proximité du plan galactique entre en jeu. Dans de telles directions, couche après couche d’étoiles, disposées presque à l’infini les unes derrière les autres, donnent naissance à la concentration apparente d’étoiles faibles que nous appelons la Voie Lactée.
L’acceptation finale de la conception copernicienne de la structure du système solaire est due en grande partie à la découverte par Galilée du système similaire de Jupiter, situé dans l’espace de telle sorte qu’un observateur terrestre pouvait en obtenir une vue d’ensemble. Nous ne pouvons jamais obtenir une vue d’ensemble du système solaire, car nous ne pouvons l’observer que de l’intérieur. La preuve optique de l’existence de tels systèmes ne pouvait donc provenir que de la découverte d’autres systèmes similaires, visibles de l’extérieur.
Sir William Herschel pensait avoir confirmé sa propre vision de la structure du système galactique de la même manière, en découvrant des systèmes similaires, dont il pouvait obtenir une vue aérienne car ils étaient entièrement extérieurs à la galaxie. Il qualifiait ces objets d’« univers insulaires » et les considérait comme des nuages d’étoiles. Leur apparence nébulaire était brumeuse et, bien qu’il fût impossible d’en distinguer les étoiles, il pensait qu’une puissance télescopique suffisante le permettrait, tout comme elle avait permis à Galilée d’observer les étoiles de la Voie lactée. Ces objets, que nous allons décrire presque immédiatement, sont généralement appelés « nébuleuses extragalactiques » en raison de leur position, bien que nous trouverions souvent plus commode d’utiliser le terme plus court de « grandes nébuleuses », auquel leur immense taille leur donne pleinement droit.
¶ Nébuleuses
Un télescope présente une planète comme un disque de taille appréciable, et un oculaire grossissant 60 fois fera paraître Jupiter aussi gros que la Lune. Pourtant, un oculaire grossissant 60 fois, ou un nombre de fois supérieur, ne pourra jamais faire paraître une étoile aussi grosse que la Lune. Aucun grossissement à notre portée ne fait apparaître une étoile autrement que comme un simple point lumineux. Les étoiles sont bien sûr infiniment plus grandes que Jupiter, mais elles sont aussi infiniment plus éloignées, et c’est la distance qui prime.
Le télescope montre néanmoins un certain nombre d’objets qui paraissent plus grands que de simples points lumineux. [ p. 29 ] Ils ont généralement une apparence faible et brumeuse, et ont donc reçu le nom général de « nébuleuses ». Une étude détaillée a montré qu’ils se répartissent en trois classes distinctes.
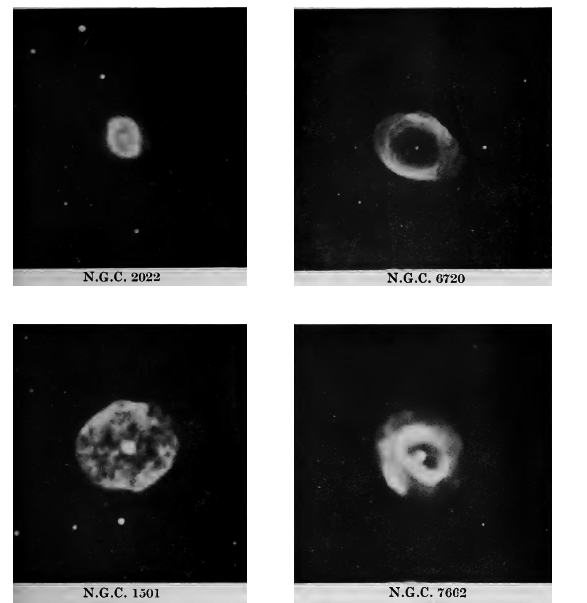

Nébuleuses planétaires. La première classe est généralement décrite comme « Nébuleuses planétaires ». Elles n’ont rien de planétaire, si ce n’est que, comme les planètes, elles apparaissent comme des disques finis dans un télescope. On ne connaît que quelques centaines de ces objets, quatre exemples typiques étant illustrés dans la Planche II. Elles se situent toutes dans le système galactique. Nous discuterons de leur structure physique plus loin (p. 321). Pour l’instant, il suffit de dire qu’elles sont probablement de la nature d’étoiles qui se sont, d’une manière ou d’une autre, entourées d’atmosphères lumineuses d’une étendue considérable. Si tel est le cas, elles contredisent bien sûr notre affirmation générale selon laquelle aucune étoile n’apparaît jamais autrement que comme un point lumineux dans un télescope ; nous devons faire une exception en faveur des nébuleuses planétaires.
Nébuleuses galactiques. La deuxième classe est généralement décrite comme « nébuleuses galactiques », des exemples étant présentés dans les Planches III, VI (p. 37) et VII (p. 44). Leur forme est totalement irrégulière. Leur apparence générale est celle d’énormes volutes de gaz incandescentes s’étendant d’une étoile à l’autre, et c’est en fait à peu près ce qu’elles sont. Comme les nébuleuses planétaires, elles se situent entièrement dans le système galactique. Un simple coup d’œil montre que chaque nébuleuse irrégulière contient plusieurs étoiles enchevêtrées ; un examen télescopique minutieux étend souvent les dimensions de la nébuleuse presque indéfiniment, de sorte que nous pouvons avoir la quasi-totalité d’une constellation enveloppée dans une seule nébuleuse.
Il n’y a guère de doute quant à la nature physique de ces nébuleuses. L’espace entre les étoiles n’est pas totalement vide de matière, mais occupé par un mince nuage de gaz d’une ténuité presque indescriptible. Ça et là, ce nuage peut être plus dense que d’habitude ; çà et là, il peut être illuminé et rendu incandescent par le rayonnement des étoiles qu’il contient. Ailleurs, il peut être totalement opaque à la lumière, tel un rideau noir qui traverse le ciel. La combinaison des variations de densité, d’opacité et de luminosité produit toutes les formes fantastiques et les différents degrés de lumière et d’ombre que nous observons dans les nébuleuses galactiques.
Cette même opacité est responsable des taches sombres qui apparaissent dans la disposition générale des étoiles. Un exemple frappant se trouve dans la partie de la Voie lactée représentée sur la Planche I (p. 23). Cette tache sombre, qui ressemble à première vue à un trou dans le système stellaire, est décrite graphiquement comme « le sac de charbon ». Ces taches noires dans le ciel ne peuvent représenter de véritables trous, car il est inconcevable qu’il y ait autant de tunnels vides à travers les étoiles, tous pointés exactement vers la Terre, de sorte que nous sommes contraints de les interpréter comme des voiles de matière obscurcissante qui atténuent ou éteignent la lumière des étoiles situées derrière elles.
Nébuleuses extragalactiques. La troisième classe de nébuleuses est d’une nature totalement différente. Leurs membres ont pour la plupart une forme définie et régulière, et présentent diverses autres caractéristiques qui les rendent faciles à identifier. On les appelait autrefois « nébuleuses blanches » en raison de la qualité de la lumière qu’elles émettaient. Plus tard, le télescope géant de 1,80 mètre de Lord Rosse révéla que nombre d’entre elles avaient une structure spirale ; on les appela « nébuleuses spirales ». La plus remarquable de toutes les nébuleuses spirales est la Grande Nébuleuse M 31 d’Andromède, représentée sur la Planche IV, qui est tout juste visible [ p. 31 ] à l’œil nu. Marius, l’observant au télescope en 1612, la décrivit comme ressemblant à « la lumière d’une bougie vue à travers une corne ». Planche V montre un deuxième exemple, probablement de structure très similaire, qui est vu sous un autre angle, de manière à apparaître presque exactement de côté.


Il est désormais largement prouvé que les nébuleuses de ce type se situent toutes en dehors du système galactique, de sorte que le terme « nébuleuses extragalactiques » les décrit parfaitement. Leur taille est colossale. Il faudrait agrandir l’une ou l’autre des photographies des planches IV et V à la taille de l’Europe entière pour qu’un corps de la taille de la Terre y soit visible, même sous un microscope puissant. Leur forme générale est similaire à celle que Sir William Herschel attribuait au système galactique, et c’est ce qui l’a initialement conduit à les considérer comme des « univers-îles » similaires au système galactique. Nous verrons plus loin dans quelle mesure sa conjecture a été confirmée par des recherches récentes.
¶ Les distances des étoiles
L’année 1838 constitue notre prochain jalon ; c’est l’année où la distance d’une étoile a été mesurée pour la première fois.
Au IIe siècle après Jésus-Christ, Ptolémée avait soutenu que si la Terre se déplaçait dans l’espace, sa position par rapport aux étoiles environnantes devait changer continuellement. Comme la Terre tournait autour du Soleil, ses habitants se trouvaient dans la position d’un enfant sur une balançoire. Et, tout comme l’enfant qui se balance voit les arbres, les personnes et les maisons les plus proches osciller rythmiquement sur un fond lointain de collines et de nuages, les habitants de la Terre devraient voir les étoiles les plus proches changer continuellement de position sur leur [ p. 32 ] fond d’étoiles plus lointaines. Pourtant, nuit après nuit, les constellations restaient les mêmes, du moins c’est ce que soutenait Ptolémée ; les mêmes étoiles tournaient éternellement dans les mêmes positions relatives autour du pôle, et des groupes d’étoiles remarquables comme les sept étoiles de la Grande Ourse, les Pléiades ou la constellation d’Orion ne présentaient aucun signe de changement. Pour autant que l’œil humain sans aide puisse le dire, les étoiles pourraient être des taches de peinture lumineuse sur un fond de toile, avec la terre comme pivot immobile autour duquel toute la structure oscille.
À l’opposé, la théorie copernicienne exigeait bien sûr que les étoiles les plus proches se déplacent sur le fond des étoiles les plus lointaines, à la manière dont la Terre accomplissait son tour annuel autour du Soleil. Pourtant, année après année, et même siècle après siècle, aucun mouvement de ce genre n’a été détecté. La vieille thèse ptolémaïque selon laquelle la Terre formait le centre fixe de l’univers aurait presque pu retrouver sa place antérieure, si divers éléments n’avaient commencé à démontrer que même les étoiles les plus proches étaient nécessairement très éloignées, si éloignées, en fait, que leur absence apparente de mouvement ne devait pas surprendre. Un enfant sur une balançoire ne peut espérer avoir une preuve optique de son mouvement si l’objet le plus proche qu’il peut voir se trouve à trente kilomètres.
Très peu d’étoiles apparaissent plus brillantes que Saturne à son apogée ; elle paraît à peu près aussi brillante qu’Altaïr, la onzième étoile la plus brillante du ciel. Pourtant, Saturne ne brille que par la lumière qu’elle réfléchit du Soleil, et sa distance au Soleil est telle qu’elle ne reçoit qu’environ une partie sur 2 500 millions de la lumière totale émise par le Soleil. Et, comme la surface de Saturne ne réfléchit qu’environ les deux cinquièmes de la lumière qu’elle reçoit, il s’ensuit que Saturne ne brille que d’un 6 000 millionième de la lumière du Soleil. Si, comme Kepler et d’autres l’avaient soutenu, Altaïr était essentiellement semblable au Soleil, sa puissance en bougies serait probablement à peu près la même que celle du Soleil et émettrait donc environ 6 000 millions de fois plus de lumière que Saturne. Le fait qu’Altaïr et Saturne apparaissent à peu près aussi brillants dans le ciel ne peut signifier qu’Altaïr est 80 000 fois plus éloignée que Saturne[1]. Cet argument est essentiellement identique à celui avancé par Newton dans son Système du Monde pour démontrer que même les étoiles les plus brillantes, comme Altaïr, doivent être très éloignées.
Et tel fut le cas. Tous les efforts pour découvrir le mouvement d’oscillation apparent des étoiles – « mouvement parallactique », comme on l’appelle techniquement – résultant du mouvement orbital de la Terre échouèrent jusqu’en 1838, lorsque trois astronomes, Bessel, Henderson et Struve, détectèrent presque simultanément les mouvements parallactiques des trois étoiles : 61 Cygni, α Centauri et α Lyrae respectivement. L’ampleur de leur mouvement parallactique permit de calculer les distances des étoiles, de sorte que les habitants de la Terre furent non seulement en possession d’une preuve oculaire certaine qu’elles tournaient autour du Soleil, mais, grâce aux effets visibles de cette oscillation, ils purent calculer les distances des étoiles les plus proches. Les valeurs calculées n’étaient pas exactes selon les normes modernes, mais elles fournissaient les premières estimations précises de l’échelle à laquelle l’univers est construit.
Arrêtons-nous un instant pour examiner comment cette échelle est construite. La première étape consiste à choisir une ligne de base pratique de quelques kilomètres de long à la surface de la Terre, [ p. 34 ], et à la mesurer en yards ou en mètres standard. À partir de cette ligne de base, un levé géodésique cartographie une longue bande étroite de la surface terrestre, de préférence orientée nord-sud. La différence de latitude aux deux extrémités est ensuite mesurée par des méthodes astronomiques, par exemple en observant la différence d’altitude de l’étoile polaire aux deux endroits. La longueur de la bande étant déjà connue en miles, cela donne immédiatement les dimensions de la Terre. Selon Hayford (1909), le rayon équatorial de la Terre est de 6378,388 kilomètres, soit 3963,34 miles, son rayon polaire étant de 6356,909 kilomètres, soit 3949,99 miles.
L’étape suivante consiste à déterminer la taille du système solaire par rapport à celle de la Terre. Lorsque le Soleil est éclipsé par la Lune, l’heure à laquelle la Lune commence à recouvrir le disque solaire diffère selon les stations terrestres, et les différences de temps observées nous permettent de mesurer la distance de la Lune par rapport aux distances connues à la surface de la Terre. Ainsi, la distance moyenne de la Lune est de 384 403 kilomètres, soit 238 857 miles. De même, le transit de la planète Vénus devant le disque solaire permet de déterminer l’échelle du système solaire par rapport aux dimensions de la Terre. L’astéroïde Éros offre des perspectives encore plus prometteuses. La Conférence de Paris (1911) a adopté 149 450 000 kilomètres, soit 92 870 000 miles, comme valeur la plus probable pour la distance moyenne de la Terre au Soleil. L’étape suivante et finale, qui s’est accomplie en 1838, consiste à utiliser le diamètre de l’orbite terrestre comme ligne de base et à déterminer les distances des étoiles.
La première étape, du yard ou du mètre standard à la ligne de base mesurée à la surface de la Terre, implique une augmentation de plusieurs milliers de fois de la longueur. L’augmentation impliquée dans l’étape suivante, de la ligne de base au diamètre de la Terre, est à nouveau de plusieurs milliers. Et encore une fois, l’étape suivante, du diamètre de la Terre à celui de l’orbite terrestre, implique une augmentation de plusieurs milliers. Mais la dernière étape de toutes, de l’orbite terrestre aux distances stellaires, implique une augmentation d’un million de fois.
Des mesures récentes montrent que les étoiles les plus proches se trouvent à près d’un million de fois la distance des planètes les plus proches. Au plus près de la Terre, Vénus est à 42 millions de kilomètres, tandis que l’étoile la plus proche, Proxima du Centaure, est à 40 millions de kilomètres ; cette dernière est une faible compagne de la célèbre étoile brillante du Centaure, dans l’hémisphère sud. Les distances des planètes au plus près, et celles des étoiles les plus proches, sont indiquées dans le tableau suivant :
| Planètes | Étoiles | |||
|---|---|---|---|---|
| Nom | Distance (miles) | Nom | Distance (miles) | Distance (années-lumière) |
| Vénus | 26 000 000 | Proxima du Centaure Centaure |
25 000 000 millions | 4,27 4,31 |
| Mars | 35 000 000 | Munich 15040 | 36 000 000 „ | 6,06 |
| Mercure | 47 000 000 | Wolf 359 Lalande 21185 Sirius |
47 000 000 „ 49 000 000 „ 51 000 000 „ |
8,07 8,33 8,65 |
Comme il est presque impossible d’en visualiser un million, la simple affirmation selon laquelle les étoiles sont un million de fois plus éloignées que les planètes ne donne qu’une faible indication de l’immensité du fossé qui sépare le système solaire de ses plus proches voisins dans l’espace. L’apparente fixité des étoiles donne peut-être une impression plus frappante.
La Terre effectue son tour annuel autour du Soleil à une vitesse d’environ 30 kilomètres par seconde, soit environ 1 200 fois la vitesse d’un train express. Le Soleil se déplace à travers les étoiles à peu près à la même vitesse – pour être précis, à environ 800 fois la vitesse d’un train express. Et, en gros, les planètes les plus proches et la majorité des étoiles se déplacent à des vitesses similaires. Nous n’obtiendrons pas une mauvaise approximation de la vérité si nous imaginons que tous les corps astronomiques se déplacent à des vitesses exactement égales, disons, pour fixer nos pensées, une vitesse égale à 1 000 fois la vitesse d’un train express. Les distances des objets astronomiques sont maintenant trahies par la vitesse à laquelle ils semblent se déplacer dans le ciel – plus leur mouvement apparent est lent, plus leurs distances sont grandes, et vice versa. Or, les planètes se déplacent dans le ciel si rapidement qu’il est assez facile de détecter leur mouvement d’une nuit à l’autre et même d’une heure à l’autre ; Les étoiles se déplacent si lentement que, sans l’aide d’un télescope, aucun mouvement ne peut être détecté de génération en génération, ni même d’âge en âge. Même les constellations les plus remarquables du ciel, généralement constituées d’étoiles proches, ont conservé leur aspect actuel tout au long de l’histoire. Le contraste entre les planètes qui changent de position toutes les heures et les étoiles qui ne montrent aucun changement notable en un siècle, donne une impression saisissante de l’éloignement des étoiles par rapport aux planètes.
Il est bien plus difficile de visualiser les distances réelles des étoiles. L’affirmation selon laquelle même la plus proche d’entre elles se trouve à 40 millions de kilomètres ne donne guère d’image précise, mais nous pourrions obtenir de meilleurs résultats [ p. 37 ] en affirmant que la distance est de 4,27 années-lumière, soit la distance que la lumière, voyageant à 300 000 kilomètres par seconde, met 4,27 ans à parcourir.

La lumière se propage à la même vitesse que les signaux sans fil, car tous deux sont des ondes de perturbation électrique. Soit dit en passant, cette vitesse est environ un million de fois supérieure à celle du son. L’énorme disparité entre les vitesses du son et des ondes électriques est clairement mise en évidence par le processus ordinaire de radiodiffusion. Lorsqu’un orateur diffuse depuis Londres, sa voix met plus de temps à parcourir un mètre de sa bouche jusqu’au microphone sous forme d’onde sonore, qu’à parcourir les 900 kilomètres supplémentaires jusqu’à Berlin ou Milan sous forme d’onde électrique. Les auditeurs sans fil en Australie entendent la musique d’un concert diffusé plus tôt qu’un auditeur ordinaire au fond de la salle, qui se fie uniquement au son ; ils l’entendent un quinzième de seconde après sa diffusion. Pourtant, la lumière, ou les ondes sans fil se propageant à la même vitesse que la lumière, met 4,27 ans pour atteindre l’étoile la plus proche, de sorte que les habitants de Proxima du Centaure auraient plus de quatre ans et quart de retard pour entendre un concert terrestre. Et avec le temps, il nous faudra considérer d’autres étoiles encore plus lointaines que la musique terrestre n’aurait pas encore atteintes si elle avait commencé son voyage avant la conquête normande, avant la construction des pyramides, avant même l’apparition de l’homme sur terre.
¶ L’époque photographique
Si nous ne devions retenir qu’un seul jalon dans le progrès de l’astronomie, nous pourrions bien choisir l’application de la photographie à l’astronomie dans les dernières années du XIXe siècle ; cela a ouvert les portes du progrès plus complètement que tout autre progrès depuis l’invention du télescope. Jusqu’alors, le télescope, après avoir collecté et courbé les rayons lumineux du ciel, avait projeté le faisceau concentré de lumière à travers la pupille de l’œil humain sur la rétine ; il devait désormais le projeter sur la plaque photographique, incomparablement plus sensible. L’œil ne peut retenir une impression que pendant une fraction de seconde ; la plaque photographique additionne toutes les impressions qu’elle reçoit pendant des heures, voire des jours, et les enregistre pratiquement pour toujours. L’œil ne peut mesurer les distances entre les objets astronomiques qu’à l’aide d’un mécanisme complexe de fils transversaux, de vis et de verniers ; la plaque photographique enregistre les distances automatiquement. L’œil, trahi par des idées préconçues, l’impatience ou l’espoir, peut commettre et commet toutes les erreurs imaginables ; l’appareil photo ne peut pas mentir.
Ainsi, si l’on tente de repérer des points de repère dans l’astronomie du XXe siècle, on découvre qu’elle ne se résume en quelque sorte qu’à des points de repère ; les méthodes de conquête lentes et ardues du XIXe siècle ont donné lieu à une sorte de ruée vers l’or : on jalonne les concessions, on gratte la surface, on recueille les pépites les plus remarquables et on abandonne les fouilles pour des découvertes plus prometteuses, le tout avec une telle rapidité que toute tentative de description de la situation est dépassée presque avant même d’avoir pu être publiée. Nous ne pouvons que tenter de donner une impression générale du nouveau territoire, et à celle-ci se mêlera inextricablement une discussion sur l’ancien territoire à la lumière des nouvelles connaissances.
[ p. 39 ]
¶ Groupes d’étoiles et systèmes binaires
Un coup d’œil au ciel, ou mieux, une photographie d’un fragment de ciel, suggère que, globalement, les étoiles sont dispersées au hasard, à l’exception d’une concentration d’étoiles faibles dans et vers la Voie lactée, que nous avons déjà examinée. Chaque petit morceau de ciel ne semble pas très différent de ce qu’il serait si des étoiles brillantes et faibles avaient été dispersées au hasard dans un poivrier céleste.
Mais ce n’est pas tout. Ça et là, on observe des groupes d’étoiles remarquables, qui ne peuvent guère être le fruit du hasard. La ceinture d’Orion, les Pléiades, la chevelure de Bérénice, et même la Grande Ourse elle-même, ne semblent pas être des accidents, et en réalité, ce n’est pas le cas. C’est l’existence de ces groupes naturels d’étoiles qui est à l’origine et justifie la division des étoiles en constellations. Nous expliquerons plus loin comment les propriétés physiques des étoiles sont étudiées ; pour l’instant, il suffit de remarquer que l’étude physique confirme l’hypothèse selon laquelle des groupes tels que ceux mentionnés précédemment constituent, en général, de véritables familles, et non de simples rassemblements accidentels d’étoiles. Les étoiles d’un même groupe, comme les Pléiades, présentent non seulement les mêmes propriétés physiques, mais aussi des mouvements spatiaux identiques, voyageant ainsi perpétuellement dans le ciel en compagnie les unes des autres. Comme un tel groupe d’étoiles est à la fois physiquement semblable et voyageant en compagnie, on pourrait à juste titre le décrire comme une famille d’étoiles. L’astronome préfère cependant les appeler un « amas en mouvement ».
Ces familles sont de presque toutes les tailles, le plus petit [ p. 40 ] et le plus courant ne comportant que deux membres. Ensuite, le type le plus courant est composé de trois membres ; nos trois plus proches voisins dans l’espace, Proxima du Centaure et les deux étoiles d’une étoile du Centaure, forment un tel système triple. Viennent ensuite les systèmes de quatre, cinq et six membres, et ainsi de suite indéfiniment.
Intéressons-nous d’abord aux familles composées de seulement deux membres – les « systèmes binaires », comme on les appelle généralement. Même si les étoiles avaient été dispersées dans le ciel au hasard, les lois du hasard exigeraient que, dans un certain nombre de cas, des paires d’étoiles apparaissent très proches. Et l’étude d’une photographie de n’importe quel champ d’étoiles montre qu’un grand nombre de telles paires proches existent réellement. Ce nombre est cependant plus grand que ce que les seules lois du hasard peuvent expliquer. Certaines paires d’étoiles peuvent être proches l’une de l’autre par accident, mais une cause physique est nécessaire pour expliquer les autres. Nous pouvons percer le mystère en photographiant le champ à intervalles de quelques années et en comparant les différents résultats obtenus. Certaines des étoiles qui apparaissaient initialement comme des paires proches s’éloignent progressivement. Ce sont les paires d’étoiles qui, bien qu’apparaissant proches dans le ciel, ne l’étaient pas dans l’espace ; une étoile se trouvait simplement presque exactement alignée avec l’autre vue de la Terre. D’autres paires ne se disloquent pas avec le temps ; Les deux composantes changent de position relative, mais ne se séparent jamais complètement. Dans le cas le plus simple, on peut constater qu’une étoile décrit une orbite approximativement circulaire autour de l’autre, tout comme la Terre autour du Soleil et la Lune autour de la Terre, et ce pour la même raison : la gravitation les maintient ensemble.
[ p. 41 ]
La loi de la gravitation. Laissez tomber une balle de cricket et elle retombe. On dit que la cause de sa chute est l’attraction gravitationnelle de la Terre. De même, une balle de cricket lancée en l’air ne se déplace pas indéfiniment dans la direction où elle est lancée ; si c’était le cas, elle quitterait définitivement la Terre et s’envolerait dans l’espace. Elle est sauvée de ce sort par l’attraction gravitationnelle de la Terre qui l’entraîne progressivement vers le bas, de sorte qu’elle retombe sur Terre. Plus on la lance vite, plus elle parcourt de distance avant que cela ne se produise ; une balle similaire lancée par un fusil parcourrait des kilomètres avant d’être ramenée sur Terre.
La loi qui régit tous ces phénomènes est simple. Elle est la suivante : l’attraction gravitationnelle terrestre fait chuter tous les corps de 5 mètres vers la Terre en une seconde. Ceci est vrai pour tous les corps libres de chuter, quel que soit leur mouvement ; tout corps qui n’est pas retenu d’une manière ou d’une autre par la gravitation est 5 mètres plus bas à la fin de chaque seconde que ce qu’il aurait été si la gravitation n’avait pas agi pendant cette seconde.
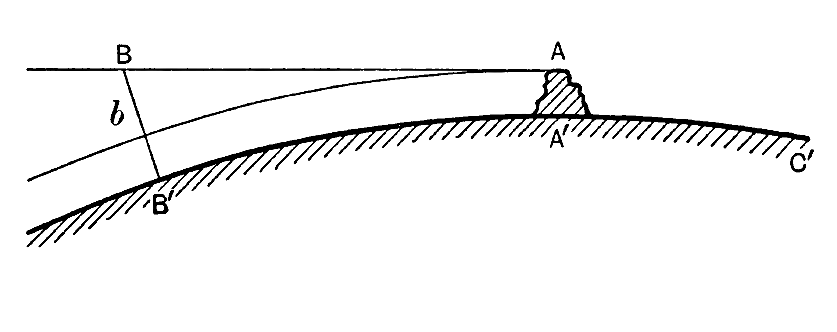
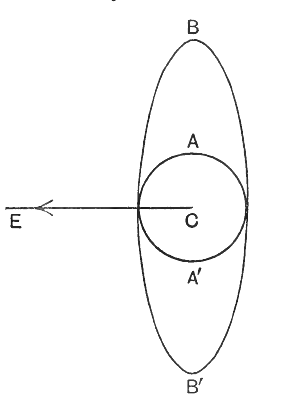
Pour illustrer ce que cela signifie, supposons que la grande courbe circulaire B’A’C de la fig. 2 représente la surface de la Terre, et imaginons qu’un coup de feu soit tiré horizontalement depuis A, le sommet d’une élévation AA’. Si le coup n’était pas attiré vers la Terre par la gravitation, il se déplacerait indéfiniment [ p. 42 ] le long de la ligne AB dans l’espace. Si AB est la distance qu’il parcourrait en une seconde dans ces conditions imaginaires, la fin de son vol réel ne le trouve pas en B, mais en un point situé à 5 mètres plus près de la Terre, la gravitation l’ayant attiré vers le bas de ces 5 mètres pendant son vol. Par exemple, si BB’ de la fig. 2 se trouvait à 5 mètres, le coup frapperait la Terre en B’ après un vol d’exactement une seconde.
Prenons un autre exemple : supposons que la chute de 5,8 mètres sous B n’entraîne pas le boulet vers le sol, mais seulement vers un point b, situé exactement à la même hauteur au-dessus de la surface terrestre que le point A d’où il a décollé. Si la gravitation n’agissait pas, de sorte que le boulet suivait la ligne AB, sa hauteur au-dessus de la Terre augmenterait continuellement. En réalité, dans le cas qui nous occupe, la gravitation tire le boulet vers le bas à une vitesse telle qu’elle neutralise l’augmentation de hauteur qui se produirait autrement, de sorte que la hauteur du boulet n’augmente ni ne diminue ; il ne s’envole pas dans l’espace ni ne retombe sur Terre, mais continue à décrire des cercles autour de la Terre indéfiniment.
Un simple calcul géométrique montre que pour que la distance Bb soit de 16 pieds, la distance parcourue par AB en une seconde doit être de 25 880 pieds, soit 4,90 miles[^2]. Ainsi, si l’on pouvait tirer un coup de feu horizontalement à une vitesse de 4,90 miles par seconde, il décrirait des cercles sans fin autour de la Terre, l’attraction gravitationnelle terrestre neutralisant exactement la tendance naturelle du coup à s’éloigner le long de la ligne droite AB.
En 1665, Newton commença à soupçonner que cette même attraction gravitationnelle pouvait être la cause pour laquelle la Lune [ p. 43 ] décrivait une orbite circulaire autour de la Terre au lieu de s’éloigner tangentiellement dans l’espace. La distance de la Lune au centre de la Terre est de 382 857 kilomètres, soit 60,27 fois le rayon de la Terre. Comme la Lune décrit un cercle de cette taille chaque mois (27 jours, 4 heures, 43 minutes, 11,5 secondes), on peut calculer que sa vitesse sur son orbite est de 3688 kilomètres par heure. Au bout d’une seconde, elle aura parcouru 1 028 mètres, et si elle maintenait une trajectoire strictement rectiligne, cela l’éloignerait de 0,0044 mètre de la Terre. Ainsi, pour maintenir une orbite circulaire exacte autour de la Terre, elle doit chuter de 0,0044 mètre en une seconde. C’est bien moins que la vitesse de chute d’un corps à la surface de la Terre en une seconde, mais Newton a supposé que la force de gravité devait faiblir à mesure que nous nous éloignions de la surface de la Terre. En réalité, un corps à la surface de la Terre tombe 3 632 fois plus vite que la Lune sur son orbite. Or, 3 632 est le carré de 60,27 (ou 3 632 = 60,27 x 60,27), d’où Newton a vu que la chute de la Lune serait exactement la bonne si la force de gravité diminuait comme l’inverse du carré de la distance, c’est-à-dire si elle diminuait aussi rapidement que le carré de la distance augmentait. Comme nous le verrons plus loin, l’observation astronomique confirme la véracité de cette loi de multiples façons. Cela a conduit Newton à proposer sa célèbre loi de la gravitation selon laquelle l’attraction gravitationnelle de tout corps, comme la Terre, diminue inversement au carré de la distance du corps.
Le professeur C.V. Boys et d’autres ont mesuré en laboratoire l’attraction gravitationnelle exercée par quelques tonnes de plomb. Grâce à ces données, il est facile de calculer combien de tonnes la Terre doit contenir pour exercer l’attraction gravitationnelle observée sur les corps extérieurs. On constate que le poids de la Terre doit être légèrement inférieur à six milliards de milliards de tonnes[2], soit, comme nous l’écrirons, 6 x 1021 tonnes[^4].
Tout comme l’attraction gravitationnelle de la Terre fait que la Lune décrit perpétuellement des cercles autour d’elle, l’attraction gravitationnelle du Soleil fait que la Terre et toutes les autres planètes décrivent des cercles autour du Soleil. Connaissant la distance d’une planète au Soleil, ainsi que sa vitesse sur son orbite, nous pouvons calculer la distance parcourue par cette planète vers le Soleil en une seconde. Cela nous indique l’intensité de l’attraction gravitationnelle du Soleil, et nous pouvons en déduire que son poids doit être [ p. 45 ] environ 332 000 fois celui de la Terre, soit presque exactement 2 x 1027 tonnes. Quelle que soit la planète utilisée, nous obtenons exactement le même poids pour le Soleil. Cela nous conforte non seulement dans notre résultat, mais apporte aussi une confirmation éclatante de la véracité de la loi de gravitation de Newton. En effet, si cette loi était inexacte ou fausse, les différentes planètes ne raconteraient pas toutes exactement la même histoire quant au poids du Soleil. Einstein a récemment démontré que cette loi n’est pas absolument exacte, mais que cette inexactitude est inappréciable, sauf pour la planète la plus proche, Mercure, et même ici, elle est si minime que nous n’avons pas à nous en préoccuper pour le présent propos.

De même que nous pouvons peser le Soleil et la Terre en étudiant le mouvement d’un corps soumis à leur attraction gravitationnelle — ou « dans leurs champs gravitationnels », comme dirait le mathématicien —, nous pouvons peser tout autre corps qui, par son attraction gravitationnelle, maintient un second petit corps en mouvement autour de lui. Les mouvements des satellites de Jupiter permettent de peser Jupiter ; son poids est estimé à environ 1,92 x 1024 tonnes, soit 317 fois celui de la Terre, mais seulement 1/1047 de celui du Soleil. De même, le poids de Saturne est estimé à 5,71 x 1023 tonnes, soit environ 94,9 fois celui de la Terre.
Peser les étoiles. Nous en arrivons maintenant à une application frappante des principes qui viennent d’être expliqués : lorsque nous observons deux étoiles dans le ciel décrivant des orbites l’une autour de l’autre, nous pouvons les peser à partir de l’étude de leurs orbites. En général, le problème n’est pas aussi simple que ceux que nous venons d’aborder. Pour le traiter correctement, nous devons une fois de plus nous appuyer sur les travaux mathématiques de Newton.
Nous avons vu qu’un projectile tiré horizontalement à une vitesse de 7,90 kilomètres par seconde décrirait [ p. 46 ] des cercles infinis autour de la Terre. Que se passerait-il s’il était tiré dans une autre direction et à une autre vitesse ?
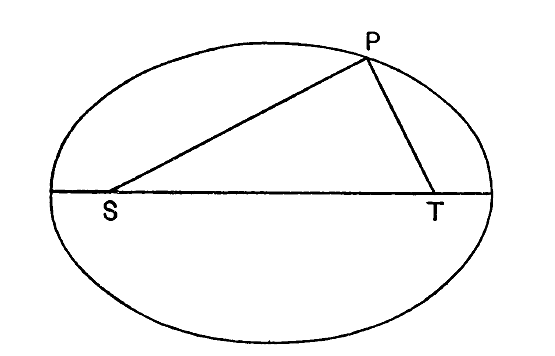
La réponse fut apportée par Newton. Il démontra que lorsqu’un petit corps est autorisé à se déplacer librement sous l’attraction gravitationnelle d’un grand corps, il s’emballe complètement si sa vitesse dépasse une certaine valeur critique, auquel cas son orbite est une courbe appelée hyperbole. Mais si sa vitesse est inférieure à cette valeur critique, son orbite sera toujours une ellipse — une sorte de cercle étiré ou de courbe ovale[3] (fig. 4, p. 47). Auparavant, Kepler avait découvert que les trajectoires réelles des planètes autour du Soleil n’étaient pas des cercles exacts, mais des ellipses, bien que pour la plupart des ellipses qui ne différaient pas beaucoup des cercles ; ce sont ce que le mathématicien appelle des « ellipses de faible excentricité ». Ceci confirme encore davantage la loi de la gravitation de Newton, car il peut être prouvé que si la force de gravitation diminue dans n’importe quelle [ p. 47 ] autrement que selon la loi de Newton du carré inverse de la distance, les orbites des planètes ne seront pas elliptiques.
Lorsque l’astronome étudie les mouvements d’une étoile binaire dans le ciel, il constate généralement que les deux composantes ne se déplacent pas en cercles l’une autour de l’autre, mais en ellipses[4]. Une fois de plus, la loi de Newton est confirmée, et nous sommes en droit de supposer que les forces qui maintiennent les étoiles binaires ensemble sont les mêmes forces gravitationnelles que celles qui empêchent la Lune de s’éloigner de la Terre, ou les planètes du Soleil. L’étude de ces ellipses permet de peser les étoiles. Si l’une des masses des composantes était énormément plus lourde que l’autre, la première resterait immobile tandis que la composante, plus légère, décrirait une ellipse autour d’elle, le mouvement étant essentiellement similaire à celui d’une planète autour du Soleil. De tels cas ne sont pas observés dans les étoiles binaires réelles, car les deux composantes ont généralement des poids comparables, ce qui complique la question. Il n’est pas nécessaire d’entrer ici dans les détails mathématiques. Il suffit de dire qu’aucune des deux étoiles ne reste immobile ; les deux composantes décrivent des ellipses de tailles différentes, et à partir d’une étude de ces deux ellipses, les poids des deux composantes peuvent être déterminés.
Le tableau suivant montre le résultat de la pesée des quatre systèmes binaires les plus proches du soleil de cette manière, le poids du soleil étant pris comme unité :
| Étoile | Distance en années-lumière du Soleil | Poids des composants en fonction du poids du Soleil | Luminosité (voir p. 49) |
|---|---|---|---|
| Centaure A | 4.31 | 1.14 | 1.12 |
| « B | 0,97 | 0,32 | |
| Sirius A | 8,65 | 2,45 | 26,3 |
| « B | 0,85 | 0,0026 | |
| Procyon A | 10,5 | 1,24 | 5,5 |
| « B | 0,39 | 0,00003 | |
| Kruger 60 A | 12,7 | 0,25 | 0,0026 |
| « B | 0,20 | 0,0007 |
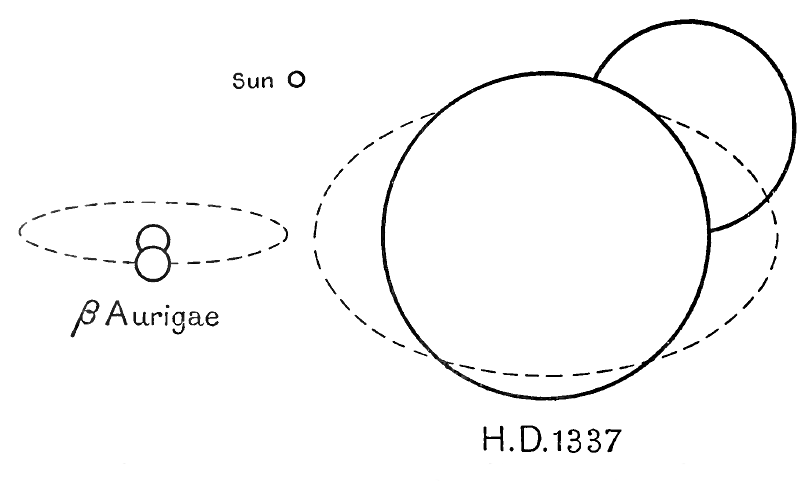
Nous voyons que les poids de ces étoiles ne diffèrent pas beaucoup de celui du Soleil, bien que naturellement l’ensemble de l’espace offre une portée plus grande que les quatre étoiles de notre tableau qui se trouvent proches du Soleil. Mais même dans l’ensemble de l’espace, aucune étoile dont le poids est connu avec précision n’a un poids inférieur à Kruger 60 B, bien qu’à l’autre extrémité de l’échelle, il existe de nombreuses étoiles dont le poids est bien plus élevé que celui de notre tableau. Parmi les étoiles dont le poids est connu avec une assez bonne précision, l’étoile HD 1337 (l’étoile de Pearce) est la plus lourde, ses deux composantes étant respectivement 36,3 et 33,8 fois plus lourdes que le Soleil. L’étoile BD 6° 1309 de Plaskett est certainement plus lourde encore, ses composantes pesant au moins 75 et 63 fois plus que le Soleil, et probablement plus ; Les poids exacts ne sont pas connus (voir p. 55 ci-dessous). Le système 27 Canis Majoris est constitué de quatre étoiles, dont le poids combiné, selon les données actuellement disponibles, semble être au moins 940 fois celui du Soleil, mais nous pouvons faire preuve d’une certaine prudence avant d’accepter un chiffre si éloigné de la fourchette habituelle des poids stellaires.
L’étoile constituante moyenne dans le tableau très court ci-dessus a 0,94 fois le poids du soleil, de sorte que notre soleil semble avoir un poids bien supérieur à la moyenne, et cela est confirmé par une étude plus approfondie des poids stellaires.
On aurait pu s’attendre a priori à ce que les étoiles possèdent toutes sortes de poids, car rien ne s’oppose à ce qu’il existe des étoiles dont le poids est des millions de fois supérieur à celui du Soleil, ou encore dont le poids est seulement égal à celui de la Terre, voire inférieur. En réalité, les poids des étoiles sont généralement assez égaux, très peu d’entre elles ayant un poids très différent de celui du Soleil. Cela semble indiquer qu’une étoile est une espèce définie de produit astronomique, et non un simple fragment aléatoire de matière lumineuse.
Luminosité. La dernière colonne du tableau, p. 48, donne les « luminosités » des étoiles, c’est-à-dire leur puissance en bougies, celle du Soleil étant prise comme unité. Par exemple, l’entrée 26,3 pour Sirius signifie que Sirius, considéré comme un phare dans l’espace, a 26,3 fois la puissance en bougies du Soleil. Les luminosités des étoiles présentent une portée considérablement plus grande que leurs poids. D’une manière générale, les étoiles les plus lourdes sont les plus lumineuses, comme on peut naturellement s’y attendre, mais leur luminosité est hors de proportion avec leur poids. La composante la plus lourde de Sirius n’a que 2,9 [ p. 50 ] fois le poids de la composante la plus légère, mais 10 000 fois sa luminosité. De même, dans le système de Procyon, la composante la plus lourde a un poids 3,2 fois supérieur, mais une luminosité 180 000 fois supérieure, à celle de la composante la plus légère. Il semble qu’il s’agisse d’une loi quasi universelle selon laquelle la puissance d’une bougie par tonne est bien supérieure dans les étoiles lourdes que dans les étoiles lumineuses. C’est l’un des faits centraux et, à première vue, l’un des plus déroutants de l’astronomie physique : il est si fondamental et si omniprésent qu’aucune conception du mécanisme stellaire ne peut être acceptée si elle ne parvient pas à l’expliquer.
Vitesses spectroscopiques. Lorsque la distance d’une étoile est connue, son mouvement dans le ciel nous indique sa vitesse dans une direction perpendiculaire à la ligne le long de laquelle nous l’observons – c’est-à-dire à travers la ligne de visée – mais ne fournit aucun moyen de connaître sa vitesse le long de cette ligne. Nous ne pouvons pas voir le mouvement d’un corps qui vient droit vers nous, et une étoile se déplaçant à un million de kilomètres par seconde dans une direction exactement le long de la ligne de visée semblerait pourtant immobile dans le ciel. Pour évaluer les vitesses le long de la ligne de visée, l’astronome fait appel au spectroscope.
Toute lumière est un mélange de lumières de différentes couleurs, et tout comme Newton, avec son célèbre prisme, a analysé la lumière du Soleil en toutes les couleurs de l’arc-en-ciel, le spectroscope analyse la lumière d’une étoile, ou de toute autre source, en ses différentes couleurs constitutives. L’instrument répartit la lumière analysée en une bande lumineuse de couleur graduée en continu, appelée « spectre ». Dans ce spectre, les couleurs sont les mêmes et se trouvent disposées dans le même ordre que dans l’arc-en-ciel, allant du violet au rouge en passant par le vert et l’orange. Il y a une raison physique à cela. Nous verrons plus loin (p. 114) que la lumière [ p. 51 ] est constitué de trains d’ondes — comme les ondulations que le vent fait sur un étang — et que les différentes couleurs de lumière résultent d’ondes de différentes longueurs, la lumière rouge étant produite par les ondes les plus longues et la lumière violette par les plus courtes. Les couleurs du spectre apparaissent dans l’ordre de leurs longueurs d’onde, de la plus longue (rouge) à la plus courte (violet). Dans le spectre stellaire typique, certaines courtes plages de couleurs ou de longueurs d’onde sont généralement absentes, pour des raisons que nous examinerons plus loin (p. 126), de sorte que le spectre semble traversé par un certain nombre de lignes ou de bandes sombres, formant ainsi un motif plutôt qu’une gradation continue de couleurs. Des exemples de spectres stellaires sont présentés dans la Planche VIII.

Il est souvent pratique de classer les étoiles selon le type de spectre qu’elles émettent. On sait maintenant que le spectre d’une étoile dépend principalement de la température de sa surface. Par conséquent, les spectres stellaires peuvent généralement être disposés en une seule séquence continue, et leur classification habituelle se fait par une suite de lettres : O, B, A, F, G, K, M, subdivisées en décimales. La température diminue au fur et à mesure que l’on avance dans la séquence, de sorte que les étoiles de type O ont les températures de surface les plus élevées et les étoiles de type M les plus basses. Les types spectraux sont indiqués à gauche dans la Planche VIII.
Lorsqu’on analyse la lumière reçue d’une étoile au spectroscope, on constate que le motif de raies ou de bandes est décalé dans un sens ou dans l’autre. Si le décalage se fait vers le rouge, la lumière émise par l’étoile nous parvient plus rouge que ce qu’elle devrait être normalement. Or, comme la lumière rouge a la plus grande longueur d’onde, chaque onde lumineuse est plus longue – plus étirée – que la normale. On en conclut que l’étoile s’éloigne de nous [ p. 52 ]. De même, si le motif spectral est décalé vers le violet, on sait que l’étoile doit se rapprocher de nous. Le décalage d’un spectre résultant du mouvement du corps qui l’émet est généralement appelé « effet Doppler ». À partir de son intensité, on peut calculer la vitesse réelle d’une étoile le long de la ligne de visée, et le calcul est étonnamment simple. Si chaque ligne ou bande d’un spectre représente une longueur d’onde d’un centième de pour cent plus longue que celle qui lui est habituellement associée, alors la vitesse de récession de l’étoile est d’un centième de pour cent de la vitesse de la lumière, soit 18,6 miles par seconde — et de même pour tous les autres déplacements.
Binaires spectroscopiques.** Comme les deux composantes d’un système binaire se déplacent généralement à des vitesses différentes, le spectre normal d’un système binaire est constitué de deux spectres distincts superposés, chacun présentant des décalages différents correspondant aux vitesses des deux composantes. À partir des orbites observées des deux composantes d’un système binaire, un astronome pourrait calculer les vitesses auxquelles ces composantes se déplaceraient dans la direction de la ligne de visée, et pourrait alors prédire dans quelle mesure les deux spectres devraient être déplacés si la lumière du système était analysée dans un spectroscope ; le spectroscope confirmerait bien sûr sa prédiction.
Il est plus instructif d’imaginer le processus inverse. Supposons qu’en analysant la lumière d’une étoile, l’astronome obtienne un spectre composite dans lequel deux spectres distincts se décalent rythmiquement en avant et en arrière par rapport à leur position normale. La présence de deux spectres lui indique qu’il s’agit d’un système binaire ; si le décalage rythmique se répète tous les deux ans, il sait que son orbite prend deux [ p. 53 ] ans. Il étudie l’étoile par vision directe et découvre qu’il s’agit d’un système binaire dans lequel les constituants tournent l’un autour de l’autre tous les deux ans.
Il examine un autre spectre et constate qu’il se déplace rythmiquement tous les deux jours. En regardant directement cette étoile, il ne voit qu’un seul point lumineux. Il doit bien sûr y avoir deux étoiles, mais le simple fait qu’elles se tournent l’une autour de l’autre en aussi peu de temps que deux jours prouve qu’elles doivent être très proches l’une de l’autre, et il n’y a pas lieu de s’étonner que son télescope n’ait pas réussi à séparer l’image en deux points lumineux distincts. Les systèmes de ce type, que le spectroscope montre comme binaires, mais que le télescope montre généralement comme un seul point lumineux, sont appelés « binaires spectroscopiques ». Plus d’un millier de ces systèmes sont connus.
Si l’astronome tente de construire l’orbite d’un tel système à partir des seules observations spectroscopiques, il se trouve en difficulté. Ses observations ne lui indiquent que les vitesses le long de la ligne de visée, et celles-ci dépendent à la fois de la vitesse réelle et du degré de raccourcissement ; la même vitesse peut provenir soit d’une grande orbite dans un plan presque perpendiculaire à la ligne de visée, soit d’une petite orbite très raccourcie. Il est impossible de calculer l’orbite réelle ou le poids des étoiles à partir de la seule observation spectroscopique.
[ p. 54 ]
Binaires à éclipses. Il existe une exception. Supposons que la lumière d’une étoile diminue à intervalles réguliers, puis revienne à son intensité initiale. L’interprétation évidente de cette diminution de lumière est qu’une composante du système éclipse l’autre, ce qui ne peut se produire que si l’orbite est tellement raccourcie que son plan passe par la Terre, ou du moins très près de celle-ci. Dans ce cas, il est possible de reconstituer l’orbite entière et de calculer ainsi les poids des deux composantes. De plus, la durée des éclipses nous renseigne sur les tailles réelles des deux composantes, ce qui permet de dresser un tableau complet du système. La figure 6 présente les dimensions et les orbites de deux binaires à éclipses typiques ; elles sont dessinées à la même échelle, celle-ci étant indiquée par le petit cercle représentant le Soleil.
Lorsqu’aucune éclipse ne se produit dans une binaire spectroscopique, nous ne savons pas quel degré de raccourcissement prendre en compte, mais nous pouvons obtenir une idée générale des poids des composantes en supposant un degré moyen de raccourcissement. Si nous supposons différents degrés de raccourcissement à tour de rôle, nous constaterons que les poids calculés sont les plus faibles lorsque le plan de l’orbite est supposé passer par la Terre, c’est-à-dire lorsque les orbites sont calculées comme si le système était à éclipses. Ainsi, bien que nous ne puissions pas découvrir les poids réels des composantes d’une binaire sans éclipses, nous pouvons toujours établir des limites au-dessus desquelles elles doivent se situer, à savoir les poids calculés comme si le système était à éclipses. De cette façon, nous savons que les deux composantes de l’étoile de Plaskett doivent avoir plus de 75 et 63 fois le poids du Soleil.
¶ Étoiles variables
La majorité des étoiles brillent d’une lumière parfaitement stable, ce qui permet de dire qu’une étoile a une puissance en bougies. Le Soleil, par exemple, émet une lumière de 3,23 x 1027 bougies.
Il existe pourtant des classes d’étoiles exceptionnelles dont la lumière oscille de haut en bas. Chez certaines, comme dans les binaires à éclipses décrites précédemment, les fluctuations lumineuses sont assez régulières, se répétant avec une telle précision que les étoiles pourraient bien servir de chronomètres. Chez d’autres, les fluctuations, bien que non parfaitement régulières, le sont presque, tandis que d’autres encore semblent actuellement totalement irrégulières, même si leurs variations seront sans doute maîtrisées en temps voulu. Pour notre discussion actuelle, les différents types de variables irrégulières n’ont pas une grande importance.
Variables céphéides. Les étoiles vraiment intéressantes sont celles d’une certaine classe de variables régulières, généralement [ p. 56 ] appelées « variables céphéides », d’après leur prototype δ Céphées. La nature physique de ces étoiles et le mécanisme de leurs fluctuations lumineuses sont encore loin d’être compris ; des théories concurrentes sont en cours d’élaboration, dont nous n’avons pas besoin de discuter à ce stade (voir p. 223 ci-dessous).
Quel que soit leur mécanisme, l’observation montre que ces étoiles possèdent une propriété bien définie, d’une valeur capitale. Ceci étant, nous pouvons l’accepter avec gratitude sans nous soucier de son pourquoi et de son pourquoi. Les fluctuations lumineuses parfaitement régulières des binaires à éclipses les rendraient idéales pour l’observation du temps, même si nous ignorions le mécanisme qui les sous-tend. De même, les fluctuations des variables Céphéides possèdent une qualité qui les rend précieuses comme indicateurs pour observer les régions lointaines de l’univers. En résumé, cette propriété permet de déduire la luminosité intrinsèque de ces étoiles, et donc leurs distances, à partir des fluctuations lumineuses observées.
Les fluctuations de lumière sont si caractéristiques qu’elles facilitent la détection des étoiles. On observe une augmentation rapide de la luminosité, suivie d’une lente diminution progressive ; puis à nouveau la même augmentation rapide et la même lente diminution que précédemment. C’est comme si quelqu’un jetait des brassées de combustible sur un feu de joie à intervalles parfaitement réguliers.
Une autre classe d’étoiles variables, généralement appelées « variables à longue période », présente des fluctuations lumineuses assez similaires, mais les deux classes se distinguent facilement par leurs périodes de fluctuation lumineuse très différentes. La variable Céphéide accomplit son cycle en quelques heures, quelques jours ou quelques semaines, mais jamais plus d’un mois environ, tandis que la variable à longue période nécessite généralement environ un an.
[ p. 57 ]
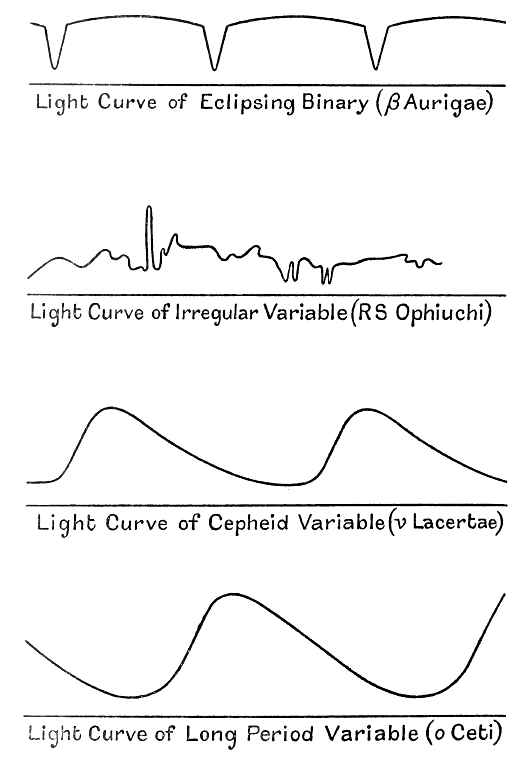
Fig. 7 montre les courbes de lumière d’étoiles variables typiques des différentes classes. Dans chaque diagramme, la progression du temps est représentée par un mouvement sur la page, de gauche à droite ; plus la courbe fluctuante est élevée au-dessus de la ligne horizontale à un instant donné, plus l’étoile est brillante à cet instant.
Près de la frontière du système galactique se trouve un amas d’étoiles connu sous le nom de Petit Nuage de Magellan (Planche XXI, p. 214), dans lequel les variables Céphéides sont présentes en grande abondance. En 1912, Mlle Leavitt de Harvard a découvert que la lumière des Céphéides les plus brillantes de ce nuage fluctuait plus lentement que celle des plus faibles. Le facteur responsable de l’augmentation et de la diminution de la luminosité stellaire agissait plus rapidement pour les lumières faibles que pour les lumières brillantes. La luminosité apparente de plusieurs Céphéides à différentes distances ne dépendrait bien sûr qu’en partie de leur luminosité intrinsèque ou de leur puissance en bougies, mais les étoiles du Nuage de Magellan sont toutes, à peu près, à la même distance de la Terre. Ainsi, les différences de luminosité apparente des étoiles de ce nuage doivent représenter de réelles différences de luminosité intrinsèque, et la découverte de Mlle Leavitt pourrait s’exprimer ainsi : la période de fluctuation lumineuse d’une Céphéide dépend de sa puissance en bougies. Bien que cela n’ait été prouvé que pour les Céphéides du Nuage de Magellan, cela doit être vrai pour toutes les Céphéides, où qu’elles se trouvent, car il est inconcevable que nous puissions ralentir ou accélérer la fluctuation lumineuse d’une étoile simplement en modifiant sa distance – en nous éloignant d’elle, en réalité.
Le professeur Hertzsprung de Leyde et le Dr Shapley, alors à l’observatoire du mont Wilson, ont rapidement saisi les implications de cette découverte. Si deux Céphéides A et B, situées dans des parties différentes du ciel, fluctuent avec la même rapidité, alors leurs puissances intrinsèques doivent être égales. Ainsi, toute différence dans leur luminosité apparente doit être imputable à une différence de distance par rapport à nous. Si A paraît cent fois plus brillante que B, alors B doit être à dix fois la distance de A. De la même manière, une troisième Céphéide C peut se trouver à dix fois la distance de B. Nous savons maintenant que C est cent fois plus éloignée que A. Et si D peut être trouvée dix fois plus éloignée que C, nous savons que D est mille fois plus éloignée que A. Nous pouvons donc continuer à construire et à étendre sans cesse notre règle de mesure ; il n’y a pas de limite jusqu’à ce que nous atteignions des distances si grandes que même les variables Céphéides, qui sont des étoiles exceptionnellement brillantes, disparaissent dans l’invisibilité.
Jusqu’ici, nous n’avons considéré que les distances comparatives des Céphéides. Les distances absolues de nombreuses Céphéides les plus proches ont cependant été déterminées par la méthode parallactique déjà expliquée, c’est-à-dire en mesurant leur mouvement apparent dans le ciel, résultant du mouvement de la Terre autour du Soleil. En prenant n’importe laquelle de ces étoiles comme Céphéide A d’origine, nous pouvons passer continuellement d’une Céphéide à l’autre et ainsi calculer les distances absolues de toutes les Céphéides variables dans le ciel.
De cette façon, la relation observée entre la période de fluctuation et la luminosité des variables céphéides — communément appelée « loi période-luminosité » — peut être utilisée pour fournir une échelle permettant de déduire directement la luminosité absolue, ou la puissance en bougies, d’une céphéide de la période observée de ses fluctuations lumineuses. Les variables céphéides peuvent être considérées comme des phares installés dans des régions éloignées de l’univers. Nous pouvons les reconnaître, tout comme un marin [ p. 60 ] reconnaît les phares, à la qualité de leur lumière. Nous pouvons déduire leur puissance en bougies de la période de leurs fluctuations lumineuses observées aussi facilement qu’un marin pourrait déduire la puissance en bougies d’un phare sur une carte de l’Amirauté. La luminosité apparente de la céphéide nous renseigne sur sa distance par rapport à nous[5].
On ne saurait surestimer l’importance de tout cela pour la science astronomique moderne. Cela signifie qu’une méthode a été trouvée pour étudier, sinon l’univers entier, du moins les parties de celui-ci où les variables céphéides sont visibles. En réalité, cette dernière réserve est sans importance, car les variables céphéides sont très librement dispersées dans l’espace. Naturellement, cette méthode est particulièrement utile pour l’exploration des régions les plus lointaines de l’univers ; elle y remporte un succès triomphal là où d’autres méthodes échouent complètement. La méthode parallactique commence à échouer lorsque nous tentons de sonder des distances de plus d’une centaine d’années-lumière. La trajectoire apparente dans le ciel, décrite par une étoile à cette distance, en raison du mouvement de la Terre autour du Soleil, est de la taille d’une tête d’épingle à trois kilomètres de distance. Malgré tous leurs perfectionnements, les instruments modernes peinent à détecter un mouvement aussi faible, et il est pratiquement impossible de le mesurer avec précision. La loi « période-luminosité » mesure les distances des objets jusqu’à un million d’années-lumière, avec un pourcentage d’erreur plus faible que celui auquel on peut s’attendre dans les mesures parallactiques des étoiles situées à seulement cent années-lumière.
¶ Espace sonore
Ceci est loin d’épuiser la liste des méthodes modernes d’observation de l’espace. Tout objet astronomique standard, facilement reconnaissable et émettant la même quantité de lumière où qu’il se trouve, constitue un moyen évident de mesurer les distances astronomiques. En effet, une fois la luminosité intrinsèque d’un tel objet déterminée, la distance de chaque exemplaire peut être estimée à partir de sa luminosité apparente.
Les variables céphéides de périodes assignées constituent l’exemple le plus frappant de ces objets standards, mais trois autres sont disponibles, bien que moins utiles que les céphéides. Il y a d’abord un autre type d’étoile variable, les « variables à longue période » déjà mentionnées, qui sont généralement similaires aux céphéides, si ce n’est que leur lumière fluctue beaucoup plus lentement. Ces étoiles sont intrinsèquement bien plus lumineuses que les céphéides, nombre d’entre elles étant 10 000 fois plus lumineuses que le Soleil. Elles sont donc visibles à des distances énormes et pourraient permettre de sonder des profondeurs spatiales où même les céphéides sont invisibles.
Viennent ensuite les « novae », ou nouvelles étoiles. De temps à autre, une étoile ordinaire du ciel éclate dans un éclat phénoménal, brillant peut-être mille fois plus que son éclat initial. La cause de ces violentes explosions fait encore débat, et aucune explication convaincante n’a encore été fournie. Une étude de novae relativement proches a cependant fourni des informations sur la luminosité d’une nova moyenne à son maximum d’éclat. Comme les novae apparaissent dans diverses parties du ciel, et en particulier dans les nébuleuses extragalactiques, elles fournissent un moyen approximatif de mesurer les distances stellaires et nébuleuses.
Les étoiles bleues offrent une autre méthode. Elles sont extrêmement lumineuses et leur luminosité intrinsèque varie peu. De plus, la luminosité d’une étoile donnée peut généralement être estimée assez précisément à partir de la qualité de la lumière qu’elle émet, par des méthodes qui seront expliquées plus loin. Cela permet de déterminer les distances des étoiles bleues, et donc, bien sûr, des objets astronomiques dans lesquels elles se trouvent.
Deux autres méthodes, d’un genre différent, peuvent être brièvement mentionnées. Le Dr WS Adams, directeur de l’observatoire du mont Wilson, et d’autres ont découvert que certaines particularités du spectre de certaines classes d’étoiles renseignent sur la luminosité intrinsèque de l’étoile qui les émet ; grâce à ces informations, il est facile d’estimer la distance de l’étoile par rapport à sa luminosité apparente. Cette méthode est communément appelée la méthode des parallaxes spectroscopiques.
Enfin, on a découvert que le nuage diffus de matière nébulaire qui se propage dans l’espace interstellaire (p. 30) affecte la qualité de la lumière qui le traverse, de sorte que le spectre d’une étoile donne une indication de la quantité de nuage à travers lequel la lumière de l’étoile a [ p. 63 ] voyagé, ce qui fournit à nouveau un moyen approximatif d’estimer les distances à l’intérieur du système galactique.

Amas globulaires. La loi de luminosité des Céphéides fut utilisée pour la première fois par Hertzsprung pour estimer la distance du Petit Nuage de Magellan, dont l’étude avait été à l’origine de la découverte originale de cette loi. Shapley l’utilisa ensuite pour déterminer les distances des mystérieux groupes d’étoiles appelés « amas globulaires ». Un exemple typique est présenté dans la Planche IX. Une centaine de ces amas sont connus et ils se ressemblent tous assez bien, à l’exception de différences de taille apparente. Même ces dernières peuvent être attribuées principalement à des différences de distance, de sorte que les amas globulaires sont probablement des objets presque identiques, et la Planche IX pourrait presque être considérée comme une représentation de l’un d’entre eux. Les variables Céphéides abondent dans chacun d’eux.
Shapley a trouvé que l’amas globulaire le plus proche, γ du Centaure, se trouvait à environ 22 000 années-lumière, le plus éloigné, NGC 7006, étant environ dix fois plus éloigné, à 220 000 années-lumière. À de telles distances, la méthode parallactique de mesure des distances serait évidemment vouée à l’échec. L’orbite parallactique d’une étoile à 220 000 années-lumière est à peu près de la taille d’une tête d’épingle tenue à 6 400 kilomètres de distance ; aucun télescope sur Terre ne pourrait détecter, et encore moins mesurer, une telle orbite.
Le simple chiffre de 220 000 années-lumière ne peut donner qu’une faible idée de la distance qui nous sépare de cet amas d’étoiles des plus éloignés. On peut mieux l’appréhender en réfléchissant au fait que la lumière qui nous permet de voir cet amas a commencé son long voyage depuis lui jusqu’à nous à peu près à l’époque où l’homme primitif est apparu sur Terre. À travers l’enfance, la jeunesse et la vieillesse d’innombrables générations d’hommes, à travers les longs âges préhistoriques, à travers la lente ascension de la civilisation et à travers toute la période que l’histoire enregistre, à travers l’ascension et la chute des dynasties et des empires, cette lumière a parcouru sa course régulière, parcourant 300 000 kilomètres par seconde, et elle nous atteint à peine aujourd’hui. Et pourtant, cette immense étendue d’espace ne nous conduit pas aux confins de l’univers ; nous allons maintenant voir qu’en toute probabilité, elle nous a à peine conduits aux confins du système galactique.
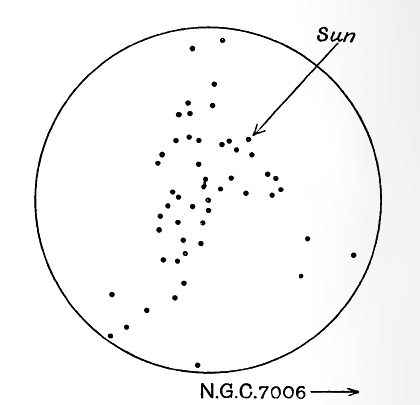
Shapley a cartographié le système complet des amas globulaires et a découvert qu’ils occupent une région oblongue, située de part et d’autre du plan de la Voie lactée. Son plus grand diamètre, d’environ 250 000 années-lumière, se situe dans ce plan, et ses deux diamètres transversaux sont considérablement plus courts. Le Soleil est plus proche du bord de cette région oblongue que de son centre, ce qui explique pourquoi tous les amas globulaires apparaissent dans une moitié du ciel, comme Hinks l’a observé pour la première fois en 1911.
[ p. 65 ]
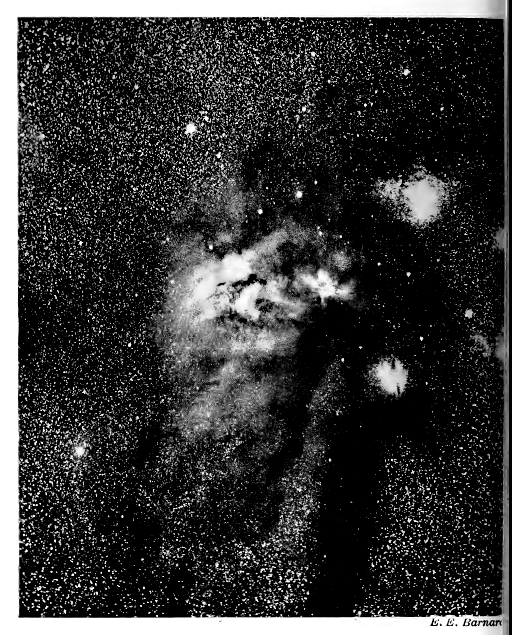
La disposition générale est illustrée dans la fig. 8. La page du livre représente le plan de la Voie lactée, les différents points représentant les points de ce plan les plus proches des différents amas. Le diagramme présente ainsi le système d’amas globulaires tel qu’il apparaîtrait à un observateur spatial observant le plan galactique de près. Tous les amas globulaires, à l’exception de NGC 7006, se situent dans un cercle d’environ 125 000 années-lumière de rayon, dont le centre se trouve à environ 50 000 années-lumière du Soleil.
¶ L’agencement du système galactique.
Bien que cette question ait longtemps fait l’objet d’une vive controverse, il apparaît désormais clairement que la région de l’espace délimitée par ces amas globulaires coïncide approximativement avec celle occupée par le système galactique lui-même. Herschel et Kapteyn semblent s’être trompés en supposant que le centre du système galactique se trouvait au voisinage du Soleil ; de nombreuses preuves indiquent qu’il se situe dans un nuage d’étoiles massif, dans les constellations d’Ophiuchus et du Scorpion. Le Dr Shapley et Mlle Swope, de l’observatoire de Harvard, ont récemment déterminé la distance de ce nuage d’étoiles au Soleil à 47 000 années-lumière, ce qui le place presque exactement au centre du système d’amas globulaires, comme le montre la fig. 8. Il existe ce que Shapley décrit comme un « système local » d’étoiles assez brillantes entourant le Soleil, et l’erreur consistant à l’identifier au système galactique principal a apparemment été en grande partie responsable de la confusion qui a jusqu’ici entaché le problème de l’architecture de la galaxie. Ce système local a la même forme aplatie que le système principal, mais il ne se situe pas exactement dans le plan de la Voie lactée, étant incliné d’environ [ p. 66 ] 12 degrés par rapport à celui-ci. Le Soleil semble se trouver très près du plan central du système ; des déterminations récentes le situent à environ 100 années-lumière au nord de ce plan. La Fig. 9 montre une coupe transversale du système, telle qu’on l’imagine aujourd’hui.
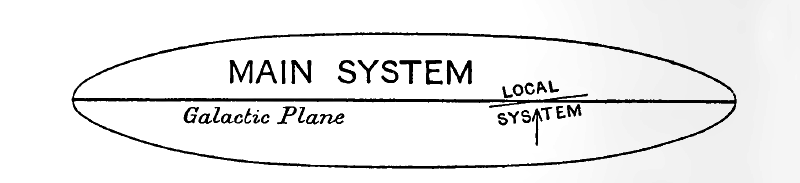
Nous avons déjà comparé la forme du système galactique à celle d’une roue. Il ne pourrait évidemment pas conserver cette forme si les étoiles qui le composent étaient immobiles dans l’espace. En effet, l’attraction gravitationnelle des étoiles intérieures entraînerait la chute des étoiles extérieures – la jante de la roue – vers l’intérieur, et le système finirait par n’être qu’un amas confus d’étoiles quelque part à proximité du moyeu de la roue. En 1913, Henri Poincaré, professeur de mathématiques à la Sorbonne, suggéra que la « roue » galactique pourrait échapper à ce sort si elle était en rotation. De même que le mouvement de la Terre l’empêche de tomber sur le Soleil et que le mouvement de la Lune l’empêche de tomber sur la Terre, de même, suggérait Poincaré, les étoiles qui forment la jante de la roue pourraient être empêchées de tomber sur le moyeu par un mouvement de rotation de la roue entière. Un calcul approximatif suggérait qu’il serait nécessaire que la roue tourne à la vitesse d’une révolution complète tous les 500 millions d’années environ.
Naturellement, il n’est pas simple de détecter une rotation aussi lente. On a d’abord soupçonné qu’elle se produisait de la manière suivante. Nous savons que lorsqu’une toupie ou un gyroscope est mis en rotation rapide, une force considérable est nécessaire pour la faire tourner dans l’espace. C’est le principe du compas gyroscopique utilisé pour diriger les navires. Un gyroscope, sorte de grande toupie en acier, est mis en rotation, ses deux extrémités pivotant dans un cadre oscillant. Quelle que soit la direction du navire, le mouvement du gyroscope maintient le cadre pointé dans la même direction, et grâce à cette direction fixe, le navire maintient son cap. Or, le système solaire possède de nombreuses propriétés d’une immense toupie, les révolutions des planètes correspondant à la rotation de la toupie. Comme aucune torsion n’est imprimée à cette « toupie » de l’extérieur, son axe de rotation doit toujours pointer dans la même direction, constituant ainsi une sorte de « boussole gyroscopique » pour nous orienter dans l’espace.
En 1913, Charlier crut avoir découvert que cette « boussole gyroscopique » tournait sur elle-même devant la Voie lactée, un lointain arrière-plan, à la vitesse d’une rotation complète tous les 370 millions d’années, une période que les mesures ultérieures portèrent à 530 millions d’années. Eddington suggéra alors que c’était peut-être l’arrière-plan plutôt que la boussole gyroscopique qui tournait, la Voie lactée tournant en réalité comme l’imaginait Poincaré, et à peu près à la vitesse calculée par Poincaré.
Des recherches récentes menées par Oort, Plaskett, Lindblad et d’autres prouvent sans l’ombre d’un doute qu’une telle rotation se produit réellement, bien qu’elle ne soit pas du type simple « roue de charrette » dont nous avons parlé jusqu’à présent. Dans le système solaire, les planètes les plus intérieures se déplacent plus rapidement que les plus extérieures : elles doivent nécessairement le faire si le mouvement de chaque planète doit contrecarrer l’attraction du Soleil. De même, si le mouvement de rotation de la galaxie [ p. 68 ] doit contrecarrer l’attraction gravitationnelle de ses étoiles les plus intérieures, ses parties intérieures doivent tourner plus rapidement que ses plus extérieures. Ainsi, le Soleil devrait dépasser les étoiles qui se trouvent à l’extérieur de lui sur la roue galactique, tout en étant lui-même dépassé par celles qui se trouvent à l’intérieur. Un tel mouvement de dépassement est assez facile à détecter. Une analyse minutieuse des mouvements stellaires observés a révélé un tel mouvement, montrant que la galaxie dans son ensemble est en rotation exactement de la manière qui vient d’être décrite, les parties intérieures tournant plus rapidement.
Le moyeu de cette roue gigantesque se trouve presque exactement dans la direction que Shapley a assignée au centre de la galaxie à partir de son étude des amas globulaires. Sa distance au Soleil, encore difficile à déterminer avec une grande précision, est probablement d’environ 37 000 années-lumière. Dans les limites de la précision actuellement réalisable, cela place le centre de la roue galactique au centre du système d’amas globulaires (voir fig. 8, p. 64). À proximité du Soleil, la roue galactique effectue une révolution complète en environ 230 millions d’années, ce qui confère aux étoiles proches du Soleil un mouvement spatial à une vitesse de près de 320 kilomètres par seconde, résultant de la seule rotation de la galaxie.
Grâce à ces données, il est possible de peser les étoiles du système galactique en masse. Les étoiles individuelles, éloignées du centre du système galactique, doivent décrire des orbites sous l’effet de l’attraction gravitationnelle du système dans son ensemble, attraction qui empêche les étoiles de se disperser dans l’espace et maintient ainsi le système galactique en vie. L’ensemble de ces mouvements orbitaux produit la rotation générale de la galaxie que nous venons d’examiner. Et d’après les chiffres mentionnés, on peut calculer que le poids total [ p. 69 ] de la matière à l’intérieur de l’orbite du Soleil doit être d’environ 240 000 millions de soleils. Une partie de ce poids peut bien sûr provenir de la poussière ou du gaz interstellaire. Néanmoins, comme l’étoile moyenne pèse considérablement moins que le Soleil, le nombre total d’étoiles dans le système galactique pourrait bien être de l’ordre de 400 000 millions. Cette estimation inclut bien sûr toutes les étoiles, sombres comme lumineuses, mais il y a des raisons de croire que le nombre d’étoiles sombres est relativement faible (voir p. 269 ci-dessous).
D’autres estimations du nombre d’étoiles dans la galaxie ont été faites, généralement inférieures aux précédentes. Deux estimations de Lindblad, par exemple, donnent le poids total de la galaxie à respectivement 110 000 et 180 000 millions de soleils.
Nous sommes à nouveau confrontés à la difficulté de visualiser des nombres aussi importants. Avec une vue parfaite, par une nuit claire et sans lune, nous pouvons voir environ 3 000 étoiles. Imaginez que chacune de ces 3 000 étoiles se déploie dans un ciel entier rempli de 3 000 nouvelles étoiles, et nous en sommes à 9 millions, ce qui ne représente encore que le nombre visible dans un télescope de 12,7 cm d’ouverture. Nous ne pouvons probablement pas demander à notre imagination de nous jouer le même tour une seconde fois, mais si nous pouvons la persuader de le faire, et si nous pouvons imaginer que chacune de ces 9 millions d’étoiles génère à nouveau un ciel entier rempli d’étoiles, nous n’avons toujours que 27 000 millions d’étoiles à notre portée – un nombre bien inférieur à toute estimation admissible du nombre total d’étoiles du système galactique. Ou encore, remarquons que le nombre d’étoiles photographiquement visibles dans un télescope de 254 cm, soit 1 500 millions, est à peu près égal au nombre d’hommes, de femmes et d’enfants sur la planète. Chaque habitant de la Terre — chaque [ p. 70 ] homme, femme et enfant vivant sur les cinq continents ou voyageant sur les sept mers — peut être autorisé à choisir sa propre étoile particulière, et peut ensuite répéter le processus des dizaines, et plus probablement des centaines, de fois sans sortir du système galactique.
Après cela, nous pouvons encore explorer le système galactique et découvrir toujours plus d’étoiles. Le système galactique, avec ses centaines de millions d’étoiles, ne contient pas plus toutes les étoiles de l’espace qu’une seule maison ne contient tous les habitants de la Grande-Bretagne. Il existe des millions d’autres maisons et des millions d’autres familles d’étoiles.
Les nébuleuses extragalactiques. Nous avons déjà parlé des objets nébuleux de faible intensité qu’Herschel a décrits, de manière quelque peu conjecturale, comme des « univers-îles ». Ce sont les autres maisons dans lesquelles se trouvent d’autres familles d’étoiles. Les télescopes modernes les plus puissants montrent qu’ils sont constitués, au moins en partie, d’énormes nuages d’étoiles. De même qu’un microscope puissant montre qu’une bouffée de fumée de cigarette, malgré son apparence de continuité, est constituée d’un nuage de particules minuscules mais bien distinctes, de même un télescope moderne puissant décompose la lumière provenant des régions extérieures de ces nébuleuses en points lumineux distincts ; la nébuleuse se résout en un nuage de particules brillantes, tout comme la Voie lactée l’était dans le minuscule télescope de Galilée il y a trois siècles. Planche XI en montre un exemple ; Elle représente un agrandissement d’une petite zone dans le coin supérieur gauche de la Grande Nébuleuse M 31 d’Andromède, déjà représentée dans la Planche IV (p. 30), et la résolution en taches lumineuses distinctes est indéniable. Nous savons que certaines au moins de ces taches lumineuses sont des étoiles, car nous les reconnaissons comme des variables Céphéides, leur lumière montrant les fluctuations caractéristiques indéniables des variables Céphéides familières plus proches. Les autres particules brillantes sont d’une luminosité comparable et présentent une gamme de luminosité supérieure et inférieure à celle des Céphéides, ce qui est nécessaire pour nous permettre de supposer qu’il s’agit d’étoiles ordinaires.


À partir des périodes de fluctuation observées de leurs variables Céphéides, en combinaison avec les autres méthodes précédemment expliquées, le Dr Hubble de l’Observatoire du Mont Wilson a récemment découvert que même la plus proche de ces nébuleuses, à savoir la nébuleuse M 33 représentée sur la Planche XX (p. 213), est si lointaine que la lumière met environ 850 000 ans pour la parcourir jusqu’à nous. La Grande Nébuleuse M 31 d’Andromède (p. 30) se trouve à une distance légèrement supérieure, soit environ 900 000 années-lumière. Cela prouve amplement que ces nébuleuses se situent juste à l’extérieur du système galactique, justifiant ainsi le terme de nébuleuses « extragalactiques ».
On pourrait tenter d’estimer le nombre total d’étoiles dans ces nébuleuses en comptant celles visibles dans une petite zone moyenne sélectionnée, mais des méthodes plus précises existent. De même que nous avons supposé que les étoiles les plus éloignées du système galactique décrivent des orbites sous l’attraction gravitationnelle de la galaxie dans son ensemble, nous devons supposer que les étoiles les plus éloignées d’une nébuleuse décrivent des orbites sous l’attraction gravitationnelle de la masse principale de la nébuleuse ; les forces qui les empêchent de s’éloigner de la nébuleuse sont similaires à celles qui maintiennent la Terre en mouvement sur son orbite autour du Soleil. Si tel est le cas, nous pouvons peser les nébuleuses, exactement de la même manière que nous pesons le Soleil (p. 44) ou le système galactique (p. 69). Le Dr Hubble estime ainsi que le poids de la Grande Nébuleuse M 31 d’Andromède, représentée sur la Planche IV, doit être environ 3 500 millions de fois celui du Soleil, tandis que [ p. 72 ] la nébuleuse NGC 4594 de la Vierge, représentée sur la Planche XV (p. 204), doit avoir environ 2 000 millions de fois le poids du Soleil. En général, il semble probable que chacune des nébuleuses extragalactiques contienne suffisamment de matière pour former quelque 2 000 millions d’étoiles.
Cela ne revient pas à dire que chaque nébuleuse contient déjà 2 milliards d’étoiles. Si nombre de ces nébuleuses semblent être constituées en grande partie de nuages d’étoiles, la plupart d’entre elles contiennent également une vaste région centrale qu’aucun télescope n’a jusqu’à présent réussi à décomposer en points distincts. Par exemple, la Planche XII montre la région centrale de la Grande Nébuleuse d’Andromède agrandie au même degré que le coin supérieur gauche de la Planche XI, et celle-ci n’est manifestement pas décomposée en étoiles de la même manière que les régions extérieures de la Planche XI. L’ensemble de la nébuleuse NGC 4594 de la Vierge, représentée sur la Planche XV, refuse également d’être décomposé en étoiles distinctes. Nous trouverons plus loin (Chapitre IV) des raisons d’interpréter ces régions centrales comme des masses de gaz destinées à former des étoiles, mais qui ne l’ont pas encore fait. Nous constaterons en fait que les nébuleuses sont les berceaux des étoiles, de sorte que chaque nébuleuse est composée d’étoiles nées et d’étoiles à naître. C’est la masse totale des étoiles déjà nées et de la matière destinée à former des étoiles qui représente 2 000 millions de soleils.
Environ 2 000 000 de ces nébuleuses extragalactiques sont visibles dans le grand télescope de 100 pouces. En général, elles semblent dispersées dans l’espace avec une uniformité acceptable, leur distance moyenne étant de l’ordre de 2 000 000 d’années-lumière, bien que cette uniformité soit çà et là rompue par des nuages et des amas de nébuleuses. Par exemple, le ciel est remarquablement riche en nébuleuses dans les constellations de la Vierge et de la Chevelure de Bérénice. Ici, un nuage d’environ [ p. 73 ] 300 nébuleuses est rassemblé, selon Shapley, dans un espace dont les dimensions ne sont que de 5 à 10 fois celles du système galactique, à une distance d’environ dix millions d’années-lumière du Soleil. La même région du ciel semble également contenir trois autres nuages plus éloignés. Shapley a suggéré que notre système galactique, la nébuleuse d’Andromède et d’autres nébuleuses proches pourraient constituer un nuage similaire.
Les profondeurs les plus reculées de l’espace. Hubble estime que la plus lointaine des 2 000 000 nébuleuses révélées par le télescope de 100 pouces doit se trouver à environ 140 millions d’années-lumière de nous. C’est la plus grande distance que l’œil humain ait jamais observée dans l’espace. Les 220 000 années-lumière qui formaient le diamètre du système galactique semblaient d’abord incroyablement grandes, mais nous parlons maintenant de distances environ 600 fois plus grandes. Pendant presque un cinquantième de son long voyage, la lumière qui nous permet de voir cette nébuleuse visible, la plus lointaine, s’est dirigée vers une Terre inhabitée. Juste au moment où elle allait arriver, l’homme est apparu sur Terre et a construit des télescopes pour la capter. C’est du moins ce qu’il paraît à l’échelle astronomique. Pourtant, même cette dernière 500e partie du voyage couvre la vie de 10 000 générations d’hommes, à travers lesquelles, ainsi que sur une période de temps 500 fois plus grande, la lumière a continué à voyager régulièrement à 186 000 miles par seconde.
Il y a tellement de nébuleuses faibles à la limite de vision du télescope de 100 pouces qu’il semble certain qu’un télescope encore plus grand en révélerait bien plus. Le télescope de 200 pouces, dont on espère la construction prochaine, doté d’une ouverture deux fois supérieure à celle du télescope actuel de 100 pouces, devrait sonder deux fois plus loin dans l’espace et pourrait donc révéler environ huit fois plus de nébuleuses, soit 16 millions.
[ p. 74 ]
¶ La structure de l’univers
Jusqu’à présent, chaque augmentation de la puissance télescopique nous a propulsés toujours plus profondément dans l’espace, et l’espace semble s’étendre à un rythme toujours plus soutenu. On peut se demander si cette expansion est vouée à l’infini : existe-t-il des limites à l’étendue de l’espace ?
Il y a une génération à peine, je pense que la plupart des scientifiques auraient répondu à cette dernière question par la négative. Ils auraient soutenu que l’espace ne pouvait être limité que par la présence de quelque chose qui n’en était pas. Nous, ou plutôt notre imagination, ne pourrions être empêchés de voyager éternellement dans l’espace qu’en nous heurtant à un mur de quelque chose de différent de l’espace. Et, aussi difficile soit-il d’imaginer l’espace s’étendant à l’infini, il est encore plus difficile d’imaginer une barrière de quelque chose de différent de l’espace qui empêcherait notre imagination de s’étendre plus loin.
L’argument est fallacieux. Par exemple, la surface terrestre est limitée, mais rien ne nous empêche de voyager aussi loin que nous le souhaitons. Un voyageur qui ne comprendrait pas la sphère terrestre s’attendrait naturellement à ce que des voyages de plus en plus longs depuis chez lui lui ouvrent sans cesse de nouvelles contrées à explorer. Or, comme nous le savons, il serait nécessairement réduit, avec le temps, à répéter ses propres traces. Du fait de sa courbure, la surface terrestre, bien qu’illimitée, est d’étendue finie.
¶ La théorie de la relativité
Par sa théorie de la relativité, Einstein prétend avoir établi que l’espace, bien qu’il soit illimité, est lui aussi d’étendue finie. Le volume total de l’espace dans l’univers est de quantité finie, tout comme la surface de la Terre, et pour la même raison : tous deux se replient sur eux-mêmes et se ferment. L’analogie n’est valable et utile que si l’on prend soin de comparer l’espace tout entier à la surface de la Terre, et non à son volume. Le volume de la Terre est également de quantité finie, mais pour des raisons tout à fait différentes. Une taupe qui creuserait la Terre en ligne droite, sans cesse, finirait par atteindre quelque chose qui n’est pas la Terre ; elle émergerait à l’air libre ; mais nous pouvons parcourir la surface de la Terre sans jamais rien rencontrer qui ne soit la surface de la Terre. Les propriétés de l’espace sont celles de la surface, et non du volume, de la Terre.
Du fait de la courbure de l’espace, un projectile ou un rayon lumineux peut voyager indéfiniment sans sortir de l’espace pour atteindre quelque chose qui n’est pas l’espace, et pourtant il ne peut continuer indéfiniment sans répéter ses propres traces. C’est pourquoi il est probable que la lumière puisse parcourir tout l’espace et revenir à son point de départ. Ainsi, si nous pointions un télescope suffisamment puissant dans la bonne direction dans le ciel de minuit, nous verrions le Soleil et ses voisins spatiaux grâce à la lumière ayant fait le tour de l’univers. Nous ne les verrions pas tels qu’ils sont aujourd’hui, mais tels qu’ils étaient il y a des millions d’années. La lumière qui avait quitté le Soleil il y a si longtemps aurait parcouru presque tout l’espace, puis, juste au moment où elle s’apprêtait à boucler la boucle, elle serait capturée par notre télescope au lieu d’entamer son second voyage spatial.
Cette courbure de l’espace a d’autres fonctions que celle qu’elle remplit à grande échelle, à savoir limiter le volume total de l’espace. Avant l’époque d’Einstein, les courbures des trajectoires des planètes, des balles de cricket et des projectiles en général étaient toutes attribuées à l’attraction d’une « force » gravitationnelle. La théorie de la relativité rejette cette prétendue force comme une pure illusion et attribue les trajectoires courbes des projectiles de toutes sortes à leurs efforts pour maintenir une trajectoire rectiligne dans un espace courbe. Cet espace courbe n’est pas, il est vrai, l’espace ordinaire de l’astronome. C’est un espace purement mathématique et probablement entièrement fictif, dans lequel l’espace et le temps des astronomes sont inextricablement liés et entrent en partenaires égaux. Pour être absolument exact, il y a quatre partenaires égaux. Les trois premières sont les trois dimensions de l’espace ordinaire : largeur, largeur et hauteur, ou, si l’on préfère, nord-sud, est-ouest et haut-bas. La quatrième est le temps ordinaire mesuré d’une manière appropriée à la façon dont nous avons mesuré notre espace (une année de temps correspondant à une année-lumière d’espace, etc.), puis multiplié par la racine carrée de — 1. Cette dernière multiplication par la racine carrée de — 1 est bien sûr le point remarquable de toute l’affaire. Car la racine carrée de — 1 n’a pas d’existence réelle ; c’est ce que le mathématicien décrit comme un nombre « imaginaire ». Aucun nombre réel ne peut être multiplié par lui-même et donner — 1 comme produit. Pourtant, ce n’est que lorsque le temps est mesuré en termes d’une unité imaginaire de années qu’il existe une véritable association égale entre l’espace et le temps. Cela montre que cette association égale est purement formelle ; ce n’est qu’une fiction commode du mathématicien. En effet, si cela avait été quelque chose de plus, notre conviction intuitive que le temps est quelque chose d’essentiellement différent de l’espace n’aurait pu avoir aucun fondement dans l’expérience et aurait donc disparu avant maintenant.
[ p. 77 ]
Ces complications liées au temps ne doivent pas nous préoccuper ici ; le point essentiel est que la théorie de la relativité d’Einstein enseigne que l’espace finit par se replier sur lui-même comme la surface de la Terre, de sorte que la quantité totale d’espace est finie.
La cosmologie d’Einstein. Selon la théorie originelle d’Einstein, les dimensions de l’espace sont déterminées par la quantité de matière qu’il contient. Plus il y a de matière, plus l’espace doit être petit, et inversement ; l’espace ne pourrait être d’étendue littéralement infinie que s’il ne contenait aucune matière. Le problème de la détermination de l’étendue de l’espace se réduit donc à celui de la quantité de matière qu’il contient. Nous n’avons aucun moyen d’estimer la quantité de matière présente en dehors des régions de l’espace accessibles à nos télescopes, mais à l’intérieur de ces régions, la matière semble être répartie assez uniformément sous forme de nébuleuses extragalactiques.
D’après les poids connus de ces particules, Hubble estime que la densité moyenne de la matière dans l’espace doit être d’environ 1,5 x 10-31 fois celle de l’eau. En supposant que la matière soit distribuée avec cette densité dans tout l’espace, y compris dans les zones que nos télescopes n’ont pas encore pénétrées, nous pouvons calculer avec une certitude absolue que le rayon de l’espace est de 84 000 millions d’années-lumière, soit 600 fois la distance de la nébuleuse visible la plus lointaine. Le tour de l’espace prendrait 500 000 millions d’années-lumière, et si jamais nos télescopes nous montrent le système solaire vu de derrière, nous le verrons tel qu’il était il y a 500 000 millions d’années.
Ainsi, selon la théorie originale d’Einstein, même les 140 millions d’années-lumière que nous pouvons parcourir avec nos télescopes ne représentent qu’une petite fraction de l’espace total – quelque chose comme une partie sur mille [ p. 78 ] million. Il reste encore beaucoup d’espace à explorer. Ce n’est peut-être pas surprenant. L’humanité, qui n’a possédé de télescopes que pendant 300 ans sur les 300 000 de sa résidence sur Terre, pouvait difficilement espérer découvrir la totalité de l’espace en si peu de temps. Nos astronomes explorateurs se déplacent d’île en île dans le petit archipel qui entoure leur foyer spatial, mais ils sont encore loin d’avoir fait le tour du monde. Et, tout comme les premiers géographes ont essayé d’estimer la taille de la Terre, bien avant de penser à la contourner, à partir de la courbure d’une petite partie de sa surface, les astronomes essaient maintenant de former des estimations, bien que nécessairement vagues, de la taille de l’univers entier à partir de la courbure de cette partie de celui-ci qu’ils connaissent déjà.
La théorie de la relativité générale a depuis longtemps dépassé le stade de la spéculation intéressante. Non seulement elle rend compte des phénomènes de mouvement planétaire devant lesquels la loi de la gravitation de Newton échouait, mais elle a également prédit d’autres phénomènes – les déplacements apparents des étoiles proches du Soleil lors d’une éclipse, résultant de la courbure de la lumière qui les observe lorsqu’elle traverse le champ gravitationnel solaire, et un certain déplacement des spectres stellaires vers le rouge – qui étaient totalement insoupçonnés lors des premières prédictions, mais qui ont été pleinement confirmés par l’observation. De fait, cette théorie est désormais considérée comme l’un des outils de travail courants de l’astronomie. Il a été utilisé pour mesurer le diamètre de la petite étoile faible Sirius B, la compagne de Sirius (p. 262), ainsi que pour discuter de la nature des étoiles au centre des « nébuleuses planétaires » (p. 323).
[ p. 79 ]
Néanmoins, la théorie de la relativité générale ne mène pas à la cosmologie d’Einstein de manière unique. Il est parfaitement possible que la première soit vraie et la seconde fausse. La théorie de la relativité générale fixe avec certitude les attributs de chaque petite fraction de l’univers, mais laisse ouvertes plusieurs voies alternatives permettant de les assembler pour former un tout. La vision particulière d’Einstein du cosmos ne peut donc prétendre au prestige qui s’attache à la théorie de la relativité générale dans son ensemble. De fait, pendant quelques années, elle tomba quelque peu en désuétude, et sembla devoir être supplantée par une cosmologie alternative, proposée et développée en détail par de Sitter de Leyde en 1917.
La cosmologie de De Sitter. Essayons d’abord de comprendre les différences essentielles entre ces deux cosmologies.
La cosmologie d’Einstein suppose que la taille du cosmos est déterminée par la quantité de matière qu’il contient. S’il fut décidé, lors de la création, de créer un univers contenant une certaine quantité de matière soumise à certaines lois naturelles, alors l’espace dut s’ajuster immédiatement à la taille appropriée pour contenir précisément cette quantité de matière, et pas plus. Ou, si la taille de l’univers et les lois naturelles étaient décidées, la création d’une quantité définie de matière devint une nécessité inévitable. L’univers de De Sitter est moins simple, ou, si l’on préfère le dire, laissait plus de liberté de choix dans sa création. Une fois les lois de la nature fixées, il était encore possible de créer un univers de n’importe quelle taille et d’y introduire n’importe quelle quantité de matière, dans certaines limites. D’un point de vue strictement scientifique, l’univers d’Einstein présente un élément d’arbitraire de moins que celui de De Sitter [ p. 80 ] univers, et dans cette mesure, il a l’avantage de la simplicité.
D’un autre côté, cette simplicité a un prix. La pierre angulaire de toute la théorie de la relativité est l’égalité de partenariat entre l’espace et le temps, au sens déjà expliqué. La cosmologie d’Einstein ne gagne sa simplicité qu’au prix de supposer que cette égalité de partenariat disparaît lorsque l’on considère le cosmos dans son ensemble. Elle suppose que l’espace et le temps ne sont indiscernables (au sens purement formel déjà indiqué) que pour un être dont l’expérience se limite à une petite fraction de l’univers ; ils deviennent totalement distincts pour un être qui peut parcourir l’ensemble de l’espace et du temps. On ne voit pas très bien quel poids accorder à cette objection, si objection il y a. L’espace et le temps réels sont indéniablement distincts. Même si nous nions la réalité de l’un et de l’autre, ils demeurent néanmoins distinguables en tant que modes de perception. Quel reproche peut-on alors faire à une cosmologie d’admettre qu’en dernier ressort, lorsque l’univers est envisagé à grande échelle, l’espace et le temps se résolvent en types d’entités distincts ? D’une certaine manière, nous le savions déjà, avant même de commencer à contempler l’univers à grande échelle.
Quelle que soit la réponse à cette dernière question, la cosmologie de de Sitter évite tout reproche en maintenant l’égalité de l’espace et du temps, non seulement dans les fractions individuelles du cosmos, mais dans tout le cosmos. Il est bien entendu que nous parlons toujours d’égalité au sens purement formel déjà expliqué, une année-lumière entrant dans la cosmologie au même titre que la racine carrée de — 1 an. Même la cosmologie de de Sitter ne prétend pas qu’une année-lumière (9,46 millions de millions de kilomètres) soit la même chose que douze mois.
Bien que la théorie principale de la relativité d’Einstein ait été amplement confirmée par l’observation, sa partie cosmologique n’a pas prédit de caractéristiques particulières, comme le permettrait un test d’observation directe. La cosmologie de De Sitter, en revanche, prédisait que les spectres de tous les objets lointains devaient présenter un déplacement vers le rouge, d’une ampleur dépendant de la distance de l’objet. L’association égale de l’espace et du temps fait que les vibrations des ondes lumineuses émises par une source donnée sont plus lentes dans les parties éloignées que dans les parties proches de l’univers ; le cours du temps s’écoule plus rapidement là où nous nous trouvons que partout ailleurs. Cela semble paradoxal à première vue, mais l’examen montre que ce n’est pas le cas ; De Sitter ne nous demande pas de revenir à un univers géocentrique, car il montre que l’habitant d’une étoile lointaine constaterait également que les atomes terrestres ont un temps plus lent que le sien. Le paradoxe est complètement résolu par le concept de relativité de toutes les mesures de l’espace et du temps.
Ce déplacement vers le rouge, dû à la simple distance, est propre à la cosmologie de Sitter. Il s’ajoute au déplacement que, comme toutes les cosmologies le reconnaissent, le spectre d’un corps en mouvement doit présenter comme résultat de son mouvement, ce dernier n’étant vers le rouge que si le corps s’éloigne de la Terre (p. 51). Dans la cosmologie de Sitter, les deux déplacements ne sont pas entièrement indépendants, car une caractéristique essentielle de cette cosmologie est que les corps proches tendent à s’éloigner les uns des autres. De même que des brins de paille jetés ensemble dans un ruisseau ont tendance à se séparer lorsqu’ils descendent le courant, de même les objets de l’univers de Sitter s’éloignent les uns des autres lorsqu’ils descendent le cours du temps.
Ainsi, selon la théorie de de Sitter, un déplacement des raies spectrales vers le rouge ne peut être interprété comme une preuve de mouvement ou de distance ; c’est un mélange des deux. Cela ne signifie pas que nous ayons eu entièrement tort de déduire les vitesses des étoiles du système galactique à partir des déplacements observés de leurs raies spectrales. Aucun déplacement appréciable n’est produit par la distance seule, à moins que cette distance ne représente une fraction appréciable du rayon de l’univers. Des déplacements systématiques vers le rouge sont, il est vrai, observés dans les spectres des étoiles les plus lointaines, mais ils sont de très faible ampleur. Ce n’est qu’en observant les nébuleuses extragalactiques lointaines que nous pouvons espérer observer cet effet avec une intensité appréciable.
Le déplacement uniforme des spectres des nébuleuses lointaines vers le rouge est depuis longtemps l’une des principales énigmes de l’astronomie. Les déplacements observés ne sont pas négligeables. Interprétés comme des vitesses, nombre d’entre eux représenteraient des vitesses supérieures à 1 600 kilomètres par seconde. Humason a découvert que deux nébuleuses peu lumineuses, NGC 4860 et 4853, présentent des vitesses de récession apparentes respectives de 7 900 et 7 400 kilomètres par seconde. Elles font toutes deux partie d’un nuage de nébuleuses dans la Chevelure de Bérénice (p. 72), probablement à une distance d’environ 50 millions d’années-lumière. Plus récemment, le spectre d’une autre nébuleuse très faible de la Grande Ourse a montré un mouvement de récession apparent à une vitesse de 11 600 kilomètres par seconde. Si la théorie de de Sitter est rejetée, presque toutes les nébuleuses extragalactiques doivent s’éloigner de nous à des vitesses effroyables, presque inimaginables. Et plus elles s’éloignent [ p. 83 ], plus leur distance augmente rapidement. Pourtant, on peut difficilement rétablir la simplicité en adoptant la théorie de de Sitter et en considérant toute cette apparente ruée de nébuleuses comme une illusion, puisque cette théorie implique que les nébuleuses pourraient bien, en réalité, s’éloigner de nous, la diffusion étant une propriété inhérente aux objets d’un univers de de Sitter.
Le fait que les spectres des nébuleuses les plus lointaines présentent ces grands déplacements fournit une certaine présomption en faveur de la véracité de la cosmologie de Sitter ; cela les explique au moins deux fois, alors qu’aucune autre cosmologie ne les explique du tout. Si nous acceptons provisoirement cette cosmologie, alors chaque décalage spectral observé doit être considéré comme la somme de deux parties, l’une résultant normalement d’un recul de la nébuleuse, et l’autre résultant simplement de son éloignement.
Une étude préliminaire du Dr Hubble a montré que, globalement, les déplacements spectraux sont plus importants pour les nébuleuses les plus éloignées, et que leurs valeurs sont approximativement proportionnelles à leur distance par rapport à nous. Si nous interprétons l’ensemble des déplacements observés uniquement comme une preuve de récession, nous pouvons calculer que le rayon de l’univers est d’environ 2 milliards d’années-lumière, soit environ quatorze fois la distance de la nébuleuse visible la plus éloignée. Avec un rayon de l’univers aussi grand, le déplacement supplémentaire résultant de la simple distance des nébuleuses, même éloignées, est négligeable, de sorte que notre hypothèse selon laquelle les déplacements résultent presque entièrement des vitesses de récession est confirmée a posteriori. Si les déplacements observés des spectres nébuleux avaient été strictement proportionnels à leur distance par rapport à nous, nous aurions obtenu une explication cohérente des faits observés par [ p. 84 ] en supposant que nous vivions dans un univers de Sitter ayant un rayon d’environ 2000 millions d’années-lumière.
L’Univers en expansion. On pensait autrefois que les cosmologies d’Einstein et de Sitter étaient antagonistes, car aucun univers ne pouvait être à la fois un univers d’Einstein et un univers de Sitter. Une étude récente menée par un mathématicien belge, l’abbé G. Lemaitre, a apporté une autre perspective au problème. En bref, Lemaitre a démontré qu’aucun univers ne pouvait rester en permanence dans l’état considéré par Einstein. Un univers dans cet état est une structure instable ; dès sa naissance, il commencerait à s’étendre et ne cesserait de s’étendre que lorsqu’il deviendrait un univers de Sitter. Même après cela, l’expansion se poursuivrait, mais elle se fondrait alors dans l’expansion normale de l’univers de Sitter, telle que nous l’avons déjà envisagée.
À la lumière de ces résultats, la question n’est pas de savoir si notre univers est un univers d’Einstein ou un univers de Sitter, mais plutôt de savoir jusqu’où il a parcouru le chemin qui commence par un univers d’Einstein et se termine par un univers de Sitter. Quelle que soit la réponse, nous sommes amenés à supposer qu’au début des temps, les nébuleuses étaient beaucoup plus proches les unes des autres qu’elles ne le sont aujourd’hui, que depuis lors, elles ont obéi à leur tendance inhérente à se disperser, ou plutôt à la tendance du cours du temps à les disperser, et qu’elles s’éloignent maintenant de nous, et les unes des autres, à des vitesses proportionnelles à leurs distances. Ceci est conforme à la conclusion de Hubble, selon laquelle les vitesses apparentes de récession des nébuleuses sont approximativement proportionnelles à leurs distances. À partir des données de Hubble, Eddington a calculé que [ p. 85 ] L’univers originel d’Einstein devait avoir un rayon d’environ 1 200 millions d’années-lumière. Si les vitesses apparentes de récession des nébuleuses s’étaient avérées strictement proportionnelles à leurs distances, nous aurions pu tout expliquer en supposant que nous vivions dans un univers en expansion, qui avait commencé comme un univers d’Einstein de 1 200 millions d’années-lumière de rayon, s’était maintenant étendu à un rayon de l’ordre de 2 000 millions d’années-lumière et était destiné à poursuivre son expansion pour l’éternité.
Ceci donne une image simple et plutôt fascinante de l’univers, mais de nombreuses raisons s’opposent à sa véracité. Tout d’abord, si l’on interprète les déplacements spectraux comme la seule preuve de la vitesse, les vitesses des nébuleuses sont probablement très loin d’être (comme le suggère l’image précédente) exactement proportionnelles à leur distance. Un groupe de trois nébuleuses, toutes supposées se trouver à la même distance d’environ 50 millions d’années-lumière, présentent une différence de vitesse de près de 3 200 kilomètres par seconde, qui est en moyenne d’environ 8 000 kilomètres par seconde. Oort a constaté une tendance générale à ce que les vitesses des nébuleuses très éloignées ne soient pas strictement proportionnelles à leur distance. Entre 20 et 40 millions d’années-lumière, les divergences apparentes sont en moyenne de 1 200 kilomètres par seconde, mais on ne sait pas clairement dans quelle mesure elles résultent simplement d’estimations inexactes des distances de ces nébuleuses lointaines.
En second lieu, si les décalages spectraux observés représentent une simple diffusion, nous pouvons calculer le temps écoulé depuis le début de cette diffusion ; il s’avère qu’il s’élève à plusieurs milliards d’années. Aussi énorme que soit cette durée, elle ne semble pas suffisante. Nous verrons plus loin (Chapitre III) comment le temps laisse sa marque, ses rides et ses cheveux gris, sur les étoiles, de sorte que nous pouvons deviner assez bien leur âge, et les preuves [ p. 86 ] sont toutes en faveur d’une vie stellaire, non pas de milliards, mais de millions de millions d’années. Si les nébuleuses doivent leurs mouvements actuels à une simple diffusion, alors les étoiles doivent avoir vécu la plus grande partie de leur vie avant le début de cette diffusion. Une telle hypothèse semble trop artificielle pour être acceptée, du moins tant qu’une alternative est ouverte.
Bien sûr, nous devons admettre franchement que nos estimations de l’âge des étoiles pourraient nécessiter une révision. En effet, elles ont été calculées en supposant qu’aucune diffusion notable du type requis par la cosmologie de Sitter ne s’est jamais produite. Si non seulement les nébuleuses, mais aussi les étoiles composant le système galactique, étaient regroupées au début des temps, nos estimations de la durée de vie des étoiles devraient être considérablement raccourcies, et il est concevable, bien que très improbable à mon avis, qu’elles puissent être réduites à des longueurs du type de celles que nous venons d’examiner ; elles ne pourraient certainement pas l’être si l’univers originel avait un rayon proche de l’estimation d’Eddington, soit 1 200 millions d’années-lumière.
Néanmoins, les cosmologies de de Sitter et de Lemaitre exigent sans aucun doute que l’univers actuel soit en expansion, que les nébuleuses s’éloignent les unes des autres et de nous, et que leurs spectres présentent, par conséquent, des déplacements vers le rouge. Mais rien ne nous oblige à identifier ces déplacements avec ceux effectivement observés. De nombreuses causes, autres que les mouvements de récession, sont susceptibles de rougir les raies spectrales, et ce n’est qu’après avoir déduit tout le rougissement dû à ces diverses autres causes que nous pourrons affirmer que le résidu représente un véritable mouvement de récession.
Tout récemment, le Dr Zwicky de Pasadena a suggéré [ p. 87 ] que la matière gravitationnelle diffusée dans l’espace pourrait rougir toute la lumière qui le traverse. Il justifie sa suggestion par des arguments dynamiques, calcule l’ampleur du décalage spectral prévisible dans la lumière nous parvenant des nébuleuses et constate qu’il expliquerait la quasi-totalité du décalage observé. Il est possible que la majeure partie du rougissement observé de la lumière nébulaire soit due à cette cause ou à une cause similaire, seule une petite fraction représentant de véritables mouvements de récession. Si tel est le cas, nous pouvons prolonger indéfiniment l’âge de l’univers et sommes libres d’attribuer aux étoiles les âges très élevés que les données de l’astronomie générale semblent exiger. Nous aborderons ce sujet en détail au chapitre 1.
Dans la version originale de cette cosmologie de de Sitter, la lumière mettrait un temps infini pour faire le tour de l’univers, ce qui empêcherait tout objet d’être vu par la lumière ayant parcouru le long chemin. Ceci résulte du fait que de Sitter n’a considéré que le cas idéal d’un univers entièrement vide de toute matière. Avec même un peu de matière dans l’univers, la trajectoire d’un rayon lumineux se courberait probablement sur elle-même et reviendrait à son point de départ après un temps fini. Il a été sérieusement suggéré que deux nébuleuses faibles (h 3433 et M 83) pourraient en fait être nos deux plus proches voisines dans le ciel, M 33 et M 31, vues du long chemin de l’espace. Si tel est le cas, nous voyons les faces avant de deux objets lorsque nous regardons M 33 et M 31, et les faces arrière des deux mêmes objets lorsque nous pointons nos télescopes dans des directions exactement opposées et regardons h 3433 et M 83. Il ne s’agit sans doute que d’une conjecture, et peut-être plutôt folle, mais de nombreuses autres conjectures surprenantes ont été faites en astronomie, et se sont avérées vraies par la suite.
[ p. 88 ] Toutes ces discussions sur la structure de l’espace sont bien sûr hautement spéculatives, mais elles s’accordent à suggérer la conclusion générale que, si nous ne pouvons pas encore voir l’espace dans son intégralité, nous pouvons au moins en examiner une fraction appréciable. Nos astronomes-explorateurs n’ont peut-être pas encore fait le tour du monde, mais ils découvrent peut-être l’Amérique, et nous pouvons bien imaginer que même la prochaine génération aura achevé le tour du monde et pensera à un espace fini mais illimité de la même manière, et avec la même facilité, que nous pensons à la surface finie mais illimitée de la Terre.
¶ Un modèle de l’univers
Nous avons déjà eu du mal à visualiser les 4¼ années-lumière qui constituent la distance à l’étoile la plus proche. Il serait donc judicieux de ne même pas tenter de visualiser cette dernière distance de plusieurs milliards d’années-lumière, soit la circonférence supposée de l’univers. Pourtant, nous pouvons essayer de visualiser toutes ces distances dans des proportions appropriées les unes par rapport aux autres à l’aide d’un modèle à l’échelle. Nous pouvons éviter d’essayer d’imaginer des distances inimaginables en gardant une échelle très petite.
La Terre, voyageant 1 200 fois plus vite qu’un train express, parcourt chaque année 960 millions de kilomètres autour du Soleil. Représentons ce trajet par une tête d’épingle de 3,8 mm de diamètre. Ceci fixe l’échelle de notre modèle ; le Soleil s’est réduit à un minuscule grain de poussière de 1,34 mm de diamètre, tandis que la Terre est un grain encore plus minuscule, trop petit pour être vu, même avec le plus puissant des microscopes. À cette échelle, l’étoile la plus proche dans le ciel, [ p. 89 ] Proxima du Centaure, doit être placée à environ 200 mètres, et pour contenir ne serait-ce que la centaine d’étoiles les plus proches de notre Soleil dans l’espace, le modèle doit mesurer 1,6 km de haut, 1,6 km de long et 1,6 km de large.
Poursuivons la construction du modèle. On peut considérer les étoiles indistinctement comme des grains de poussière, car leurs tailles varient à peu près autant que celles des grains de poussière. Au voisinage du Soleil, il faut placer les grains de poussière à des distances moyennes d’environ 400 mètres. Dans d’autres régions de l’espace, ils sont généralement encore plus éloignés, car, en raison de la présence de l’« amas local », le voisinage immédiat du Soleil se trouve être une zone du ciel plutôt encombrée. Nous continuons à construire le modèle sur des centaines de kilomètres dans toutes les directions, puis, si nous construisons dans une direction éloignée du plan galactique, les grains de poussière commencent à s’éclaircir ; nous approchons des confins de la galaxie. Dans le plan galactique lui-même, nous construisons sur environ 11 000 kilomètres avant d’atteindre l’amas globulaire le plus éloigné, et nous sommes toujours à l’intérieur du système galactique. Avec le long voyage annuel de notre Terre autour du Soleil comme une tête d’épingle, le système galactique tout entier a environ la taille du continent américain. Il serait peut-être judicieux de faire une pause et d’essayer de visualiser les tailles relatives d’une tête d’épingle et du continent américain, avant de poursuivre la construction de notre modèle mental.
Une fois le système galactique terminé, nous devons parcourir environ 48 000 kilomètres avant de commencer à construire la partie suivante de notre modèle, du moins si nous le maintenons à l’échelle. À cette distance, nous plaçons la famille d’étoiles suivante, une famille probablement beaucoup plus petite et plus compacte que notre propre famille galactique, mais comparable en taille et en nombre. Nous continuons donc à construire notre modèle – une famille de milliers [ p. 90 ] de millions d’étoiles tous les 48 000 kilomètres environ – jusqu’à atteindre deux millions de familles de ce type. Le modèle s’étend maintenant sur environ quatre millions de kilomètres dans toutes les directions. Cela représente l’étendue maximale que nous pouvons observer dans l’espace avec un télescope ; nous pouvons imaginer la progression du modèle, bien que nous ignorions comment ni où ; tout ce que nous savons, c’est que la partie construite jusqu’ici ne représente qu’une fraction de l’univers.
Chaque système galactique, univers insulaire ou nébuleuse extragalactique contient des milliards d’étoiles, ou de la matière gazeuse destinée à former des milliards d’étoiles. Nous connaissons deux millions de systèmes de ce type. Il y a donc des milliards de millions d’étoiles dans le champ de vision du télescope de 2,54 m, et ce nombre doit être multiplié pour prendre en compte les parties de l’univers encore inexplorées. Un calcul modéré montre que le nombre total d’étoiles dans l’univers doit être comparable au nombre total de grains de poussière à Londres. Imaginez le Soleil comme un peu moins qu’un grain de poussière dans une vaste ville, la Terre comme moins d’un millionième de ce grain de poussière, et nous obtenons peut-être l’image la plus saisissante possible de la relation entre notre foyer spatial et le reste de l’univers.
Une autre procédure aurait consisté à construire notre maquette en prenant tous les grains de poussière de Londres et en les répartissant aux distances adéquates pour représenter les différentes étoiles de l’espace. La distance moyenne réelle entre les grains de poussière à Londres est d’une fraction de pouce ; pour que notre maquette soit à l’échelle correcte, cette distance doit être augmentée à environ un quart de mile, même lorsque nous construisons la partie représentant l’espace encombré autour du Soleil. Si nous construisons notre maquette de cette manière, nous obtenons [ p. 91 ] une image saisissante du vide spatial. La gare de Waterloo est vidée de tout, sauf de six grains de poussière, et elle est encore bien plus encombrée de poussière que l’espace ne l’est d’étoiles. Cela est vrai même pour la région relativement encombrée du système galactique ; cela ne tient pas compte des immenses étendues vides entre un système stellaire et le suivant. En moyenne sur l’ensemble du modèle, la distance moyenne entre un grain de poussière et son plus proche voisin s’élève à environ 130 kilomètres. L’univers est principalement constitué non pas d’étoiles, mais de vide désolé – d’immenses étendues désertiques où la présence d’une étoile est un événement rare et exceptionnel.
Imaginons-nous dans l’espace, quelque part près du Soleil, et observons les étoiles défiler à une vitesse environ mille fois supérieure à celle d’un train express. Si l’espace était réellement peuplé d’étoiles, notre position serait aussi peu enviable que si nous nous asseyions au milieu de Regent Street à regarder passer la circulation ; notre vie, bien que palpitante, serait brève. Pourtant, comme le montrent des calculs précis, le trafic stellaire est si faible qu’il nous faudrait attendre environ un million de millions de millions d’années avant qu’une étoile ne nous percute. En d’autres termes, le calcul montre qu’une étoile peut s’attendre à se déplacer pendant environ un million de millions de millions d’années avant d’entrer en collision avec une seconde étoile. Les étoiles se déplacent à l’aveuglette dans l’espace, et les acteurs de ce jeu de colin-maillard stellaire sont si rares que la probabilité de rencontrer une autre étoile est presque négligeable. Nous verrons plus loin que ce concept est d’une importance capitale pour notre interprétation de l’univers.
¶ Notes de bas de page
[^2] : Soit C le centre de la Terre et bCD le diamètre passant par b. Alors BA2 = Bb x BD, où Bb = 16 pieds, et BD, qui est 16 pieds de plus que le diamètre de la Terre = 41 900 000 pieds. De là, nous calculons facilement que BA = 25 880 pieds. Ce calcul néglige bien sûr la hauteur de la colline AA’ par rapport au diamètre de la Terre.
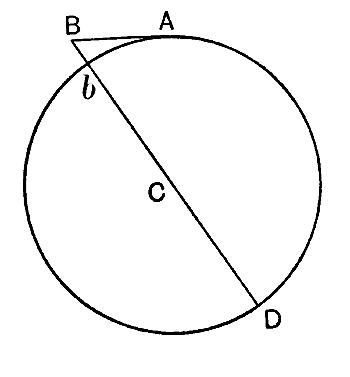
[^4] : La notation 6 x 1021 représente le nombre formé par un 6 suivi de 21 zéros, cette notation abrégée étant essentielle, par souci de concision, pour discuter des nombres astronomiques. Un million vaut 106, un million de millions vaut 1012, et ainsi de suite.
Une notation similaire est nécessaire pour exprimer de très petits nombres. L’expression 10-21 s’écrit pour et ainsi de suite. Ainsi, 6 x 10-6 correspond à 6/1 000 000, soit 0,000006.
Car la luminosité apparente d’un objet diminue comme l’inverse du carré de sa distance, et le carré de 80 000 est approximativement égal à 6 000 millions. ↩︎
Ici, comme tout au long du livre, nous utilisons la tonne française ou métrique d’un million de grammes ou 2204,5 livres. La tonne anglaise de 2240 livres est égale à 10160 tonnes françaises. ↩︎
La définition la plus simple d’une ellipse est qu’elle est la courbe tracée par un point mobile P qui se déplace de telle manière que la somme de ses distances PS, PT à partir de deux points fixes S, T reste toujours la même. En pratique, nous pouvons facilement dessiner une ellipse en glissant une ficelle sans fin SPTS autour de deux punaises S, T plantées dans une planche à dessin. Tendez la ficelle avec un crayon en P, et en laissant le crayon se déplacer, en gardant la ficelle toujours tendue, nous dessinerons une ellipse. Si les punaises S, T de la planche à dessin sont placées près l’une de l’autre, la courbe décrite par le crayon P est presque circulaire. Le rapport de la distance ST à la longueur du reste de la ficelle SP + PT est appelé « excentricité » de l’ellipse ; il est nécessairement inférieur à l’unité, car deux côtés d’un triangle sont ensemble plus grands que le troisième côté.
Dans le cas limite où l’excentricité est nulle, l’ellipse devient un cercle. Si l’excentricité est proche de l’unité, l’ellipse est très allongée. Toutes les formes d’ellipses sont obtenues en faisant varier l’excentricité de 0 à 1, et elles représentent toutes les formes d’orbite qu’un petit corps peut décrire autour d’une masse gravitationnelle lourde. Les points S et T sont appelés les foyers de l’ellipse, et le grand corps attractif occupe toujours l’un ou l’autre des deux foyers de l’ellipse. ↩︎Ce qu’il observe en réalité est la « projection » de l’orbite sur le ciel, mais c’est un théorème bien connu de la géométrie que la projection d’une ellipse est toujours une ellipse. ↩︎
Par exemple, les Céphéides dont la lumière fluctue sur une période de 40 heures ont une luminosité approximativement 250 fois supérieure à celle du Soleil, et sont donc de 8 x 1029 bougies-puissance ; une période de dix jours indique une luminosité 1600 fois supérieure à celle du Soleil, soit une bougie-puissance de 5,17 x 1030, et ainsi de suite. Si une étoile dans un objet astronomique lointain est observée fluctuant sur une période de dix jours, et que la qualité de ses fluctuations montre qu’il s’agit d’une variable Céphéide, nous savons que sa bougie-puissance réelle doit être de 5,17 x 1030. Sa luminosité apparente est observée comme étant celle d’une étoile de, disons, magnitude 16, ce qui, dépouillé de toute technicité, signifie que nous recevons autant de lumière d’elle que d’une seule bougie à une distance de 570 miles. La différence entre une bougie et 5,17 x 1030 bougies correspond donc à la différence entre 570 miles et la distance de l’objet en question, d’où, puisque la lumière tombe comme l’inverse du carré de la distance, nous calculons que la distance de l’objet doit être
soit environ 220 000 années-lumière. ↩︎