Autor: Sir James Jeans, M. A., D. Sc., Sc. D., LL. D., F. R. S.
[ p. 194 ] Hemos comentado el sorprendente vacío del espacio: seis motas de polvo en la estación de Waterloo representan hasta qué punto está ocupada por estrellas en sus partes más concurridas. El comentario bien podría haber tomado otra forma. Seis motas de polvo contienen, digamos, mil millones de millones de moléculas. Nuestro modelo de espacio está vacío porque esta gran cantidad de moléculas se agregan todas en tan solo seis grumos. En el espacio real, la unidad de agregación es la estrella, y una estrella promedio contiene alrededor de 1056 moléculas, un número tan grande que es bastante inútil tratar de imaginarlo. El vacío del espacio no se origina en ninguna escasez de moléculas; tiene su origen en la circunstancia de que, aparte de las que forman las tenues nubes de gas que se extienden de estrella en estrella, las moléculas se agregan en las enormes colonias que llamamos estrellas, con unos 1056 miembros cada una. ¿Por qué las moléculas en el espacio deberían agruparse de esta manera, cuando las moléculas en las habitaciones en las que estoy escribiendo y tú leyendo no lo hacen?
Siguiendo un método científico bien probado, podemos intentar descubrir por qué se han formado estos agregados, examinando primero qué los mantiene juntos ahora que se han formado. La atmósfera terrestre se compone de unas 1041 moléculas. ¿Por qué permanecen presionados en una atmósfera en lugar de esparcirse por el espacio? La respuesta, por supuesto, la proporciona la gravitación de la tierra. Una bala disparada desde la superficie de la tierra con una velocidad de 6,93 millas [11 km/s] por segundo o más volará hacia el espacio, porque la atracción gravitatoria de la tierra es [ p. 195 ] inadecuada para retenerla cuando se mueve a una velocidad tan alta. Pero una bala disparada con una velocidad de menos de 6,93 millas [11 km/s] por segundo no sale de la tierra; su velocidad es inadecuada para librarse de la atracción de la tierra. Así, las moléculas-balas que forman la atmósfera terrestre, volando a velocidades inferiores a un tercio de milla por segundo, no tienen posibilidad alguna de escapar. La gravedad de la tierra los atrae continuamente hacia la tierra, de modo que la tierra retiene su cubierta de aire.
En intervalos raros, una molécula puede experimentar una sucesión de colisiones excepcionalmente afortunadas con otras moléculas, y así alcanzar una velocidad de más de 6,93 millas por segundo. Una molécula que llega al exterior de la atmósfera terrestre con tal velocidad abandonará la Tierra por completo y se unirá a la multitud interestelar de moléculas extraviadas. La tierra se despoja continuamente de su atmósfera de esta manera, pero el cálculo muestra que la pérdida, incluso en millones de millones de años, es bastante insignificante, de modo que podemos considerar la atmósfera terrestre como permanente.
Es lo mismo con el sol. El calor del sol ha descompuesto las moléculas de su atmósfera en sus átomos constituyentes, y estos se mueven a una velocidad promedio de unas 2 millas por segundo [3,2 km/s]. Pero una bala atómica tendría que moverse a unas 380 millas por segundo [611 km/s] para escapar por completo del sol, de modo que los átomos solares permanezcan para formar una atmósfera.
Si todas las moléculas de aire de una habitación ordinaria se reunieran en un grupo en el centro de la habitación, la bola de aire así formada ejercería, por supuesto, una atracción gravitatoria sobre sus moléculas más externas, del mismo tipo que la tierra y el sol en las moléculas de sus atmósferas. Pero, debido a que el peso de esta bola de aire es tan pequeño, la intensidad de su [ p. 196 ] tirón también sería pequeño; de hecho, sería tan débil que una velocidad de aproximadamente una yarda [0,9 m] por siglo sería suficiente para eliminar las moléculas más externas. Puesto que las moléculas de aire ordinario se mueven a unas 500 yardas por segundo [457 m/s], una bola de aire de este tipo se dispersaría inmediatamente por toda la habitación. Por otro lado, si la habitación fuera lo suficientemente grande como para contener el sol, todas sus moléculas podrían quedarse en una bola en el centro, tal como lo hacen en el sol. Las moléculas más externas necesitarían una velocidad de al menos 380 millas por segundo [611 km/s] para escapar, por lo que sus velocidades reales de 500 yardas por segundo [457 m/s] no les servirían.
Atmósferas planetarias. En general, la cuestión de escapar o no escapar depende del resultado de una batalla entre las velocidades moleculares de las moléculas más externas y la intensidad del control gravitatorio que el resto de la masa ejerce sobre ellas. El sistema solar proporciona muchos ejemplos de esto. La luna tiene sólo una sexta parte del control gravitatorio sobre las moléculas de una atmósfera que tiene la tierra, con el resultado de que cualquier atmósfera que la luna haya tenido alguna vez, ya ha escapado. Mercurio tiene dos quintas partes de la fuerza gravitatoria de la Tierra, pero debido a su proximidad al Sol, su superficie hacia el Sol está muy caliente, con la consecuencia de que su atmósfera también se ha escapado. La fuerza gravitatoria de Marte sobre sus moléculas es sólo una quinta parte de la de la Tierra, pero su superficie es más fría. Los cálculos muestran que el vapor de agua y las moléculas más pesadas deberían permanecer, mientras que las moléculas más ligeras de helio e hidrógeno deberían haber escapado. Esto probablemente representa lo que realmente sucedió. El satélite más grande de Saturno y los dos satélites más grandes de Júpiter ejercerían aproximadamente el mismo control gravitatorio que la Luna, pero como sus superficies deben ser enormemente [ p. 197 ] más frío que el de la luna, deberían poder retener atmósferas. Algunos observadores afirman haber visto indicios de atmósferas en los tres satélites. Los cuatro planetas principales ejercen una fuerza gravitatoria sobre sus moléculas más fuerte que la Tierra, y por lo tanto retienen sus atmósferas con facilidad, mientras que Venus, con aproximadamente la misma fuerza gravitatoria que la Tierra, también retiene una atmósfera.
Estas consideraciones explican ampliamente por qué las moléculas de las estrellas deben permanecer necesariamente agregadas ahora que los agregados se han formado una vez, pero la cuestión de cómo y por qué se formaron estos agregados en primera instancia es mucho más compleja. ¿Qué, por ejemplo, determinó que debería haber unas 1056 moléculas en cada estrella en lugar de 1054 o 1058?
¶ Inestabilidad gravitatoria
Es natural preguntarse si las fuerzas que ahora mantienen unidas a una estrella no pueden haber sido también responsables de su caída en primer lugar. Esto nos lleva a estudiar con cierto detalle el poder agregado de la gravitación.
Cinco años después de que Newton publicara su ley de la gravitación, Bentley, el maestro del Trinity College, le escribió, planteándole la cuestión de si la fuerza de la gravitación recién descubierta no explicaría la acumulación de materia en estrellas, y encontramos a Newton respondiendo: en carta de fecha 10 de diciembre de 1692:
Me parece que si la materia de nuestro sol y de los planetas, y toda la materia del universo, estuviera uniformemente repartida por todos los cielos, y cada partícula tuviera una gravedad innata hacia todas las demás, y todo el espacio a lo largo del cual esta materia estaba dispersa, fuera finita, la materia en el exterior de este espacio tendería por su gravedad [ p. 198 ] hacia toda la materia del interior y, en consecuencia, caería en medio de todo el espacio, y allí compondría una gran masa esférica. Pero si la materia estuviera uniformemente dispuesta en un espacio infinito, nunca podría reunirse en una sola masa; una parte se reuniría en una masa y otra en otra, de modo que formaría un número infinito de grandes masas, esparcidas a grandes distancias unas de otras por todo ese espacio infinito. Y así podrían formarse el sol y las estrellas fijas, suponiendo que la materia fuera de naturaleza lúcida.
Una investigación matemática exacta en la que me embarqué en 1901 no sólo confirma la conjetura de Newton en términos generales, sino que también proporciona un método para calcular el tamaño de los agregados que se formarían bajo la acción de la gravedad.
La formación de condensaciones. Te paras en medio de una habitación y aplaudes. En lenguaje común estás haciendo un ruido; el físico, en su capacidad profesional, diría que estás creando ondas de sonido. A medida que se acercan, tus manos expulsan las moléculas de aire intermedias. Estos salen en estampida, chocando con las moléculas de las capas exteriores de aire, que a su vez son expulsadas para chocar con capas aún más remotas; la perturbación creada originalmente por el movimiento de tus manos continúa en forma de onda. Aunque las moléculas individuales tienen una velocidad media de 500 metros por segundo, la cualidad de zig-zag de sus movimientos reduce la velocidad de la perturbación, como ya hemos visto, a unos 370 metros por segundo, la velocidad normal del sonido. A medida que la perturbación llega a cualquier punto, el número de moléculas allí se vuelve anormalmente alto, porque las moléculas en estampida se suman a la cuota normal de moléculas en ese punto. Esto por supuesto produce un exceso de presión. Es este exceso de presión que actúa sobre [ p. 199 ] mi tímpano que transmite una sensación a mi cerebro, de manera que escucho el ruido de tus palmas.
Por supuesto, este exceso de presión no puede durar mucho tiempo, de modo que el exceso de moléculas que lo produce debe disiparse rápidamente. Así es como pasa la onda. Sin embargo, hay un factor que milita en contra de su disipación. Cada molécula ejerce una atracción gravitatoria sobre todas sus vecinas, de modo que donde hay un exceso de moléculas, también hay un exceso de fuerza gravitacional. En una onda de sonido ordinaria, esto es de una cantidad absolutamente inapreciable, sin embargo, tal como es, proporciona una pequeña fuerza que retiene las moléculas y evita que se dispersen tan libremente como lo harían de otra manera. Cuando ocurre el mismo fenómeno en la escala astronómica, las fuerzas correspondientes pueden volverse de una importancia abrumadora.
Hablemos del gas en cualquier región del espacio donde el número de moléculas está por encima del promedio del espacio circundante, como una «condensación». Entonces se puede probar que, si una condensación es de suficiente extensión, el exceso de fuerza gravitacional puede ser suficiente para inhibir la dispersión por completo. En tal caso, la condensación puede crecer continuamente atrayendo moléculas desde el exterior, cuyas velocidades moleculares son entonces inadecuadas para llevarlas de nuevo.
Que esto suceda o no dependerá, por supuesto, de la velocidad del movimiento molecular en el gas, así como del tamaño de la condensación. Pero no dependerá en absoluto de la medida en que haya procedido el proceso de condensación. Al duplicar el exceso de número de moléculas en cualquier condensación, duplicamos el grado en que se ha producido la condensación. Al hacerlo, duplicamos la atracción gravitatoria que tiende a aumentar la condensación, pero también duplicamos el exceso de presión [ p. 200 ] que tiende a disiparlo; duplicamos los pesos en cada lado de la balanza, pero la balanza sigue oscilando en la misma dirección. Si una vez las condiciones son favorables para su crecimiento, una condensación sigue creciendo automáticamente hasta que no quedan más moléculas para absorber.
Cuanto mayor sea la extensión en el espacio de una condensación, las condiciones más favorables son para su crecimiento continuo. En igualdad de condiciones, una condensación de dos millones de millas de diámetro ejercerá el doble de la fuerza gravitacional de una condensación de un millón de millas de diámetro, pero el exceso de presión es el mismo en los dos casos. Así, cuanto más grande es una condensación, más probable es que siga creciendo, y al pasar en la imaginación a condensaciones cada vez más grandes, con el tiempo debemos llegar a condensaciones de tal tamaño que están obligadas a seguir creciendo. La ley de la naturaleza aquí es una de competencia sin restricciones. Nada tiene tanto éxito como el éxito, y así encontramos que las condensaciones que son grandes al principio tienen la capacidad de aumentar aún más, mientras que las que son pequeñas simplemente se disipan.
Supongamos ahora que una enorme masa de gas uniforme se extiende a través del espacio por millones de millones de millas en todas direcciones. Cualquier perturbación que destruya su uniformidad puede considerarse como la creación de condensaciones de todos los tamaños imaginables.
Esto puede no parecer obvio al principio; se puede pensar que una perturbación que sólo afectara a una pequeña área de gas sólo produciría una condensación de pequeña extensión. Tal argumento pasa por alto la forma en que la atracción gravitatoria de un cuerpo pequeño actúa en todo el universo. La luna suscita mareas en la lejana tierra, y también mareas, aunque en cantidad incomparablemente menor, en la más lejana de las estrellas. Cada vez que [ p. 201 ] el niño tira su juguete fuera de su cochecito de bebé, perturba el movimiento de cada estrella en el universo. Mientras actúe la gravitación, ninguna perturbación puede limitarse a un área inferior a la totalidad del espacio. Cuanto más violenta sea la perturbación que las crea, más intensas serán las condensaciones al principio, pero aun la más pequeña perturbación debe producir condensaciones, aunque éstas pueden ser de una intensidad extremadamente débil. Y hemos visto que el destino de una condensación no está determinado por su intensidad sino por su tamaño. Por débil que haya sido su intensidad original, las grandes condensaciones van creciendo, las pequeñas desaparecen. Con el tiempo no queda más que una colección de grandes condensaciones. El análisis matemático al que ya nos hemos referido muestra que existe un peso mínimo definido de modo que todas las condensaciones por debajo de este peso simplemente se disipan en el espacio. En una aproximación lo suficientemente buena para nuestro propósito presente, este peso mínimo es tal que si una décima parte de este peso de gas se aislara en el espacio, y todo el resto del gas fuera aniquilado, las moléculas no lograrían escapar por los pelos de su superficie[1].
Podemos decir que la masa original de gas uniformemente distribuida era «inestable» porque cualquier perturbación, [ p. 202 ] por leve que sea, hace que cambie su configuración por completo; tenía los atributos dinámicos de un palo en equilibrio sobre su punta, o de una pompa de jabón que está a punto de estallar.
Caos primigenio. Estos resultados teóricos generales ahora pueden aplicarse a cualquier masa de gas que queramos. Comencemos aplicándolos a la hipotética «materia dispuesta uniformemente en un espacio infinito» de Newton. Volvemos en la imaginación a una época en que toda la sustancia de las estrellas y nebulosas actuales se extendía uniformemente por todo el espacio; en resumen, partimos del caos primitivo del que han partido la mayoría de las teorías científicas de la cosmogonía. Hubble ha estimado que si toda la materia en esas partes del universo que conocemos se redistribuyera uniformemente por todo el espacio, el gas así formado tendría solo alrededor de 1,5 x 10-31 veces la densidad del agua. Es casi seguro que esta estimación es baja, incluso si representa las condiciones actuales, y al tratar de reconstruir el gas primitivo, debemos agregar algo para tener en cuenta las moléculas y los átomos que se han derretido en la radiación en el período intermedio. En general, quizás 10-30 no sea una densidad irrazonable para asignar a la hipotética nebulosa primigenia. Es casi inconcebiblemente bajo. En el aire ordinario, con una densidad de ocho centésimas partes de la del agua, la distancia media entre las moléculas adyacentes es de unas ocho millonésima parte de una pulgada [0,0002 mm]; en el gas primitivo que ahora estamos considerando, la distancia correspondiente es de dos o tres yardas [1,8 o 2,7 m]. El contraste vuelve a llevarnos al tema del vacío extremo del espacio.
¿Cuál es el peso mínimo de condensación que persistiría en este gas primitivo?
El cálculo muestra que si el aire ordinario fuera atenuado [ p. 203 ] en este grado extraordinario, ninguna condensación podría persistir y seguir creciendo a menos que tuviera al menos 62½ millones de veces el peso del sol; cualquier peso menor de gas ejercería una atracción gravitacional tan leve sobre sus moléculas más externas, que sus velocidades moleculares normales de 500 yardas por segundo [457 m/s] conducirían a la rápida disipación de toda la condensación.
Podemos realizar cálculos similares con referencia a otras densidades supuestas de gas y otras velocidades moleculares. La siguiente tabla muestra los pesos de las condensaciones que se formarían en masas primitivas de gas caótico con las densidades mostradas en la primera columna y las diversas velocidades moleculares mencionadas en las cabezas de las columnas restantes. En cada caso, los pesos de las condensaciones se dan en términos del peso del sol:
| Densidad en términos de agua | Vel. mol. vel. de 500 yardas por segundo [457 m/s]. | Vel. mol. de 1000 yardas por segundo [914 m/s]. | Vel. mol. de 2000 yardas por segundo [1,8 km/s]. | Vel. mol. de 3000 yardas por segundo [2,7 km/s]. |
|---|---|---|---|---|
| 10-29 | 25.000.000 | 200.000.000 | 1.500.000.000 | 5.000.000.000 |
| 10-30 | 62.500.000 | 500.000.000 | 4.000.000.000 | 13.000.000.000 |
| 1,5 x l0-31 | 100.000.000 | 1.300.000.000 | 10.000.000.000 | 30.000.000.000 |
Todas las estrellas conocidas tienen un peso comparable al del sol. Por lo tanto, si, como conjeturó Newton, las estrellas aparecieron primero como condensaciones de este tipo, entonces las entradas en esta tabla deberían ser comparables con la unidad. La conjetura de Newton, en la forma en que la acabamos de considerar, es claramente insostenible, ya que todos los pesos calculados son muchos millones de veces el del sol. Si alguna vez existió un caos primitivo del tipo que ahora estamos considerando, no se condensaría en estrellas, sino en condensaciones enormemente más masivas, cada una con el peso de millones de estrellas.
[ p. 204 ]
¶ El nacimiento de las grandes nebulosas
Ahora bien, es significativo que se conozcan cuerpos en el espacio que tienen pesos iguales a los que acabamos de calcular, a saber, las grandes nebulosas extragalácticas. Hay dos nebulosas cuyos pesos se pueden determinar con bastante precisión, a saber, la Gran Nebulosa en Andrómeda (Lámina IV, p. 30) y la nebulosa NGC 4594 en Virgo (Lámina XV). Hubble estima que estos son los siguientes:
| Nebulosa | Peso |
|---|---|
| Nebulosa M 31 | peso = 3500 millones de veces el del sol |
| Nebulosa NGC 4594 | „ = 2000 |
De nuevo, estas estimaciones son probablemente bajas, pero su orden general de magnitud es tal que sugiere que las condensaciones que se formarían primero a partir de la nebulosa primigenia deben haber sido las grandes nebulosas extragalácticas, y no meras estrellas. Por supuesto, en el mejor de los casos, es solo una conjetura que las grandes nebulosas se formaron de esta manera, aunque no sea por otra razón porque nunca podemos saber si la hipotética nebulosa primigenia siquiera existió, pero parece la hipótesis más razonable que podemos formular para explicar el hecho de que las nebulosas actuales existen. Estas nebulosas son generalmente tan similares entre sí que parece probable que todas hayan sido producidas por la acción del mismo agente, y lo que acabamos de considerar proporciona una explicación razonable que, aparte de la existencia postulada de la nebulosa primigenia continua, se basa en verae causae.
Las grandes nebulosas, por supuesto, no son exactamente similares, y nuestra próxima investigación debe ser sobre el origen de sus diferencias.
Si las condensaciones en la nebulosa gaseosa primigenia [ p. 205 ] se hubieran formado y contraído de manera absolutamente regular, el producto final sería un conjunto de masas de gas perfectamente iguales y similares espaciadas con perfecta regularidad. Pero la naturaleza rara vez es tan regular como esto; y no debemos sorprendernos de que el conjunto de nebulosas observado no esté espaciado uniformemente, o que sus miembros no tengan el mismo peso ni estén dispuestos simétricamente. A medida que se contrajeron las condensaciones originales en el gas primitivo, debieron de producir corrientes, y es poco probable que estas ocurrieran de manera absolutamente simétrica. Si el movimiento de cada masa de gas en condensación hubiera sido directamente hacia el centro de la condensación en cada punto, el resultado final habría sido una nebulosa esférica desprovista de todo movimiento, pero cualquier sistema de corrientes menos simétrico daría como resultado un giro dado a cada masa que se contrae. Sin duda, este giro sería muy lento al principio, pero el conocido principio de «conservación del momento angular» requiere que, a medida que un cuerpo giratorio se contrae, su velocidad de giro debe aumentar. Así, cuando se completaba el proceso de condensación, el producto final sería una serie de nebulosas que giraban a diferentes velocidades.

Nebulosa su rotación. Y esto es exactamente lo que se observa; en lo que respecta a nuestra evidencia, las nebulosas están en rotación y a diferentes velocidades. Las diversas partes de la superficie de cualquier masa giratoria necesariamente tienen diferentes velocidades en el espacio. El sol, por ejemplo, gira alrededor de su eje en tal dirección que la superficie que vemos se mueve siempre de este a oeste; como resultado, el limbo oriental siempre avanza hacia la tierra, mientras que el limbo occidental se aleja de nosotros. Un espectroscopio dirigido a diferentes partes de la superficie del sol en sucesión revela inmediatamente estas diferencias de velocidad; no solo nos aseguran la rotación del sol, [ p. 206 ] sino que nos permite medir su cantidad. Las nebulosas pueden ser examinadas de la misma manera, y el examen muestra que un gran número de ellas están girando con el movimiento perfectamente regular de un cuerpo sólido, una peonza, por ejemplo. Medido por los estándares terrestres, sus velocidades de rotación parecen extraordinariamente lentas; por ejemplo, la Gran Nebulosa M 31 de Andrómeda requiere unos 19.000.000 de años para realizar una rotación completa, pero esta aparente lentitud es el resultado inevitable del enorme tamaño de la nebulosa. Incluso para dar la vuelta una vez cada 19.000.000 de años, las partes exteriores de la nebulosa tienen que moverse a velocidades de cientos de kilómetros por segundo.
Algunas de las nebulosas tienen formas bastante irregulares, pero la mayoría tienen formas regulares, y es muy significativo que estas son precisamente las formas que, puede calcularse matemáticamente, exhibirían las masas de gas en rotación. En realidad, hay un caso mucho más sólido que éste para suponer que las nebulosas son masas de gas en rotación. A partir de la evidencia puramente observacional del brillo de la superficie y otras características, Hubble descubrió que casi todas estas nebulosas se podían organizar en una única secuencia lineal: se podían organizar en orden como cuentas en un hilo. Y este orden resultó ser prácticamente idéntico a la secuencia que se había calculado previamente, por métodos puramente teóricos, para las configuraciones de masas de gas que giraban a velocidades gradualmente crecientes.
Examinemos esta secuencia de configuraciones teóricas en su orden natural.
Una masa de gas que no girara en absoluto asumiría, por supuesto, una forma esférica bajo su propia gravitación. Varias nebulosas perfectamente esféricas son [ p. 207 ] conocidas; un ejemplo típico se muestra en la fig. 1 en la lámina XVI.

Con una ligera rotación, la masa asume la forma de una naranja ligeramente aplanada, como la Tierra o Júpiter. También se conocen en abundancia nebulosas de esta forma; se muestra un ejemplo en la fig. 2 en la misma lámina.
Con un mayor grado de rotación, el grado de aplanamiento aumenta, pero el cálculo teórico muestra que pronto se abandona la forma de naranja. El ecuador primero comienza a mostrar una protuberancia pronunciada, hasta que finalmente, con suficiente rotación, se convierte en un borde afilado, la masa giratoria ahora tiene la forma de una lente doblemente convexa. Esta predicción de la teoría es abundantemente confirmada por la observación, ya que se observa un gran número de estas nebulosas en forma de lente en el cielo. Un ejemplo se muestra en la fig. 3 en la lámina XVI.
El siguiente paso es algo sensacional. La rotación adicional no da como resultado, como podría esperarse, un aplanamiento aún mayor. Hasta ahora, cada aumento en la rotación ha hecho que la protuberancia en el ecuador sea más pronunciada, pero ahora es tan pronunciada como puede ser. La teoría muestra que el aplanamiento también ha llegado al límite máximo posible, y que la siguiente etapa debe consistir en que la materia sea expulsada a través del borde agudo del ecuador y se extienda por todo el plano ecuatorial. Aquí nuevamente la observación confirma la teoría; las figuras 4 y 5 (Lámina XVI) muestran tipos de nebulosas realmente observadas, siendo la primera la nebulosa en Virgo que ya hemos discutido.
La capa comparativamente delgada de gas que ahora se encuentra en el plano ecuatorial es similar en un aspecto al menos a la materia de Newton «dispuesta uniformemente en un espacio infinito». Las perturbaciones se pueden configurar en él de varias maneras, y cualquier perturbación, sin importar cuán [ p. 208 ] leve, debe dar lugar a la creación de una serie de condensaciones. Como antes, los que están por debajo de cierto límite de tamaño desaparecen por sí mismos, mientras que los que están por encima de este límite aumentan continuamente en intensidad hasta haber absorbido todo el gas en el plano ecuatorial. Nuevamente, como con el hipotético caos primigenio, podemos calcular el tamaño mínimo de condensación que se puede esperar que tenga una existencia permanente, y una vez más el resultado demuestra ser muy significativo.
Ya se han dado las estimaciones de Hubble de los pesos totales de dos nebulosas visibles. Como se conocen las distancias, y por lo tanto también los tamaños, de ambas nebulosas, es fácil calcular la densidad media del gas en toda la nebulosa. Se encuentra que la densidad promedio en M 31 es aproximadamente 5 x 10-22 de la del agua; el número correspondiente a NGC 4594 es 2 x 10-21. Estas cifras nos dan una idea de la densidad de la materia en las regiones exteriores de las nebulosas. Aunque estas densidades son alrededor de mil millones de veces mayores que la densidad estimada de la nebulosa primigenia original del espacio, siguen siendo casi inconcebiblemente bajas. Todavía hay solo una molécula por pulgada cúbica, y una sola respiración de los pulmones de una mosca podría llenar una gran catedral con aire de esta densidad.
Al proceder a calcular los pesos de las más pequeñas condensaciones que se pueden formar y persistir en un gas de esta baja densidad, se obtienen los resultados que se muestran en la siguiente tabla. Las velocidades moleculares se toman bastante bajas, para permitir el enfriamiento que debe ocurrir cuando el gas se esparce en el plano ecuatorial de la nebulosa.
Nuevamente, los pesos de las condensaciones se dan en términos del peso del sol. Y el hecho significativo [ p. 209 ] surge de que la mayoría de las entradas en la tabla representan pesos comparables con el del sol. Estamos lidiando con pesos estelares por fin; las condensaciones que deben formarse en las regiones exteriores de las grandes nebulosas tendrán pesos comparables a los de las estrellas.
| Densidad en términos de agua | Vel. mol. de 100 yardas por segundo [91 m/s]. | Vel. mol. de 300 yardas por segundo [274 m/s]. | Vel. mol. de 500 yardas por segundo [457 m/s]. |
|---|---|---|---|
| 10-21 | 1,7 | 36 | 220 |
| 10-22 | 5 | 130 | 625 |
| l0-23 | 17 | 360 | 2200 |
¶ El nacimiento de las estrellas
Y, de hecho, puede haber pocas dudas de que el proceso que acabamos de considerar es el del nacimiento de las estrellas. Incluso una mirada casual a las fotografías de las nebulosas es suficiente para mostrar que la materia que ha sido expulsada al plano ecuatorial de una nebulosa no se encuentra distribuida uniformemente en ese plano; se ve que ha caído en racimos, nudos o condensaciones. Estos son bastante evidentes en muchas de las fotografías de nebulosas ya mostradas, pero se pueden ver aún más claramente en las nebulosas que se ven casi de frente, como por ejemplo las dos llamativas nebulosas que se muestran en las Láminas XVII y XVIII.
Estos racimos son invariablemente demasiado grandes para ser interpretados como estrellas individuales; son más probablemente grupos de estrellas. En los telescopios más grandes se descomponen en un gran número de puntos de luz en la forma ya expuesta en la Lámina XI (p. 70). Ya hemos mencionado las razones que nos obligan a considerar estos puntos de luz como estrellas reales, siendo la principal que algunos de ellos muestran las fluctuaciones de luz características [ p. 210 ] de las variables Cefeidas. No está del todo claro si las estrellas se forman directamente como condensaciones en el plano ecuatorial de la nebulosa, o si se forman primero condensaciones más grandes, a saber, los racimos observables en fotografías de nebulosas, que posteriormente forman condensaciones más pequeñas, las estrellas. En general, parece probable que haya dos procesos involucrados: primero, la descomposición de la materia nebular en grandes condensaciones, y luego la ruptura de estas grandes condensaciones en estrellas. Tal sucesión de procesos bien podría acompañar un enfriamiento gradual de la materia y, por supuesto, es posible que haya incluso más de dos procesos involucrados. No hay necesidad de formarse una opinión final sobre esto en este momento, ya que no es de ninguna manera esencial para el progreso del argumento principal.
Una colección de fotografías de nebulosas nos permite seguir la evolución nebular desde las etapas más tempranas que se muestran en la Lámina XVI (p. 207), hasta la primera aparición de racimos granulares, como se muestra en la Lámina XVII, y la primera aparición distinta de estrellas que se muestra en Lámina XVIII, hasta las últimas etapas, como se muestra en las Láminas XIX y XX, en las que la nebulosa parece ser poco más que una nube de estrellas. Hubble ha descubierto que es posible seguir la secuencia aún más, y puede trazar una transición continua desde las nebulosas de este último tipo hasta nubes de estrellas puras como las Nubes de Magallanes Mayor y Menor que se muestran en la Lámina XXI.
Así, las estrellas parecen haber nacido de la misma manera que hemos conjeturado que sus padres, las grandes nebulosas, habían nacido antes que ellas, es decir, por medio de lo que generalmente se conoce como «inestabilidad gravitacional». Esto hace que cualquier masa de gas caótico se rompa en condensaciones separadas, [ p. 211 ] y, cuanto más tenue sea el gas original, mayor será el peso de las condensaciones formadas a partir de él. La nebulosa primigenia original era de tan baja densidad que las condensaciones que se formaban en ella pesaban miles de millones de veces más que el sol. Estos aumentaron tanto su densidad al contraerse que cuando su rotación hizo que expulsaran materia gaseosa, esto se condensó en masas de peso estelar que creemos que en realidad son estrellas.


Tenemos un conocimiento menos cierto del primer proceso que del segundo. Nuestra única razón para pensar que el proceso anterior ocurrió alguna vez es que las nebulosas extragalácticas ahora existen. No hay evidencia de que la nebulosa caótica primigenia haya existido alguna vez, más allá del hecho de que la hipótesis de su existencia previa lleva a una explicación muy satisfactoria de que las nebulosas actuales existen tal como lo hacen ahora. Por otro lado, no sólo sabemos que existen las estrellas: también sabemos que existen las masas de gas de las cuales la teoría muestra que las estrellas necesariamente deben nacer. Son las tenues franjas ecuatoriales de las grandes nebulosas. Nuestros telescopios nos muestran tanto las franjas nebulares como las estrellas, y casi podemos estudiar el proceso real del nacimiento.
El Sistema Galáctico de Estrellas. Si este es el verdadero relato del nacimiento de las estrellas, entonces nuestro sol y sus compañeros en el espacio deben haber nacido de una nebulosa giratoria. La observación da un fuerte apoyo a esta conclusión. Desde la época de los Herschel, se ha comentado con frecuencia que el sistema galáctico tiene la forma general de las nebulosas extragalácticas, representando el plano galáctico, por supuesto, el plano ecuatorial de la nebulosa original. En términos puramente observacionales, el pensamiento astronómico actual se está moviendo rápidamente hacia [ p. 212 ] todo el sistema galáctico, ya sea como una nebulosa giratoria o como restos de una. Incluso es posible que esto aún conserve una región central que aún no está condensada en estrellas.
En 1904, Kapteyn descubrió que las direcciones de movimiento de las estrellas en la vecindad del sol no estaban distribuidas al azar. Las estrellas parecían preferir moverse de un lado a otro a lo largo de una dirección determinada en el plano galáctico en lugar de en otras direcciones: «flujo de estrellas», lo llamó. Se puede esperar que esta peculiaridad en el movimiento de las estrellas arroje alguna luz sobre su origen.
Cada estrella se mueve en una órbita complicada bajo la atracción gravitatoria de todas las demás estrellas del sistema galáctico. No es posible calcular esta órbita en detalle. La órbita de un planeta alrededor del sol se calcula fácilmente porque sólo intervienen dos cuerpos, el planeta y el sol. Pero incluso cuando solo hay tres cuerpos involucrados, es imposible calcular las órbitas que cada uno describe bajo las atracciones de los otros dos juntos: este es el famoso problema de los tres cuerpos, que nunca se ha resuelto. Cuando, como en el sistema galáctico, están involucrados miles de millones de estrellas, es naturalmente inútil tratar de calcular la órbita de cada estrella; sería tan fútil como tratar de calcular la trayectoria de cada molécula en un gas.
Sin embargo, los mismos métodos estadísticos que nos dan información útil sobre las propiedades de un gas pueden aplicarse al estudio de los movimientos de las estrellas. Hay tantas estrellas que no nos preocupamos por los individuos en absoluto, simplemente los tratamos a todos juntos como una multitud. Para [ p. 213 ] tratarlos como individuos sería como si la compañía ferroviaria tratara de pronosticar el tráfico de Bank Holiday de Londres a Brighton considerando las finanzas, los hábitos y la psicología de cada londinense individual.


Sin entrar en detalles individuales, podemos ver que cada estrella debe describir una órbita que, después de recorrer gran parte de la galaxia, regresa a algún punto cercano a su punto de partida. Los cálculos muestran que cada uno de esos circuitos debe tardar cientos de millones de años en completarse. Aun así, las estrellas en su mayoría habrán realizado varios circuitos completos mientras la tierra ha existido, y si tenemos razón al suponer que las edades de las estrellas son millones de millones de años, cada estrella debe haber dado la vuelta a la galaxia varios miles de veces. En consecuencia, deberíamos esperar que la galaxia ya haya asumido una forma definitiva y permanente; la distribución de las estrellas en sus diferentes partes debería haberse convertido en algo así como constante, y las estrellas deberían haberse establecido en un estado aproximado a uno de movimiento constante.
Los métodos estadísticos de investigación muestran que no hay un gran número de arreglos posibles para un sistema de estrellas que haya vivido lo suficiente como para alcanzar un estado estable. Si el sistema como un todo no tiene ninguna rotación, solo hay un arreglo; las estrellas forman una masa globular con perfecta simetría en todas las direcciones. Los cúmulos globulares observados (Lámina IX, p. 63) proporcionan buenas aproximaciones a este tipo de formación, aunque Shapley ha descubierto que la mayoría no tienen una forma absolutamente esférica. Si el sistema en su conjunto está dotado de rotación, las configuraciones posibles son todas de forma simétrica aplanada, como una moneda, un reloj o una galleta redonda; en otras [ pags. 214] palabras, un sistema de estrellas en rotación debe tener una forma similar a la que creemos que tiene la galaxia. Además, los movimientos de estas estrellas deben mostrar un «flujo estelar» precisamente del tipo descubierto por Kapteyn.

Así, tanto la forma de la galaxia como las peculiaridades del movimiento de sus estrellas indican que el sistema galáctico en su conjunto debe estar en estado de rotación. Y, como hemos visto (p. 67), investigaciones observacionales recientes de Oort, Plaskett y otros aseguran con bastante certeza que la rotación requerida por la teoría es un hecho real. Los movimientos de las estrellas indican que todo el sistema galáctico gira a un ritmo que varía de una región a otra, aproximadamente una revolución cada 230 millones de años en la vecindad del sol. Y se encuentra que el centro de esta gigantesca rueda coincide muy de cerca con el lugar que Shapley había fijado previamente como el centro geométrico del sistema galáctico a partir de sus investigaciones sobre la distribución de los cúmulos globulares.
Así, como la rotación no puede generarse de la nada, todos los fenómenos concuerdan en mostrar que el sistema galáctico debió nacer de un cuerpo en rotación. Estamos familiarizados con un solo tipo de cuerpo astronómico que es de tamaño suficiente para convertirse en un sistema galáctico, a saber, las grandes nebulosas, y como se cree que la mayoría de ellos, y algunos se sabe con certeza, están en rotación, parece razonable concluir que el sistema galáctico debe haber nacido de una nebulosa, a menos que su estructura sea todavía tal que debería describirlo incluso ahora como una nebulosa si lo viéramos desde la gran distancia desde la que vemos las otras grandes nebulosas. El período de rotación observado del sistema galáctico, del orden de 230 millones de años, es [ p. 215 ] sustancialmente más largo que el período, ya sea conocido o sospechado, de cualquiera de las nebulosas, pero las dimensiones del sistema galáctico también son mayores que las de cualquier nebulosa conocida, y los dos hechos están relacionados. Nuevamente, la cantidad de estrellas en el sistema galáctico es probablemente sustancialmente mayor que en cualquier nebulosa, al igual que el peso total de estas estrellas[2]. Todo esto deja en claro que si la galaxia es, o alguna vez ha sido, una de las grandes nebulosas, debe haber sido una de tamaño y peso inusuales.
Hemos visto cómo el sol y todas las estrellas pierden peso continuamente como resultado de su emisión de radiación. De ello se deduce que el peso total del sistema galáctico está disminuyendo constantemente y, como consecuencia, su control gravitacional sobre sus estrellas constituyentes se está debilitando continuamente. Si este control gravitacional desapareciera repentinamente por completo, cada estrella reemplazaría su trayectoria curva actual por una línea perfectamente recta, a lo largo de la cual viajaría a su velocidad actual, sin ser desviada por las fuerzas gravitatorias de otras estrellas, de modo que las estrellas que ahora constituyen el sistema galáctico pronto se dispersaría por todo el espacio. En resumen, si la atracción gravitatoria de las estrellas se aboliera repentinamente, la galaxia comenzaría a expandirse a gran velocidad.
Aunque no es probable que esto suceda, la abolición gradual de la atracción gravitatoria de las estrellas, a medida que convierten su peso en radiación, debe hacer que la galaxia se expanda todo el tiempo a un ritmo lento: los cálculos sugieren que su ritmo actual de expansión sería duplicar su tamaño en unos 30 millones de millones de años. La expansión [ p. 216 ] debe haber sido mucho más rápida en el pasado, cuando las estrellas estaban llenas de vigor juvenil y despilfarraban su sustancia más abundantemente que ahora, por lo que parece probable que el sistema galáctico era sustancialmente más pequeño y más compacto en el pasado que ahora, y la nebulosa original probablemente aún más pequeña.
Hemos visto cómo las estrellas de las grandes nebulosas parecen estar congregadas en racimos o cúmulos. Los cúmulos globulares del sistema galáctico posiblemente sean grupos de estrellas del mismo tipo general, que no han sido perturbadas por otros grupos de estrellas y, por lo tanto, han asumido la forma globular bajo su propia atracción, tal como lo haría una masa de gas. Shapley encuentra que estos cúmulos se encuentran algo fuera del plano galáctico; parece como si estuvieran fragmentados o desorganizados al viajar a través de este plano, donde se encontrarían con otras estrellas.
Por el contrario, los grupos de estrellas del tipo generalmente descrito como cúmulos en movimiento (las Pléyades, las Hyades, las estrellas de la Osa Mayor y una multitud de otras que viajan en compañía de ellas por el espacio) generalmente se encuentran moviéndose en el plano galáctico. Es muy posible que estos representen los vestigios finales de cúmulos globulares que se han roto por la interacción con otras estrellas, todos excepto los miembros más masivos que han sido eliminados de la formación. El análisis matemático muestra que la interacción entre las estrellas de tales cúmulos en movimiento y otras estrellas en el plano galáctico haría que cada cúmulo asumiera la forma de una galleta plana o un reloj, de diámetro igual a 2 ½ veces su espesor. Es significativo que la mayoría de los cúmulos en movimiento presenten un aplanamiento de este tipo, su importe concordando bastante bien con el valor calculado. Incluso es concebible que el [ p. 217 ] «cúmulo local» que rodea al sol (p. 65) pueden ser los restos de ese grupo de estrellas.
Los movimientos de estos cúmulos también pueden inducir un mayor aplanamiento, en una dirección perpendicular a su movimiento. Algunos cúmulos muestran este aplanamiento adicional, siendo el cúmulo de la Osa Mayor un ejemplo llamativo.
¶ El nacimiento de los sistemas binarios
Al discutir la forma en que las nebulosas podrían nacer del caos, notamos que la existencia de corrientes en el medio primordial dotaría a las nebulosas resultantes de grados variables de rotación. Por la misma razón, los hijos de las nebulosas, las estrellas, también deben estar dotados de rotación en su nacimiento. Hay otra razón para tal rotación. El principio general de la «conservación del momento angular» requiere que la rotación, como la energía, no pueda desaparecer por completo. Su cantidad total se conserva, de modo que cuando una nebulosa se rompe en estrellas, la rotación original de la nebulosa debe conservarse en las rotaciones de las estrellas. Así, las estrellas, tan pronto como nacen, están dotadas de rotaciones que les transmite su nebulosa madre, además de las rotaciones resultantes de las corrientes establecidas en el proceso de condensación.
Su continua pérdida de peso hace que cambien las condiciones físicas de las estrellas, y en el próximo capítulo veremos que este cambio generalmente implica una reducción del diámetro de la estrella. El mismo principio de «conservación del momento angular» ahora requiere que, a medida que una estrella se encoge, su velocidad de rotación debe aumentar. En resumen, a medida que una estrella envejece, gira cada vez más rápido.
[ p. 218 ] Ahora bien, la rotación fue el factor esencial en el nacimiento de las estrellas a partir de la nebulosa madre. Una nebulosa totalmente desprovista de rotación no se rompería en estrellas, hasta donde podemos ver, y esta predicción de la teoría parece ser confirmada por la observación, ya que las nebulosas del tipo perfectamente esférico que se muestra en la fig. 1 de la Lámina XVI nunca se puede resolver en estrellas en el telescopio. Por otro lado, vimos cómo las nebulosas que inicialmente estaban dotadas de rotación aumentaban continuamente su velocidad de rotación al contraerse, hasta que finalmente su rotación las dividía y producía una familia de estrellas a partir de cada una. Obviamente, ahora surge la pregunta de si, a medida que aumenta la velocidad de rotación de las estrellas, es probable que estas se rompan a su vez, y producir aún una tercera generación de cuerpos astronómicos. Una vez más, podríamos esperar que el análisis matemático se aplicara por igual a cuerpos grandes y pequeños, independientemente de la escala. Y un examen detallado del problema muestra que, de hecho, el proceso que hemos tenido bajo consideración se repetiría y de nuevo traería a la existencia una nueva generación de cuerpos más pequeños, siempre que las condiciones físicas fueran adecuadas.
Las condiciones físicas, sin embargo, resultan no ser las adecuadas; ciertamente fallan en un aspecto al menos. Aunque una estrella en rotación puede expulsar materia gaseosa en su plano ecuatorial, todo el proceso será a una escala mucho menor que en las nebulosas. Podríamos esperar que la materia expulsada forme condensaciones como antes, pero los cálculos muestran que, a menos que la velocidad molecular sea extraordinariamente baja, ¡ninguna condensación puede sobrevivir a menos que tenga un peso mayor que el peso total de la estrella! Esto significa que con cualquier velocidad molecular razonable, el gas expulsado no [ p. 219 ] forma condensaciones. Simplemente se dispersaría en el espacio circundante, formando una atmósfera sin condensaciones distintas.
Tal es el curso de los acontecimientos si las estrellas, como las nebulosas antes que ellas, son tratadas como masas puras de gas. Sin embargo, debe considerarse otra alternativa.
La fisión de estrellas líquidas. Hemos visto cómo una nebulosa gaseosa sin rotación asumiría una forma estrictamente esférica bajo su propia atracción gravitatoria, mientras que una ligera rotación haría que se aplanara hasta adoptar una forma de naranja, como la Tierra. La tierra también ha asumido esta forma a causa de su rotación, aunque su estructura interna es muy diferente a la de una nebulosa gaseosa.
Una estricta investigación matemática muestra que esta forma aplanada de color naranja debe ser común a todos los cuerpos que giran lentamente, independientemente de su composición interna; los gases, los líquidos y los cuerpos plásticos lo asumen por igual. Pero la forma de un cuerpo que gira rápidamente debe depender en gran medida de su disposición interna y constitución, viéndose especialmente afectada por la medida en que el peso del cuerpo se concentra cerca de su centro.
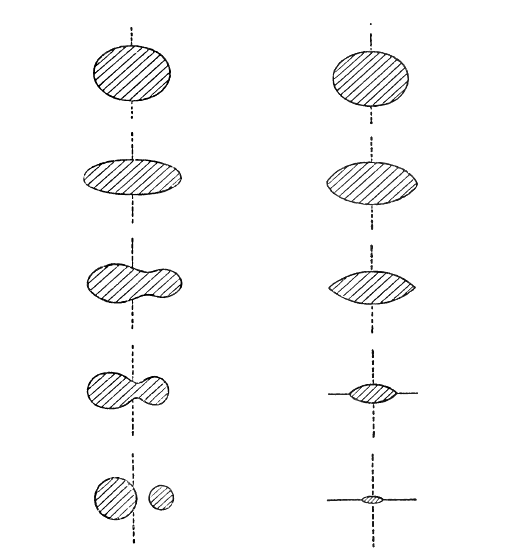
Como consecuencia de la alta compresibilidad de los gases, esta concentración central de peso alcanza su límite extremo en una masa puramente gaseosa. El extremo opuesto se alcanza en una masa de líquido uniforme e incompresible como el agua, en la que no puede haber concentración central alguna. A medida que una masa de este último tipo aumenta su velocidad de rotación, la forma de naranja ligeramente aplanada simplemente da lugar a la forma de una naranja más aplanada. La tendencia de una masa gaseosa a formar un borde afilado alrededor del ecuador está completamente ausente, y la sección transversal de su figura sigue siendo [ p. 220 ] elíptica en toda su extensión. A una velocidad de rotación aún mayor, el ecuador pierde su forma circular y también se vuelve elíptico. La figura tiene ahora tres diámetros desiguales, pero cada sección transversal es estrictamente elíptica; la figura es un «elipsoide». Después de esto, su diámetro mayor comienza a alargarse hasta que la masa, aún de forma elipsoidal, ha formado una figura en forma de cigarro con una longitud de casi tres veces su diámetro menor.
Ahora comienza una nueva serie de eventos. La masa de líquido se concentra gradualmente alrededor de dos puntos distintos en su diámetro más largo, formándose una cintura o surco en su centro. Este surco se hace más y más profundo hasta que ha cortado el cuerpo en dos masas separadas distintas, que ahora giran en movimiento orbital una alrededor de la otra y forman una estrella binaria. La secuencia de eventos se muestra en la fig. 11; ya se han dado diagramas de la etapa final representada por estrellas binarias reales en la p. 54.
A modo de comparación, la secuencia de formas asumidas por una masa de gas en rotación se muestra en la fig. 12, siendo esto idéntico a la secuencia de formas nebulosas observadas que en realidad se observa, y se ilustra fotográficamente en la Lámina XVI (p. 207).
Las dos cadenas de configuraciones mostradas en las figs. 11 y 12 representan, se recordará, los dos casos extremos de un cuerpo giratorio cuya sustancia se distribuye con completa uniformidad, y de un cuerpo giratorio cuya sustancia está muy condensada hacia su centro. Como las constituciones de los cuerpos astronómicos reales deben estar en algún lugar entre estos dos extremos, naturalmente podríamos esperar que tal cuerpo siga una serie de configuraciones intermedias entre las dos mostradas en las figs. 11 y 12. La teoría muestra que, de hecho, no es así. Todos los cuerpos que tengan menos de un cierto [ p. 221 ] grado crítico de condensación central sigue la secuencia que se muestra en la fig. 11, o una secuencia que difiera sólo inmaterialmente de ésta; todos los cuerpos que tienen más de esta cantidad crítica de condensación central siguen la secuencia que se muestra en la fig. 12. Así, cuando se alcanza este grado crítico de condensación central, hay un [ p. 222 ] giro repentino desde la fig. 11 a la fig. 12. En resumen, todo cuerpo que gira se comporta como si fuera puramente líquido, o como si fuera puramente gaseoso; no hay posibilidades intermedias.
La astronomía observacional no deja lugar a dudas de que un gran número de estrellas, posiblemente incluso todas las estrellas, siguen la secuencia mostrada en la fig. 11. Hasta donde sabemos, no se dispone de ningún otro mecanismo para la formación de los numerosos sistemas binarios espectroscópicos, en los que dos constituyentes describen pequeñas órbitas entre sí. En estas estrellas, entonces, la condensación central de masa debe estar por debajo de la cantidad crítica que acabamos de mencionar; en esta medida se comportan como líquidos más que como gases.
Nos hemos basado enteramente en el análisis matemático para rastrear los detalles del proceso de fisión que acabamos de describir. Y somos totalmente incapaces de comprobar nuestros resultados teóricos mediante la observación. No hay una sola estrella en el cielo de la que podamos decir: aquí hay una estrella que ciertamente ha comenzado a romperse por fisión, y seguramente terminará como un sistema binario. Quizás no sea del todo sorprendente. El proceso de ruptura es con toda probabilidad de muy corta duración en comparación con la vida de las estrellas, de modo que en cualquier caso deberíamos investigar muchas estrellas antes de atrapar una en el acto de romperse en dos.
Por otro lado, una estrella en el acto de romperse debería ser muy fácil de diferenciar de las estrellas ordinarias. El análisis matemático muestra que su interior estaría en un estado de agitación considerable, por lo que difícilmente podría brillar con una luz constante: sería una estrella «variable». Además, su condición debería mostrar un cambio progresivo, aunque es una pregunta abierta si esto sería lo suficientemente rápido como para [ p. 223 ] detectarse en unos pocos años de observación. Finalmente, si se sospechara que algún grupo o clase de estrellas son estrellas en proceso de fisión, debería ser posible ordenarlas en un orden correspondiente al grado en que el proceso de fisión había avanzado, y la secuencia así formada debería terminar con estrellas en la condición física de binarias recién formadas.
Recientemente he sugerido que las variables cefeidas, cuyo mecanismo desconocido de variación de la luz presta un servicio tan valioso al astrónomo, son simplemente estrellas en el acto de fisión. La falta de espacio nos impide entrar aquí en la intrincada cuestión de hasta qué punto exhiben las peculiaridades que el análisis matemático requiere de las estrellas en proceso de fisión, pero se ve fácilmente que satisfacen las tres pruebas simples esbozadas anteriormente. Ciertamente son estrellas variables, y las variaciones de luz de diferentes estrellas son tan similares que sugieren fuertemente que todas surgen por la misma causa. Se sospecha que los períodos de varias Cefeidas han cambiado, y Hertzsprung ha estimado que la estrella prototipo, δ Cephei, que ahora se ha observado durante 126 años, está disminuyendo su período de fluctuación de la luz a razón de una décima de segundo por año; por tanto, un millón de años reduciría su período actual de 5⅓ días en más de un día. Finalmente, el Dr. Otto Struve descubrió que la secuencia de Cefeidas encaja casi perfectamente con la de las binarias recién formados. Por lo tanto, las perspectivas de la «teoría de la fisión» de las variables cefeidas parecen esperanzadoras, pero la teoría debe probarse muy a fondo antes de que pueda aceptarse, y no se puede afirmar que hasta ahora haya sido probada a fondo o aceptada ampliamente.
Una visión alternativa, propuesta por primera vez por Plummer y Shapley, considera a las variables cefeidas como pulsantes [ p. 224 ] esferas de gas. El comportamiento de tales masas de gas ha sido investigado matemáticamente por Eddington y otros, pero no parece que pueda reconciliarse con el comportamiento observado de las variables Cefeidas.
¶ El desarrollo de sistemas binarios
Cualquiera que sea el proceso de formación de los sistemas binarios, experimentamos un camino bastante sencillo al intentar rastrear el desarrollo subsiguiente de tales sistemas. Tres factores están simultáneamente en operación.
Fricción de marea. El primero de estos tres factores, que es sólo de breve duración, fue designado «fricción de marea» por Sir George Darwin, quien primero llamó la atención sobre él e investigó la forma en que operaba. Cuando por primera vez una masa en rotación se rompe y forma un sistema binario, los dos componentes están tan cerca que necesariamente provocan tremendas mareas entre sí; Darwin demostró que estos separan los dos cuerpos e igualan sus velocidades de rotación al hacerlo. Después de que estos procesos hayan estado en funcionamiento durante millones de años, las velocidades de rotación de los dos cuerpos y su velocidad de revolución entre sí deben volverse iguales, de modo que cada cuerpo gire perpetuamente la misma cara hacia su compañero, y los dos giren. uno alrededor del otro como las dos masas de una mancuerna unidas por un brazo invisible.
Aunque un sol y un planeta no forman un sistema binario en el sentido técnico estricto, están necesariamente sujetos a las mismas fuerzas que los verdaderos sistemas binarios. Así podemos ver la operación de la fricción de las mareas en el hecho de que Mercurio siempre da la misma cara al sol, y que Venus gira tan lentamente sobre su eje que [ p. 225 ] da la misma cara al sol día tras día, y probablemente también semana tras semana. A medida que avanzamos en el espacio, los efectos de la fricción de las mareas disminuyen rápidamente, pero probablemente sea significativo que los planetas más cercanos, la Tierra y Marte, tengan días de unas 24 horas cada uno, mientras que los planetas remotos Júpiter, Saturno y Urano tienen días de solo unas 10 horas. Se desconocen los períodos de rotación de Neptuno y Plutón.
De la misma manera, la fricción de las mareas ha sido, con toda probabilidad, la principal responsable de la configuración actual del sistema tierra-luna, alejando a la luna hasta su distancia actual de la tierra y haciendo que siempre vuelva la misma cara hacia nosotros. Por supuesto, la fricción de las mareas aún debe estar en funcionamiento. La luna es responsable de la mayor parte de las mareas que se levantan en los océanos de la tierra; estos, ejerciendo un tirón sobre la tierra sólida que se encuentra debajo, disminuyen su velocidad de rotación, con el resultado de que el día se alarga continuamente, y continuará haciéndolo hasta que la tierra y la luna giren y giren al unísono completo. Cuando, si alguna vez, llega ese momento, la tierra volverá continuamente la misma cara hacia la luna, de modo que los habitantes de uno de los hemisferios de la tierra nunca verán la luna en absoluto, mientras que el otro lado será iluminado por él todas las noches. En ese momento, la duración del día y del mes serán idénticas, siendo cada una de ellas aproximadamente 47 de nuestros días actuales. Jeffreys ha calculado que es probable que este estado de cosas se alcance después de unos 50.000 millones de años.
Después de esto, la fricción de las mareas ya no operará en el [ p. 226 ] sentido de alejar a la luna de la tierra. El efecto conjunto de las mareas solares y lunares será ralentizar aún más la rotación de la tierra, y la luna al mismo tiempo disminuirá gradualmente su distancia de la tierra. Cuando finalmente, después de eras impensables, haya sido arrastrado hasta unas 12.000 millas de la tierra, las mareas levantadas por la tierra en el cuerpo sólido de la luna romperán este último en fragmentos (p. 250 abajo), que formarán un sistema de pequeños satélites que girarán alrededor de la tierra de la misma manera que las partículas de los anillos de Saturno giran alrededor de Saturno, o como los asteroides giran alrededor del sol.
Ya hemos notado cómo la disposición actual del sistema tierra-luna nos permite calcular la edad de la tierra; Jeffreys estima que el sistema debe haber tardado algo del orden de 4000 millones de años en alcanzar su configuración actual (p. 155).
Este período, que parece tan largo a juzgar por los estándares terrestres, es solo un momento en la vida de una estrella. Los componentes de la verdadera estrella binaria alcanzan una configuración como la del sistema tierra-luna en una breve fracción de sus vidas y, pasando, alcanzan en el tiempo la configuración en la que cada uno vuelve perpetuamente el mismo rostro hacia el otro. Hasta ahora, la fricción de las mareas ha estado separando cada vez más las masas, pero tan pronto como se alcanza esta etapa, las mareas se vuelven estacionarias en ambos componentes, por lo que la fricción de las mareas deja de funcionar. Así, la separación producida por la fricción de las mareas ha llegado ahora a su límite y, en lo que se refiere a la fricción de las mareas, los dos cuerpos podrían rotar en la forma que acabamos de describir por toda la eternidad.
Pérdida de peso. A medida que la fricción de las mareas se vuelve inoperante, se afianza una nueva agencia. Hemos calculado que el sol está perdiendo peso a razón de [ p. 227 ] 250 millones de toneladas por minuto, que ha estado perdiendo peso a este ritmo, o a un ritmo comparable, durante millones de millones de años, y seguirá haciéndolo durante millones de millones de años por venir. La tierra está a su distancia actual del sol porque esta distancia se adapta exactamente al peso actual del sol. Si el peso del sol se redujera repentinamente a la mitad, su atracción gravitatoria sobre la tierra también se reduciría a la mitad, y la tierra se alejaría más del sol[3].
No es probable que el peso del sol se reduzca repentinamente a la mitad, pero se ha reducido en mil millones de toneladas en los últimos cuatro minutos, con el resultado de que su control gravitatorio sobre la tierra se ha debilitado y la tierra se ha movido hacia afuera a una órbita más amplia; en este momento el radio de la órbita terrestre es mayor que hace cuatro minutos. Los detalles se pueden rastrear matemáticamente con total precisión. Parece que la órbita de la tierra alrededor del sol no es un círculo, ni siquiera una elipse de pequeña excentricidad; es una curva en espiral, como un resorte de reloj desenrollado. Cada año la tierra se mueve un pequeño paso más hacia el frío exterior y la oscuridad; el cálculo exacto muestra que su distancia promedio del sol aumenta a razón de aproximadamente un metro (39,37 pulgadas) por siglo. Por supuesto, el efecto es exactamente del mismo tipo que el que hemos visto que debe producirse en el sistema galáctico por la pérdida de peso de las estrellas. La única diferencia es que en la galaxia se está expandiendo un sistema de miles de millones de estrellas, mientras que el sistema sol-tierra consta de solo dos miembros.
[ p. 228 ] Efectos exactamente similares deben ser producidos por la pérdida de peso en los dos componentes de una estrella binaria. Aquí, ambos componentes irradian energía y, al mismo tiempo, pierden peso. Cálculos detallados muestran que deben alejarse continuamente unos de otros, pero que la forma de su órbita no sufrirá ningún cambio.
Ni por separado ni en combinación, los dos efectos que acabamos de describir explican las formas o los tamaños de las órbitas observadas de las estrellas binarias en su conjunto. Para interpretarlos, debemos recurrir a un tercer agente, las fuerzas gravitatorias de las estrellas que pasan. Ya hemos visto cómo éstos dan cuenta de la distribución estadística de órbitas que realmente se observa.
La combinación de las tres agencias, la fricción de las mareas, que se extiende a lo largo de millones de años, la pérdida de peso, que se extiende a lo largo de millones de millones de años, y la perturbación del paso de las estrellas, que se extiende a lo largo de un período similar, es responsable de la evolución de los sistemas estelares binarios. Su efecto agregado es ampliar la distancia entre las dos estrellas, mientras que al mismo tiempo deforma la órbita.
Subdivisión. Mientras se producen estos cambios en la disposición orbital de un sistema binario, los dos componentes modifican su condición física debido a su continua pérdida de peso y, al igual que con las estrellas madre, esta pérdida de peso generalmente resultará en un encogimiento en el tamaño de la estrella. El encogimiento de cualquiera de los componentes del sistema hace que su forma siga la secuencia de configuraciones que ya hemos enumerado, y si el encogimiento continúa durante el tiempo suficiente, el componente puede terminar dividiéndose aún más en dos masas separadas. [ p. 229 ] Cualquiera de los constituyentes de un sistema binario, o ambos, pueden subdividirse en subsistemas binarios de esta manera, dando como resultado un sistema de tres o cuatro estrellas. H. N. Russell ha demostrado matemáticamente que cuando un sistema binario P, Q se divide en un sistema triple, P, q, q’, al dividirse Q en dos constituyentes q, q’, la distancia entre q y q’ no puede ser mayor que alrededor de un quinto de la distancia original PQ. Esta ley teórica está bien confirmada por la observación. La figura 13 muestra un sistema múltiple típico y observamos que las separaciones en cada uno de los diversos subsistemas son bastante pequeñas en comparación con las de los sistemas principales.

El desarrollo del hipotético caos primitivo ahora se ha rastreado a través de cinco generaciones de cuerpos astronómicos,
caos — nebulosas — estrellas — sistemas binarios — subsistemas,
a la que debe añadirse una sexta generación si las estrellas del subsistema continúan fisionándose, como, por ejemplo, lo han hecho en la estrella que se muestra en la fig. 13. La genealogía de las estrellas comienza con una vasta nebulosa tenue que llena todo el espacio; la última generación consiste en estrellas pequeñas, encogidas y moribundas sin capacidad para una mayor subdivisión. La genealogía ha sido trazada principalmente sobre bases teóricas únicamente, pero no debemos tener dudas en cuanto a su precisión general, ya que la observación la confirma repetidamente y en casi cada paso. De hecho, no es mucho decir que la secuencia evolutiva podría haber sido descubierta [ p. 230 ] casi igualmente bien solo a partir de la evidencia observacional, excepto por el hipotético caos primigenio, sobre el cual, por la naturaleza del caso, la observación no puede tener nada que decir.
¶ El origen del sistema solar
Casi todas las formaciones astronómicas observadas se pueden colocar en la secuencia evolutiva que acabamos de discutir, ya sea con certeza justa o con plausibilidad razonable, a excepción de una excepción destacada y conspicua: el Sistema Solar. La cosmogonía surgió como un intento de descubrir el origen del sistema solar. Las razones por las que limitó sus esfuerzos a este problema en particular son cronológicas; en los primeros días de la cosmogonía, la astronomía apenas era consciente de nada fuera del sistema solar. El esbozo que acabamos de dar de los hallazgos de la cosmogonía científica moderna ha sido notable porque ha exhibido la cosmogonía llevándonos de viaje por todo el universo, explicando el origen y la historia de vida de prácticamente todos los objetos que encontramos en este viaje, y luego quedándonos sin palabras cuando es llevado de vuelta a casa y confrontado con su lugar de nacimiento, el sistema solar.
Hipótesis de la nebulosa de Laplace. La primera cosmogonía científica seria fue la encarnada en la famosa Hipótesis Nebular de Laplace. En 1755, Kant había imaginado un caos primitivo que se condensaba en nebulosas giratorias e, identificando una de estas nebulosas con el sol, había imaginado que los planetas se formarían por la solidificación de masas de gas desprendidas de la nebulosa, de forma muy parecida a como nosotros hemos supuesto que nacen las estrellas. En 1796, Laplace avanzó ideas similares, que desarrolló en detalle con una [ p. 231 ] precisión bastante más allá de las capacidades de Kant. Mostró cómo, a medida que su contracción la hacía girar cada vez más rápido, una masa de gas en rotación se aplanaría y desarrollaría la forma lenticular que ya hemos discutido (fig. 3 de la Lámina XVI), y luego procedería a expulsar materia en su plano ecuatorial, o más bien a dejarla atrás mientras continuaba el encogimiento de la masa principal. En esta etapa se parecería un poco a las nebulosas que se muestran en las figs. 4 y 5 de la Lámina XVI, aunque Laplace, al no estar familiarizado con nebulosas de este tipo, adujo a Saturno rodeado por sus anillos como un ejemplo de la formación que se esperaba en esta etapa (Lámina XXIV, p. 250). Laplace imaginó que la franja de gas abandonado se condensaría y formaría un solo planeta. A medida que la masa principal se encogía más, se abandonaba más gas en el plano ecuatorial, que a su debido tiempo se condensaba en otro planeta, y así sucesivamente, hasta que el sol dejó de encogerse y no nacieron más planetas.
Que la hipótesis es prima facie plausible, es evidente por haber sobrevivido, y de hecho ha sido generalmente aceptada, durante casi un siglo antes de que encontrara una oposición seria. Recientemente se han acumulado críticas, de una naturaleza tan vital como para dejar claro que la hipótesis debe ser abandonada.
El sol, según Laplace, se partió y dio a luz a los planetas por exceso de rotación. Sin embargo, tanto la teoría como la observación indican claramente el destino que le espera a una estrella que gira demasiado rápido para su seguridad; no forma una familia, sino que simplemente estalla, como un volante de inercia, en partes de tamaño casi igual. Los sistemas binarios y múltiples espectroscópicos son reliquias de estrellas que se han desintegrado por un exceso de [ p. 232 ] rotación, y no se parecen en lo más mínimo al sistema solar.
Nuevamente, el principio de «conservación del momento angular» requiere que la rotación del sol primitivo persista en la rotación del sol actual y en las revoluciones de los planetas a su alrededor. Al sumar las contribuciones de todos ellos, obtenemos un total que debería representar el momento angular del sol primitivo. En rigor habría que añadir una contribución más por el peso de toda la radiación que ha emitido el sol desde que nacieron los planetas. Podemos calcular la cantidad de esta contribución, porque conocemos la edad de la tierra con una precisión tolerable, pero resulta ser completamente insignificante.
El momento angular total del sol primitivo se puede calcular con bastante precisión, porque más del 95 por ciento del momento angular total del sistema solar actual reside en el movimiento orbital de Júpiter. Esta contribución puede calcularse con gran exactitud, de modo que alguna incertidumbre en las contribuciones menores que componen el 5 por ciento restante, puede tener poca influencia en el total.
Cuando se calcula este total, surge el sorprendente hecho de que el sol primitivo no pudo haber tenido suficiente rotación para causar la ruptura. Claramente, el sol está muy lejos de ser fragmentado por su rotación actual. El achatamiento de la figura es el primer paso hacia la ruptura, y la figura del sol está tan poco achatada por su rotación actual que hasta ahora las mediciones más refinadas no han podido detectar aplanamiento alguno. Al agregar el momento angular adicional ahora representado en los movimientos de Júpiter y todos los demás miembros del sistema solar, llegamos a un sol primitivo que gira [ p. 233 ] aproximadamente tan rápido como gira Júpiter ahora, y mostrando aproximadamente el mismo grado de aplanamiento de la figura que Júpiter, suficiente para medir con bastante facilidad en un telescopio, o incluso para detectar solo con el ojo, pero nada lo suficientemente como para causar una ruptura.
Es poco probable que el sol haya cambiado mucho desde que nacieron sus planetas, ya que los 2000 millones de años intermedios representan solo una fracción diminuta de la vida total del sol. Sin embargo, si imaginamos que se ha encogido considerablemente en el intervalo, entonces la cantidad disponible de momento angular habría sido aún más incapaz de romper el gran sol primitivo que el actual sol encogido. Se mire como se mire, se llega a la conclusión de que el sol no puede haberse roto, como imaginaba Laplace, por exceso de rotación; de hecho, nunca pudo haber poseído más que una pequeña fracción de la cantidad de rotación necesaria para romperlo.
Una tercera objeción es de carácter algo diferente. Laplace fue un gran matemático, y no había nada malo con su teoría matemática abstracta, hasta donde llegaba. Un análisis moderno más refinado lo ha confirmado a cada paso, y la observación hace lo mismo, como atestiguan las fotografías de nebulosas en rotación (Lámina XVI). Estas fotografías muestran un proceso que tiene lugar ante nuestros ojos, que es esencialmente idéntico al imaginado por Laplace, excepto por una colosal diferencia de escala. Todo sucede cualitativamente como lo imaginó Laplace, pero en una escala incomparablemente mayor de lo que jamás soñó. En estas fotografías, la nebulosa primitiva no es un solo sol en formación, sino que contiene sustancia suficiente para formar cientos de millones de soles; las condensaciones no forman diminutos planetas del tamaño de nuestra tierra, sino que [ p. 234 ] son ellos mismos soles; no son ocho o así en número, sino que deben contarse en millones.
Podemos preguntarnos por qué no puede ocurrir lo mismo en la escala más pequeña imaginada por Laplace, porque ¿no son aplicables las conclusiones de las matemáticas independientemente del tamaño del cuerpo con el que estemos tratando? En efecto, la respuesta ya se ha dado (p. 218). Todo sucede en menor escala según el plan hasta que llegamos a la formación de las condensaciones; aquí la cuestión de la escala resulta vital. Hemos visto (p. 196) cómo las moléculas que forman el sol se han condensado en una estrella a causa de su gran número; las moléculas en una habitación no se condensan en nada porque son muy pocas. De la misma manera, las moléculas dejadas por el lento encogimiento de un sol (suponiendo que este por el momento gire lo suficientemente rápido como para dejar atrás las moléculas) no se condensarían, porque en cualquier instante habría muy pocos de ellos disponibles para la condensación. Se desprenderían por gotas, y una gota de gas no se condensa sino que se dispersa en el espacio. Un cálculo matemático decide definitivamente la cuestión, y la decisión es enteramente adversa a la hipótesis de Laplace. Aparte de detalles menores, el proceso imaginado por Laplace explica el nacimiento de soles a partir de nebulosas; no puede explicar el nacimiento de los planetas a partir de los soles.
Teorías del segundo cuerpo. Laplace imaginó que su sol estaba solo en el espacio, incluso sus vecinos más cercanos estaban demasiado lejos para influir en él de alguna manera. Era la suposición natural a hacer; ya hemos comentado cuán extremadamente raro debe ser un evento para que dos estrellas se acerquen lo suficiente como para influirse mutuamente. Sin embargo, ningún modo posible de evolución de una estrella que permanece sola en el espacio parece capaz de explicar el [ p. 235 ] origen del sistema solar. Ya en 1750, Buffon había sugerido que el sistema solar podría haber sido producido a través de la interrupción del sol por otro cuerpo, al que describió como un «cometa». Al proponer su Hipótesis Nebular, Laplace mencionó la idea de Buffon, pero la descartó un tanto bruscamente sobre la base de que parecía incapaz de explicar las órbitas casi circulares de los planetas, una objeción mal fundada, como pronto veremos. Sin embargo, cuando encontramos que una sola estrella no puede por sí sola dar a luz a un sistema solar, se vuelve natural investigar qué sucede en las raras ocasiones en que la evolución de una estrella se dirige a lo largo de otros caminos por el acercamiento de una segunda estrella.
En 1880, Bickerton de Nueva Zelanda, reviviendo la idea de Buffon, supuso que el sistema solar se había formado por la colisión del sol con otra estrella. Imaginó los escombros de la colisión para formar un tercer cuerpo nebuloso, condensaciones en las que se formaron los planetas. Mostró cómo la resistencia que encontrarían los planetas al moverse a través de la nebulosa circundante haría que sus órbitas se hicieran gradualmente más circulares, y así explicar sus formas casi circulares actuales. Diez años antes, el escritor inglés R. A. Proctor había adelantado ideas similares, aunque con menos precisión. En 1905, los profesores Chamberlin y Moulton de Chicago propusieron una modificación de las mismas ideas, bajo el nombre de «hipótesis planetesimal». Descartando la idea de colisión material, supusieron que una estrella que pasaba ejercía una poderosa fuerza de marea sobre el sol, con el resultado de que las prominencias solares ordinarias alcanzaban temporalmente una violencia extraordinaria; se suponía que la materia expulsada se elevaba a alturas inusuales y se condensaba en pequeños cuerpos sólidos, los «planetesimales», a partir de la agregación de [ p. 236 ] la que finalmente se formaron los planetas. Estas diversas teorías eran todas puramente especulativas. Han mostrado muy poca capacidad para sobrevivir a la dura prueba del análisis matemático o para explicar las características más sobresalientes del sistema solar; ninguno de ellas, por ejemplo, explica por qué los planetas más grandes del sistema solar están acompañados por familias de satélites.
Tres años antes de que Chamberlin y Moulton presentaran su teoría planetesimal, yo había especulado sobre la posibilidad de que las fuerzas de las mareas rompieran una estrella y generaran un sistema solar. En 1916, investigué matemáticamente lo que sucedería realmente cuando una estrella provocara violentas fuerzas de marea sobre otra. Los resultados que obtuve me parecieron demoler la teoría planetesimal de Chamberlin y Moulton, y me llevaron a proponer la actual «Teoría de las mareas», que creo que una gran proporción de astrónomos ahora aceptan como el origen más probable de la sistema solar; por supuesto, no puede pretender finalidad o certeza.
Teoría de las mareas. Cuando dos estrellas u otros cuerpos pasan cerca uno del otro sin colisionar, el efecto primario debe ser que cada uno levanta mareas en el otro. Cuanto más se acercan, más altas son las mareas en general, aunque algo debe depender también de la velocidad con la que los cuerpos se cruzan, porque ésta determina el tiempo durante el cual se influyen unos a otros.
Es probable que los dos brazos espirales que dan su nombre y apariencia característica a las nebulosas espirales deban su origen a una acción de marea algo similar. Las condiciones aquí son diferentes en el sentido de que la rotación de las nebulosas en cualquier caso hace que emitan materia en sus planos ecuatoriales, por lo que incluso las pequeñas fuerzas de marea deberían hacer que esta materia se concentre [< small>p. 237] en dos brazos simétricos. En condiciones estelares, es necesario acercarse mucho más para extraer materia de la estrella, y entonces lo más probable es que haya dos brazos desiguales y diferentes, o posiblemente solo un brazo.
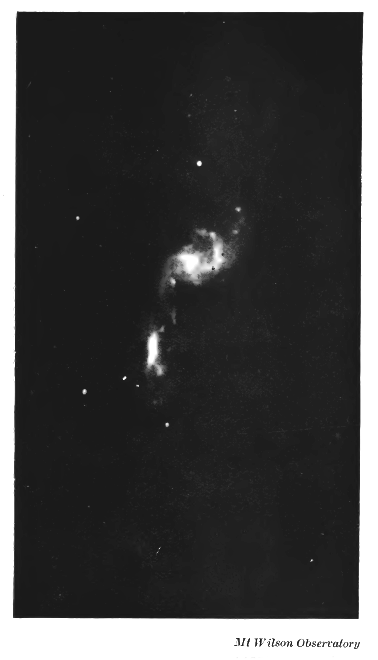
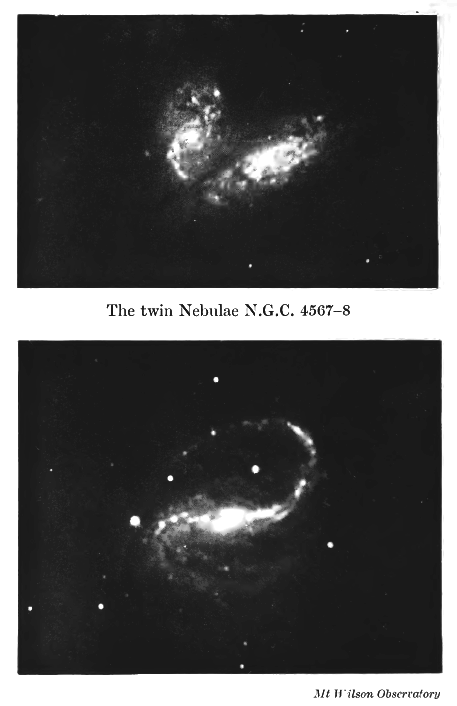
Si el acercamiento es realmente muy cercano, las mareas pueden asumir un aspecto enteramente diferente de las débiles mareas que el sol y la luna levantan en nuestros océanos; pueden tomar las formas exageradas de altas montañas de materia moviéndose sobre la superficie de la estrella. Un acercamiento aún más cercano puede transformar estas montañas en largos brazos de gas extraídos del cuerpo de la estrella. Si, como suele ser el caso, las dos estrellas tienen pesos diferentes, la menor sufrirá, en general, más perturbaciones que la mayor.
El nacimiento de los planetas. El largo brazo o filamento de materia extraído de una estrella por la acción de las mareas es al principio continuo en su estructura, pero el análisis muestra que proporciona un sujeto adecuado para la operación de lo que hemos llamado «Inestabilidad Gravitacional». En este largo brazo de gas comienzan a formarse condensaciones, de la forma ya descrita. Como antes, las condensaciones más pequeñas se disipan, mientras que las más grandes aumentan de intensidad hasta que finalmente el filamento se rompe en varias masas separadas: de la estrella más pequeña han nacido planetas. Los pares de nebulosas que se muestran en la Lámina XXII y la mitad superior de la Lámina XXIII muy probablemente se encuentran bajo la influencia de las mareas, y pueden servir para sugerir la naturaleza general del proceso que ahora estamos considerando.
Cuando los planetas recién nacidos comienzan a moverse como [ p. 238 ] cuerpos separados e independientes, actúan sobre ellos las fuerzas gravitatorias de ambas estrellas, por lo que describen órbitas muy complicadas. Gradualmente, la estrella más grande retrocede hasta que su efecto gravitatorio se vuelve insignificante, y los planetas se quedan describiendo órbitas alrededor de la estrella más pequeña. Si los planetas se movieran en un campo claro de espacio vacío, estas órbitas serían elipses exactas. Pero el gran cataclismo que acaba de ocurrir debe haber dejado atrás todo tipo de escombros. Los cometas, meteoros y otros cuerpos menores que aún sobreviven en el sistema solar pueden representar una pequeña parte de él, pero probablemente la mayor parte quedó en forma de polvo o gas. de modo que los planetas recién nacidos tuvieron que abrirse paso al principio a través de un medio que ofrecía cierta resistencia a sus movimientos. En estas circunstancias, sus órbitas no serían elipses estrictas. Se puede probar que una resistencia del tipo que acabamos de describir cambiaría la forma de las órbitas, y que con el transcurso del tiempo se volverían más circulares, convirtiéndose finalmente en absolutamente circulares si el medio durara lo suficiente.
Sin embargo, los restos de gas y polvo serían barridos continuamente por los planetas y desaparecerían por completo con el tiempo, probablemente dejando las órbitas planetarias algo por debajo de los círculos absolutos. Suponiendo que todo esto haya sucedido en el sistema solar, muy poco de los escombros originales puede quedar ahora, siendo sus últimos vestigios probablemente representados por las partículas de polvo que son responsables de la luz zodiacal. Sin embargo, el medio resistente parece haber existido durante el tiempo suficiente para hacer que las órbitas, tanto de los planetas como de sus satélites, fueran casi circulares en su mayor parte.
Los casos excepcionales son tan significativos como los [ p. 239 ] casos de conformidad. Todavía existen órbitas comparativamente alargadas en aquellas regiones en las que deberíamos esperar que el medio de resistencia primitivo se hubiera dispersado más escasamente en el espacio, es decir, en los confines más externos del sistema solar y de los diversos sistemas de satélites. Plutón, el planeta más exterior de todos, tiene una órbita más alargada que cualquier otro planeta. Nuevamente, en los sistemas de Júpiter y Saturno, los satélites con las órbitas más alargadas son los que están más alejados de sus primarias. Además de esto, se puede discernir una tendencia general a que las órbitas alargadas se asocien con pesos pequeños, tanto en los planetas como en sus satélites. Mercurio, con un peso de sólo una veinticinco parte del de la tierra, tiene una órbita bastante alargada, como también en menor grado la tiene Marte con una novena parte del peso de la tierra. Jeffreys ha sugerido una explicación de esto. Los planetas masivos como Júpiter y Saturno deben haber acumulado una gran masa del medio resistente a su alrededor y lo llevaron a través del espacio con ellos como una envoltura de gran alcance. Los planetas masivos verían frenado su movimiento por la interacción de toda esta gran envoltura con el resto del medio, y así alcanzarían órbitas circulares más rápidamente que los planetas más livianos que habían acumulado envolturas de dimensiones mucho más pequeñas. Y lo mismo, con las modificaciones oportunas, ocurre con los sistemas satelitales.
Jeffreys ha calculado la velocidad a la que las órbitas planetarias cambiarían de forma bajo la acción de este medio resistente. Los datos del problema son necesariamente inciertos, y esta incertidumbre naturalmente afecta sus conclusiones, pero su estudio ha producido una valiosa confirmación de otras estimaciones del tiempo transcurrido desde que nacieron los planetas.
[ p. 240 ] A continuación podemos centrar nuestra atención en los cambios físicos que durante todo este tiempo deben estar afectando a los diversos planetas. Es probable que el largo filamento de materia extraído del sol haya sido más rico en materia en sus partes medias, ya que estas partes se extrajeron cuando la segunda estrella estaba más cerca y su atracción gravitatoria era más fuerte. Al menos esquemáticamente, podemos pensar que este filamento tiene la forma de un cigarro: grueso cerca del medio, delgado en los extremos, de modo que cuando comienzan a formarse condensaciones, es probable que los que están cerca del medio sean más ricos en materia que los de los extremos. Esto probablemente explica por qué los dos planetas más masivos, Júpiter y Saturno, ocupan las posiciones intermedias en la secuencia de planetas.
La Fig. 14 muestra los planetas dispuestos en el orden de sus distancias al sol, con sus tamaños dibujados aproximadamente a escala. Los miles de asteroides cuyas órbitas ahora llenan el espacio entre las órbitas de Marte y Júpiter se representan como un solo planeta, suponiéndose generalmente que estos asteroides se formaron por la ruptura de lo que originalmente era un solo plano de una manera que veremos más adelante brevemente.
Si rodeamos los planetas con un contorno continuo, como en el diagrama, podemos reconstruir en la imaginación [ p. 241 ] el filamento en forma de cigarro a partir del cual se produjeron, y vemos de inmediato cómo se produjeron los planetas más grandes donde la materia era más abundante.
La teoría de las mareas que predice todas estas características se había propuesto, y sus consecuencias se habían resuelto, muchos años antes de que se descubriera el nuevo planeta Plutón. Por lo tanto, se puede encontrar un apoyo valioso para la teoría en la circunstancia de que Plutón se comporta en todos los sentidos de acuerdo con los requisitos de la teoría de las mareas.
El nacimiento de los satélites. Ya hemos notado cómo la gran disparidad de peso entre el sol y los planetas distingue la formación sol-planeta de la de la estrella binaria normal, y así sugiere orígenes completamente diferentes para las dos formaciones. Exactamente la misma disparidad se repite en los sistemas planeta-satélite. Así como el sol padre es enormemente más masivo que sus hijos los planetas, estos a su vez son mucho más masivos que sus hijos satélites. El sol tiene 1047 veces el peso de su planeta más masivo y muchos millones de veces el peso del más pequeño. En el sistema de Saturno las cifras correspondientes son 4150 y alrededor de 16.000.000. La aproximación más cercana a la igualdad de pesos la proporciona el sistema tierra-luna, teniendo la tierra sólo 81 veces el peso de la luna. Y, como el sistema planetario del sol, los sistemas de satélites de Saturno y, en menor grado, de Júpiter muestran una tendencia general a que los pesos de los diversos satélites aumenten hasta un máximo a medida que nos alejamos del planeta, y luego a disminuir de nuevo. Esto nuevamente sugiere la formación de un filamento en forma de cigarro con la mayor cantidad de materia cerca del medio. Junto con la repetición de la gran disparidad de pesos entre primarios y secundarios, esto indica de manera muy contundente que [ p. 242 ] los satélites de los planetas deben haber nacido por el mismo tipo de proceso que previamente resultó en el nacimiento de sus padres.
Podemos imaginar el proceso de forma general. Inmediatamente después de su nacimiento, los planetas deben comenzar a enfriarse. Los planetas más grandes, Júpiter y Saturno, naturalmente se enfrían más lentamente y los más pequeños más rápidamente. Estos últimos pueden perder calor con tanta rapidez que se licuan, y tal vez incluso se solidifican, casi inmediatamente después de su nacimiento. Mientras estos eventos están en progreso, los planetas siguen siguiendo órbitas un tanto erráticas, en las que pueden pasar tan cerca del sol que se produce una segunda serie de interrupciones de las mareas. En estos, el sol mismo juega el papel originalmente jugado por la estrella que pasa desde el espacio, y los planetas juegan el papel originalmente jugado por el sol. El sol puede ahora arrancar largos filamentos de materia de la superficie de los planetas, y estos, formando condensaciones, pueden dar nacimiento a otra generación de cuerpos astronómicos, los satélites de los planetas. De alguna manera, la teoría de las mareas imagina que los satélites planetarios han llegado a existir.
La investigación matemática muestra que cuanto más líquido era un planeta al nacer, menos probable sería que el sol aún gaseoso lo rompiera. Sin embargo, si ocurriera tal ruptura, los pesos del primario y los satélites serían casi iguales que si el planeta hubiera sido más gaseoso. Por lo tanto, al pasar de planetas totalmente gaseosos a planetas que se licuaron en su nacimiento o inmediatamente después, deberíamos esperar encontrar planetas con un gran número de satélites relativamente pequeños, y luego, después de pasar por los casos límite de planetas con pequeño número de satélites relativamente grandes, deberíamos esperar encontrar planetas que no tengan ningún satélite.
[ p. 243 ] Ya hemos visto que los grandes planetas centrales, Júpiter y Saturno, deberían haber permanecido gaseosos durante más tiempo y los planetas más pequeños haberse licuado antes; ahora vemos que esta predicción de la teoría describe exactamente lo que realmente se encuentra en el sistema solar. Partiendo de Júpiter y Saturno, cada uno con nueve satélites relativamente pequeños, pasamos a Marte con solo dos satélites y llegamos a la Tierra con su satélite relativamente grande, seguido por Venus y Mercurio, que no tienen ningún satélite. Procediendo en la otra dirección, dejamos a Júpiter y Saturno cada uno con sus nueve pequeños satélites, para descubrir a Urano con cuatro satélites pequeños y Neptuno con un satélite comparativamente grande. El número colocado debajo de cada planeta en la fig. 14 da el número de sus satélites. Cuando los números se exhiben de esta manera, la ley y el orden en la disposición de los sistemas de satélite se vuelven muy evidentes, y se ve que esta disposición está exactamente de acuerdo con la predicción de la teoría de las mareas. El arreglo en forma de cigarro se aplica no solo a los tamaños de los planetas, sino también, como debe ser, al número de sus satélites.
La Tierra y Neptuno, con un solo satélite cada uno, y esos comparativamente grandes, forman las líneas obvias de demarcación entre los planetas que originalmente eran líquidos y los que originalmente eran gaseosos. Esto nos lleva a conjeturar que Mercurio, Venus y Plutón debieron volverse líquidos o sólidos inmediatamente después del nacimiento, que la Tierra y Neptuno eran en parte líquidos y en parte gaseosos, y que Marte, Júpiter, Saturno y Urano nacieron gaseosos y permanecieron gaseosos al menos hasta después del nacimiento de sus familias de satélites.
Tal vez podamos encontrar más pruebas confirmatorias [ p. 244 ] de la teoría de las mareas en la circunstancia de que los pesos de Marte y Urano son anormalmente pequeños para sus posiciones en la secuencia de planetas. Si, como hemos supuesto, los planetas nacieron todos de un filamento continuo de materia, el peso de Marte al nacer habría sido con toda probabilidad intermedio entre los de la Tierra y Júpiter, y el peso de Urano intermedio entre los de Neptuno y Saturno. Pero si, como ya se nos ha hecho suponer, los dos planetas anómalos Marte y Urano fueron los dos planetas más pequeños que nacieron en estado gaseoso, probablemente perderían más de su sustancia que los otros planetas a través de sus capas más externas de moléculas que se disipan en el espacio antes de que se hayan enfriado al estado líquido. Si se supone que Marte y Urano son meras reliquias de planetas que inicialmente eran mucho más masivos de lo que son ahora, las anomalías comienzan a desaparecer y las piezas del rompecabezas encajan de manera muy satisfactoria.
Planos orbitales. Toda masa giratoria, ya sea gaseosa, líquida o sólida, tiene un eje de rotación definido y, perpendicular a éste, un plano ecuatorial definido que divide simétricamente la masa en dos mitades exactamente iguales y similares. Cuando una masa se rompe por su propia rotación, el plano ecuatorial y la simetría aún persisten. Se pueden encontrar ilustraciones de esto en cualquier conjunto de fotografías de nebulosas en rotación, como, por ejemplo, las que se muestran en las Láminas XV y XVI. En algo más ordinario proporcionan un ejemplo las salpicaduras de barro arrojadas por una rueda de bicicleta que gira, que se mantienen todas en el plano en el que gira la rueda.
Si el plano ecuatorial del sol hubiera resultado ser un [ p. 245 ] plano de simetría para el sistema solar, de modo que todo el sistema estuviera dispuesto de manera similar con respecto a los dos lados de este plano, podría haber sido posible explicar el sistema como el resultado de una ruptura rotacional. Pero el plano ecuatorial del sol no es un plano de simetría. Los planetas no se mueven en él, la mayoría se mueven en un plano que forma un ángulo de 5 o 6 grados con él. En términos de nuestra humilde analogía, las salpicaduras de barro no están volando en el plano en el que gira la rueda de la bicicleta.
La hipótesis de que los planetas surgieron a través de una ruptura rotacional del sol falla por completo ante este hecho, pero la teoría de las mareas proporciona una explicación simple de inmediato. El sol sigue girando como lo hacía antes de que nacieran los planetas, por lo que conserva su plano ecuatorial original. El plano completamente diferente en el que los planetas están describiendo órbitas, o muy cerca del mismo, debe ser claramente el plano en el que la estrella pasajera extrajo originalmente el largo filamento de las mareas. Así, el plano en el que ahora se mueven los planetas exteriores debe registrar la posición del plano en el que las dos estrellas, el sol y la estrella errante, el segundo padre de la familia de hijos del sol, describieron órbitas una alrededor de la otra hace 2000 millones de años. Es la única pista que le queda a este último de su identidad, y, por supuesto, es demasiado leve para hacer posible la identificación después de este largo lapso de tiempo.
En resumen, hemos visto que el mecanismo normal por el cual se ha tallado la mayor parte del universo es el nacimiento de sucesivas generaciones de cuerpos astronómicos por acción de la «inestabilidad gravitatoria».
La genealogía normal funciona de la siguiente manera:
caos — nebulosas — estrellas — sistemas binarios — subsistemas.
[ p. 246 ] No todas las estrellas han pasado a las últimas dos generaciones; donde solo estaba presente una pequeña cantidad de rotación, una estrella bien podría vivir toda su vida sin más subdivisiones. Nuestro sol habría proporcionado un ejemplo de esto si no hubiera sido por el raro accidente del acercamiento cercano de una segunda estrella. De la interacción de estos surgieron otras dos generaciones, siempre por el mecanismo de la inestabilidad gravitatoria. Para nuestro sistema solar, como para cualquier otro sistema similar que pueda haber en el cielo, la genealogía es la siguiente:
caos — nebulosa — sol — planetas — satélites.
Ambos tipos de genealogía muestran cinco generaciones, cada una nacida de su padre por la acción de la inestabilidad gravitatoria, y entre ellas las dos genealogías incluyen prácticamente todos los objetos astronómicos de gran tamaño que conocemos. Entonces, es justo decir que la «inestabilidad gravitatoria» parece ser la agencia principalmente responsable de la arquitectura principal del universo.
Límite de Roche. El reinado de la inestabilidad gravitatoria debe terminar con el nacimiento de los satélites planetarios, ya que cuerpos gaseosos de menor peso que estos no podrían mantenerse unidos. Incluso en las circunstancias más favorables, sus débiles fuerzas gravitatorias serían incapaces de impedir que sus moléculas más exteriores escaparan, de modo que toda la masa se dispersaría rápidamente por el espacio. Sin embargo, la astronomía proporciona muchos ejemplos de cuerpos más pequeños; ya hemos mencionado los asteroides, meteoros o estrellas fugaces, y las partículas de los anillos de Saturno. Como todos estos son demasiado pequeños para haber nacido en estado gaseoso, debemos suponer que son fragmentos fragmentados de masas más grandes. Esto concuerda con la circunstancia de que estos pequeños [ p. 247 ] cuerpos por regla general no ocurren individualmente sino en enjambres.
Los asteroides ocurren como un solo enjambre. Si estos se encontraran dispersos por todo el sistema solar, su origen podría presentar un problema difícil. Tal como están las cosas, todo el enjambre puede explicarse simplemente como los fragmentos rotos de un planeta primitivo. Los anillos de Saturno nuevamente admiten una explicación natural como los fragmentos de una antigua luna rota de Saturno. Los cometas, que apenas hemos tenido ocasión de mencionar hasta ahora, son con toda probabilidad enjambres de cuerpos diminutos que se mantienen unidos lo suficiente por su atracción gravitatoria mutua para describir una órbita común en el espacio. En su aparición en 1909, se estimó que el cometa Halley reflejaba tanta luz solar como un solo cuerpo de 25 millas de diámetro. Sin embargo, su superficie aparente era 300.000 veces mayor que la de dicho cuerpo y era bastante transparente.
Las estrellas fugaces, o meteoros, también se encuentran en enjambres. Como veremos más adelante, el movimiento de muchos de estos enjambres permite identificarlos como cometas fragmentados. Así, los fragmentos rotos que componen un cometa son idénticos a los meteoros que vemos como estrellas fugaces cuando penetran en la atmósfera terrestre. Shapley ha estimado que la atmósfera terrestre debe atrapar miles de millones de estrellas fugaces todos los días, de las cuales, como máximo, solo una de cada cien es lo suficientemente brillante como para ser visible a simple vista. Generalmente se disuelven en vapor antes de alcanzar la superficie terrestre (ver p. 176); ocasionalmente uno [ p. 248 ] es tan grande que la atmósfera terrestre no logra disiparlo por completo, y lo que queda de él golpea la tierra como un cuerpo sólido: un meteorito. Cada estrella fugaz y meteorito puede considerarse como un cometa en miniatura, que consta de un solo fragmento. En ocasiones, un grupo completo de fragmentos, moviéndose en trayectorias paralelas a distancias pequeñas, pueden golpear la atmósfera terrestre y aparecer como una «bola de fuego». Hablando en términos generales, todos los pequeños alevines del sistema solar se mueven en enjambres, y pueden interpretarse naturalmente como fragmentos descompuestos de cuerpos más grandes.
Si los meteoritos son fragmentos rotos de cuerpos que nacieron del sol al mismo tiempo que los planetas, debieron solidificarse aproximadamente al mismo tiempo que la tierra, en una época que hemos situado hace unos 2000 millones de años. Pero si hubieran nacido de alguna otra estrella, el momento de su solidificación podría haber sido en cualquier lugar hasta hace millones de millones de años.
El profesor Paneth y dos colegas de Konigsberg han estimado recientemente las edades de varias piedras meteóricas mediante métodos similares a los empleados para fijar la edad de la Tierra (p. 154). Obtienen edades que van desde unos pocos millones de años hasta 2900 millones de años, pero no hay nada más allá de esta última cifra. Ni una sola piedra sugiere una edad que se acerque a millones de millones de años. Esto proporciona una evidencia muy sólida de que estas piedras fueron producto del mismo cataclismo que produjo la tierra y, de paso, proporciona una valiosa confirmación de nuestra estimación previa de la edad de la tierra.
Podemos ver fácilmente cómo los cuerpos más grandes pueden dividirse en enjambres de meteoros. Hemos supuesto que el sol se ha roto, al menos hasta el punto de expulsar [ p. 249 ] una familia de planetas, por la fuerza de marea de una estrella que pasa. ¿Qué hubiera pasado si la estrella pasajera no hubiera pasado, sino que hubiera tenido que quedarse? Mientras permaneciera a cierta distancia del sol, sus fuerzas de marea estaban desgarrando al sol. Podemos imaginar cómo una visita más prolongada habría resultado en una mayor agitación en el sol y el nacimiento de una familia más grande de planetas. Finalmente, una visita de duración ilimitada habría hecho añicos el sol.
En 1850, Roche realizó una investigación matemática de este proceso de ruptura de las mareas. Su discusión trató solo con cuerpos sólidos o líquidos, pero el mecanismo subyacente es el mismo ya sea que los cuerpos sean sólidos, líquidos o gaseosos. Hemos visto que el más pequeño de los dos cuerpos involucrados en un encuentro de mareas es el que más sufre. Roche se ocupó únicamente del caso en que un cuerpo era muy pequeño en comparación con el otro; en tal caso, el cuerpo pequeño estaba completamente roto, mientras que el más grande permanecía ileso. Roche imaginó el cuerpo pequeño para describir una órbita de tamaño gradualmente decreciente alrededor del cuerpo grande. Si los dos cuerpos tuvieran la misma densidad, calculó que el cuerpo pequeño se rompería tan pronto como el radio de su órbita descendiera a 2,45 veces el radio del cuerpo grande. Si los cuerpos son de diferente densidad, el asunto es un poco más complicado. Debemos imaginar que el cuerpo más grande se expande o se contrae hasta que tenga la misma densidad promedio que el cuerpo más pequeño; la distancia crítica es entonces 2,45 radios del cuerpo más grande en su estado imaginario expandido o contraído.
Esta distancia se conoce generalmente como límite de Roche. Un satélite puede describir con seguridad una órbita circular alrededor de su primaria siempre que esta órbita se encuentre más allá del límite de Roche, pero se rompe en fragmentos tan pronto como [ p. 250 ] traspasa dentro del límite. Las siguientes cifras confirman el análisis matemático de Roche:
| Radio | Valor |
|---|---|
| Radio del anillo más exterior de Saturno | 2,30 radios de Saturno |
| Límite de Roche | 2,45 radios de primaria |
| Radio de órbita del satélite más interno de Saturno | 3,11 radios de Saturno |
| Radio de órbita del satélite más interno de Júpiter | 2,54 radios de Júpiter |
| Radio de órbita del satélite más interno de Marte | 2,79 radios de Marte |
Al mismo tiempo, sugieren con mucha fuerza que los anillos de Saturno son los fragmentos rotos de un antiguo satélite que se aventuró en la zona de peligro marcada por el límite de Roche. Hemos visto cómo nuestra propia luna está destinada en el tiempo a contraer su órbita, hasta que finalmente sea arrastrada dentro del límite de Roche que rodea la tierra y se rompa en fragmentos. Después de esto la tierra no tendrá luna, sino que estará rodeada de anillos como Saturno.
Hablamos de los anillos de Saturno en plural, porque dos espacios circulares distintos provocan la apariencia de tres anillos separados. Hay una tendencia a saltar a la inferencia apresurada de que los anillos son los restos destrozados de tres satélites distintos, pero no es así. Goldsbrough ha mostrado cómo ciertas órbitas alrededor de Saturno se vuelven inestables por los movimientos de los satélites más grandes de Saturno, de modo que ninguna partícula podría permanecer permanentemente en tal órbita. Ha calculado posiciones para estas órbitas inestables, y se encuentra que concuerdan exactamente con las posiciones de las divisiones observadas entre los anillos. Así, los anillos de Saturno fueron producidos con toda probabilidad por la rotura de un solo satélite. El anillo de pequeños satélites que nuestra luna finalmente formará alrededor de la tierra no tendrá divisiones, porque la tierra no tiene otras lunas que hagan inestables ciertas órbitas.

[ p. 251 ] La idea fundamental de Roche puede extenderse en muchas direcciones y admite diversas aplicaciones. Debe haber, por ejemplo, una zona de peligro, delimitada por un límite de Roche, que rodee al sol. La distancia de esta zona de peligro al sol depende de la densidad del cuerpo para el que es peligrosa (p. 249). Para un cuerpo que tenga la baja densidad de un cometa, la distancia será realmente muy grande. Cualesquiera que sean las distancias de sus zonas de peligro, los cometas deben pasar ocasionalmente a través de ellas y romperse al hacerlo. Se observó que dos cometas, el cometa de Biela (1846) y el cometa de Taylor (1916), se partieron en dos mientras estaban aproximadamente a la distancia de la tierra del sol, y en 1882 se vio que un cometa se dividía en cuatro partes. El cometa Biela regresó a su debido tiempo (1852) en forma de dos cometas distintos a un millón y medio de millas de distancia, desde entonces no se ha vuelto a ver ninguna parte del cometa original. La órbita de este cometa era idéntica a la de los meteoros Andrómedidas, que hacen un despliegue de estrellas fugaces en la atmósfera terrestre los 27 de noviembre favorables, por lo que es probable que estas estrellas fugaces sean los restos rotos del cometa Biela. Otros enjambres conspicuos de estrellas fugaces también se mueven en la pista de los cometas: las Leónidas, que solían hacer un espectáculo magnífico cada 33 años, se mueven en la pista del cometa 1866 I, las Perseidas en la pista de otro cometa (1862 II), y las Acuáridas en la trayectoria del famoso cometa Halley. En cada caso, no cabe duda de que las estrellas fugaces son fragmentos dispersos de los cometas.
De la misma manera un límite de Roche debe rodear al planeta Júpiter, del mismo modo los cometas y otros cuerpos pueden [ p. 252 ] romperse al entrar en la zona de peligro delimitada por este límite. El satélite más interno de Júpiter ya está peligrosamente cerca de él. Pero el mayor interés de esta zona de peligro en particular es que probablemente explica la existencia de los asteroides. En los primeros días del sistema solar, cuando las órbitas de los planetas eran menos circulares de lo que son ahora, un planeta primitivo entre Marte y Júpiter bien pudo haber descrito una órbita tan alargada como para llevarlo repetidamente dentro de la zona de peligro de Júpiter. Si es así, no necesitamos seguir buscando el origen de los asteroides. Es significativo que la órbita media de todos los asteroides coincida casi exactamente con la del planeta que la ley de Bode (p. 19) exigiría que existiera entre Marte y Júpiter.
¶ Notas
Esto es lo suficientemente cercano, pero no absolutamente exacto. El análisis matemático exacto muestra que el peso de la condensación mínima M está dado por
donde C, γ, ρ, κ son la velocidad molecular, la constante de gravitación, la densidad inicial y la relación de calores específicos, mientras que el peso del cual las moléculas que se mueven con velocidad C simplemente no logran escapar está dado por
Con $ \kappa = 1 \frac{2}{3}$ el peso mínimo de condensación es 9,7 veces el peso justo para retener las moléculas. ↩︎
ya se han mencionado las siguientes estimaciones:
Peso de la galaxia en términos de sol: 240,000,000,000
„ de la nebulosa M 31 en términos de sol: 3,500,000,000
„ „ NGC 4594 en términos de sol: 2,000,000,000 ↩︎Aunque los detalles no son importantes, el curso real de los acontecimientos sería que la Tierra comenzaría a describir una órbita elíptica en lugar de una circular alrededor del Sol, siendo la distancia promedio de la Tierra mayor que ahora. ↩︎