Autor: Sir James Jeans, M. A., D. Sc., Sc. D., LL. D., F. R. S.
[ p. 16 ]
Hemos visto cómo el hombre, después de habitar la tierra durante 300.000 años, en los últimos 300 años, la última milésima parte de su vida en la tierra, ha llegado a poseer un medio óptico para estudiar el universo exterior. En el presente capítulo trataremos de describir las impresiones que se ha formado con sus ojos recién despiertos. La descripción se organizará en un orden cronológico muy aproximado. Este es también un orden de poder telescópico creciente, o de ver nuevamente más y más lejos en el espacio, de modo que nuestro orden de disposición podría describirse igualmente como uno de distancia creciente respecto el sol. No intentaremos ningún tipo de registro continuo, sino que simplemente mencionaremos algunos hitos para mostrar a grandes rasgos el orden en que se ganó y consolidó el territorio en la exploración del universo por parte del hombre.
¶ El sistema solar
Convenientemente, podemos comenzar con el sistema solar, cuya estructura fue descifrada por Galileo y sus sucesores.
La familia de planetas del sol cae naturalmente en grupos distintos. Cerca del sol están los cuatro pequeños planetas, Mercurio, Venus, la Tierra y Marte. A distancias mucho mayores se encuentran los cuatro grandes planetas, Júpiter, Saturno, Urano y Neptuno. Más allá de todo esto está el recién descubierto planeta Plutón, el miembro más externo de nuestro sistema conocido hasta ahora.
Mercurio es el más cercano de todos al sol; luego viene Venus. Las órbitas de estos dos planetas se encuentran entre la [ p. 17 ] la órbita de la tierra y el sol. Vistos desde la tierra, estos planetas parecen describir círculos relativamente pequeños alrededor del sol, por lo que necesariamente deben aparecer cerca del sol en el cielo. Como consecuencia, solo se pueden ver temprano en la mañana, si sucede que salen justo antes del sol, o al atardecer si se ponen después del sol. Los antiguos no reconocieron del todo que los mismos planetas podían aparecer como estrellas matutinas y vespertinas, y les dieron diferentes nombres según figuraran como uno u otro. Como lucero del alba, Venus fue llamado Fósforo por los griegos y Lucifer por los romanos; como estrella vespertina ambos lo llamaron Héspero.
Después de la tierra, saliendo del sol hacia el espacio, viene Marte, completando el grupo de pequeños planetas. Marte, Venus y Mercurio son todos más pequeños que la Tierra en tamaño, aunque Venus lo es solo un poco.
Hay una gran brecha entre la órbita de Marte, el último de los pequeños planetas, y la de Júpiter, el primero de los grandes planetas. Esto no está vacío; está ocupado por las órbitas de miles de pequeños planetas conocidos como asteroides. Ninguno de estos se acerca en tamaño a la tierra; Ceres, el más grande, tiene solo 480 millas [772 km] de diámetro, y solo se conocen cuatro con diámetros de más de 100 millas [161 km]. Los planetas Mercurio, Venus y Marte se conocen desde la antigüedad remota, pero los asteroides entraron en la astronomía recién en el siglo XIX, siendo Ceres, el primero y el más grande, descubierto por Piazzi el 1 de enero de 1801.
Más allá de los asteroides vienen los cuatro grandes planetas Júpiter, Saturno, Urano y Neptuno, todos ellos mucho más grandes que la Tierra. Júpiter, el más grande, tiene, según Sampson, un diámetro de 88.640 millas [142.652 km], o [ p. 18 ] más de once veces el diámetro de la tierra; mil cuatrocientos cuerpos del tamaño de la Tierra podrían estar empaquetados dentro de Júpiter y dejar espacio de sobra. Saturno, que le sigue en orden, solo es superado por Júpiter en tamaño, con un diámetro de unas 70.000 millas [112.654 km]. Estos dos son, con mucho, los más grandes de los planetas.
Urano y Neptuno tienen cada uno unas cuatro veces el diámetro, es decir, unas sesenta y cuatro veces el volumen de la Tierra. El tamaño de Plutón aún no se conoce con precisión, pero difícilmente puede ser más grande que la Tierra y probablemente sea considerablemente más pequeño.
Júpiter y Saturno forman objetos tan conspicuos en el cielo que necesariamente se conocen desde los primeros tiempos, pero Urano y Neptuno son descubrimientos comparativamente recientes. Sir William Herschel descubrió a Urano de manera bastante accidental en 1781, mientras miraba a través de su telescopio sin otro motivo que la esperanza de encontrar algo interesante en el cielo. Por el contrario, Neptuno fue descubierto en 1846 como resultado de intrincados cálculos matemáticos, que muchos consideraron en ese momento como el mayor triunfo de la mente humana, al menos desde la época de Newton. Fue un triunfo de la juventud. El honor debe repartirse en partes aproximadamente iguales entre un inglés, John Couch Adams, que entonces solo tenía 27 años y luego fue profesor de astronomía en Cambridge, y un joven astrónomo francés, Urbain J. J. Leverrier, quien era solo ocho años mayor que él. Ambos atribuyeron ciertos caprichos en el movimiento observado de Urano a la atracción gravitacional de un planeta exterior, y ambos se pusieron a trabajar para calcular la órbita en la que este supuesto planeta exterior debe moverse para explicar estos caprichos.
[ p. 19 ] Adams terminó sus cálculos primero e informó a los observadores en Cambridge sobre la parte del cielo en la que debería estar el nuevo planeta. Como resultado, Neptuno fue observado dos veces, aunque sin ser identificado inmediatamente como el planeta buscado. Antes de que se estableciera esta identificación en Cambridge, Leverrier había terminado sus cálculos y comunicado sus resultados a Galle, un asistente en Berlín, quien pudo identificar el planeta de inmediato, ya que Berlín poseía mejores mapas estelares de la región del cielo en cuestión de los que eran accesibles en Cambridge.
Gradualmente se supo que la atracción gravitacional de Neptuno era inadecuada para explicar todos los caprichos de los movimientos de Urano, mientras que caprichos similares comenzaron a aparecer en el propio movimiento de Neptuno. Esto apuntaba a la existencia de otro planeta más, incluso más lejos que Neptuno. Tal como lo habían hecho Adams y Leverrier en la ocasión anterior, el Dr. Percival Lowell, del Observatorio Flagstaff, Arizona, calculó la órbita en la que el nuevo planeta conjeturado, el «Planeta X», debería moverse, pero solo recientemente (marzo de 1930), después de muchos años de cuidadosa búsqueda, los observadores de Flagstaff descubrieron el planeta Plutón, moviéndose casi exactamente en la órbita que Lowell había predicho quince años antes.
Ya en 1772, Bode había señalado una relación numérica simple que conectaba las distancias de los diversos planetas al sol. Esto se obtiene de la siguiente manera: Escriba primero la serie de números
0 1 2 4 8 16 32 64 128 256
en el que cada número después de los dos primeros es el doble del anterior. Multiplique cada uno por tres, obteniendo así
0 3 6 12 24 48 96 192 384 768
[ p. 20 ] y agregue cuatro a cada uno, dando
4 7 10 16 28 52 100 196 388 772
Estos números son muy aproximadamente proporcionales a las distancias reales de los planetas al sol, que son (tomando la distancia de la tierra como 10):
| 3.9 | 7.2 | 10.0 | 15.2 | 26,5 | 52,0 | 95,4 | 191.9 | 300.7 | 400 |
|---|---|---|---|---|---|---|---|---|---|
| Mercurio | Venus | Tierra | Marte | Asteroides | Júpiter | Saturno | Urano | Neptuno | Plutón |
La ley fue enunciada antes de que se descubrieran Urano y los asteroides, por lo que es un tanto notable que éstos encajen tan bien en los lugares predichos. Por otro lado, la ley falla por completo para Neptuno y el recién descubierto Plutón, por lo que parece más que probable que se trate de una mera coincidencia sin una explicación racional subyacente.
Los planetas más exteriores están a enormes distancias del sol. Un habitante de Plutón, si tal existiera, recibiría sólo una dieciséis centésima parte de la luz y el calor del sol que recibe un habitante de la tierra. Se puede calcular que si la superficie de Plutón fuera calentada solo por el calor del sol, estaría a una temperatura muy baja, en algún lugar cercano a los -230° centígrados, o más de 400 grados de escarcha en la escala Fahrenheit.
Un telescopio recoge calor además de luz. No solo es tremendo el poder de acumulación de calor de un gran telescopio, sino que se han diseñado instrumentos extremadamente sensibles para medir este calor. Se dice que el telescopio de 100 pulgadas en Mount Wilson es capaz de detectar el calor recibido de una sola vela en las orillas del Mississippi, a 2000 millas [3.219 km] de distancia. Esta excelente [ p. 21 ] sensibilidad ha hecho posible medir las cantidades infinitesimales de calor recibidas de estrellas y planetas individuales, y así estimar las temperaturas de sus superficies. Mediciones recientes indican que la superficie de Júpiter está a una temperatura de alrededor de -150° centígrados, que es casi la temperatura a la que se mantendría sólo con el calor del sol. Por otro lado, medidas similares asignan temperaturas de -150° y -170° respectivamente a Saturno y Urano, las cuales son bastante más altas de lo que se esperaría si estos planetas no tuvieran una fuente de calor más allá de la radiación del sol. Pero parece claro que cualquier fuente de calor interno debe ser bastante pequeña y que todos los planetas principales son realmente muy fríos. No puede haber mares ni ríos en su superficie, ya que toda agua debe congelarse en hielo, ni puede haber lluvia o vapor de agua en sus atmósferas. Se ha sugerido que las nubes que oscurecen nuestra visión de la superficie de Júpiter pueden ser partículas condensadas de dióxido de carbono, o algún otro gas que hierve a temperaturas muy por debajo del punto de congelación del agua.
Las condiciones físicas de los planetas más pequeños son mucho más parecidas a aquellas con las que estamos familiarizados en la Tierra. Debido a su mayor distancia del sol, Marte es algo, pero no enormemente, más frío que la tierra. Su día de 24 horas 37 minutos es solo un poco más largo que el nuestro, por lo que su superficie debe experimentar alternancias de calor durante el día y frío por la noche similares a las que encontramos en la tierra. En las regiones ecuatoriales la temperatura sube muy por encima del punto de congelación al mediodía, alcanzando ocasionalmente los 50° Fahrenheit [10° Celsius] o incluso más. Pero incluso aquí cae por debajo del punto de congelación algún tiempo antes de la puesta del sol, y desde entonces hasta [ p. 22 ] al día siguiente, el clima debe ser muy frío. Las regiones polares son, por supuesto, aún más frías, la temperatura de la capa de nieve que cubre los polos es de unos -70° centígrados o -94° Fahrenheit, ¡126 grados de escarcha!
Venus, al estar más cerca del sol, debe tener una temperatura promedio más alta que la tierra. Pero como cada uno de sus días y noches son varios días de nuestro tiempo terrestre, la diferencia entre las temperaturas del día y de la noche debe ser mucho mayor que entre nosotros, por lo que su superficie debe experimentar grandes extremos de calor de día y de frío de noche. La temperatura nocturna parece ser bastante uniforme e igual a aproximadamente -25° centígrados o -13° Fahrenheit. En cualquier punto de la superficie del planeta, las semanas de esta temperatura nocturna extremadamente fría deben alternar con semanas de una temperatura diurna abrasadora.
Mercurio está tan cerca del sol que su temperatura promedio es necesariamente mucho más alta que la de la tierra. Refleja solo una pequeña fracción, alrededor de un catorceavo, de la luz y el calor que recibe del sol. Todo el resto se destina a calentar su superficie. Varias consideraciones hacen probable que el planeta siempre dé la misma cara al sol, al igual que la luna siempre da la misma cara a la tierra. Si es así, la mitad no calentada de su superficie debe estar intensamente fría y la mitad calentada intensamente caliente. Se puede calcular que en este caso el hemisferio calentado debe tener una temperatura de unos 357° centígrados; sin embargo, si el planeta estuviera en rotación bastante rápida, toda su superficie tendría una temperatura de sólo unos 170° centígrados. Muy recientemente, Pettit y Nicholson midieron la cantidad de calor recibido en la Tierra desde el hemisferio calentado y descubrieron que su temperatura debe ser de unos 350° centígrados o 662° Fahrenheit, por lo que [p. 23] confirmando que el planeta siempre da la misma cara al sol. Su hemisferio cálido está a una temperatura que funde el plomo; el otro hemisferio, eternamente oscuro y sin calor, es probablemente más frío que cualquier cosa que podamos imaginar.

El descubrimiento de Galileo de los cuatro satélites de Júpiter fue seguido en el tiempo por el descubrimiento de que todos los planetas tenían satélites, excepto los dos cuyas órbitas se encontraban dentro del de la Tierra. En 1655 Huyghens descubrió Titán, el mayor de los satélites de Saturno, y en 1684 Cassini había descubierto cuatro más. Luego, después del lapso de un siglo completo, Sir William Herschel descubrió dos satélites de Urano en 1787 y dos satélites más de Saturno en 1789. Discutiremos el sistema completo de satélites planetarios y también los cuerpos más pequeños del sistema solar: cometas, meteoros y estrellas fugaces, en un capítulo posterior, cuando tratemos la forma en que surgieron.
¶ El Sistema Galáctico
Nuestro próximo hito es el reconocimiento de las estrellas por los dos Herschel, Sir William Herschel, el padre (1738-1822) y Sir John Herschel, el hijo (1792-1871). Lo que Galileo había hecho por el sistema solar, los dos Herschels se propusieron hacerlo por la enorme familia de estrellas, el sistema «galáctico», delimitado por la Vía Láctea, del cual nuestro sol es miembro.
En una noche clara sin luna, la Vía Láctea se extiende, como un gran arco de luz tenue, de horizonte a horizonte. Se encuentra que es solo una parte de un círculo completo de luz, el círculo galáctico, que se extiende completamente alrededor de la tierra y divide el cielo en dos mitades iguales, formando una especie de «ecuador» celestial, con referencia al cual los astrónomos están acostumbrados [ p. 24 ] para medir la latitud y la longitud en el cielo. El telescopio de Galileo había demostrado que consiste en una multitud de estrellas débiles, cada una de ellas demasiado tenue para ser vistas individualmente sin ayuda telescópica (ver Lámina I). Y, como era de esperar, la interpretación adecuada de este gran cinturón de estrellas débiles ha demostrado ser fundamental para comprender la arquitectura del universo.
Si las estrellas estuvieran dispersas uniformemente a través del espacio infinito, al final llegaríamos a una estrella en cualquier dirección que miráramos, de modo que el cielo aparecería como un resplandor uniforme de luz intolerable. Es cierto que este no sería el caso si la luz se atenuara o se apagara después de viajar una cierta distancia, pero incluso entonces, el cielo parecería el mismo en todas las direcciones, porque no habría razón para que una parte del cielo estuviera más profusamente salpicada de estrellas que otra. Así, la existencia de la Vía Láctea muestra que el sistema de las estrellas no se extiende uniformemente hasta el infinito. Debe tener una estructura definida, y fue la arquitectura de esto lo que Sir William Herschel se dispuso a desentrañar. El trabajo que hizo para la mitad norte del cielo fue extendido posteriormente al hemisferio sur por su hijo, Sir John Herschel.
Comprenderemos mejor el método empleado por los Herschel si primero imaginamos que todas las estrellas del cielo son objetos intrínsecamente similares. Cada uno emitiría entonces la misma cantidad de luz, de modo que las estrellas más cercanas aparecerían brillantes y las estrellas más lejanas se debilitarían, simplemente como un efecto de la distancia. La forma en que el brillo aparente disminuye con la distancia es, por supuesto, bien conocida; la ley es la del «inverso del cuadrado de la distancia», lo que significa que el brillo aparente disminuye tan rápidamente como aumenta el cuadrado de su distancia; una estrella que está el doble de distante [ p. 25 ] que una segunda estrella similar aparece solo un cuarto de brillante, y así sucesivamente. Así, si todas las estrellas emitieran la misma cantidad de luz, podríamos estimar las distancias relativas de dos estrellas en el cielo a partir de sus brillos relativos. Cortando alambres de longitudes proporcionales a las distancias de varias estrellas, y apuntándolos en las direcciones de las estrellas a las que se refieren, podríamos formar un modelo de la disposición de las estrellas en el cielo. De hecho, deberíamos conocer toda la estructura del sistema de estrellas excepto su escala. Para representar las estrellas tenues de la Vía Láctea, se necesitaría una gran cantidad de cables muy largos. En el modelo, todos apuntarían hacia diferentes partes de la Vía Láctea, formando una estructura similar a una rueda plana.
El problema al que se enfrentó Sir William Herschel era más complicado porque sabía que las estrellas tenían un brillo intrínseco diferente, así como diferentes distancias, y ambos factores se combinaban para producir diferencias de brillo aparente. Una de las principales dificultades de la astronomía, tanto para los Herschel como para el astrónomo de hoy, es que estos dos factores deben desenredarse antes de llegar a conclusiones definitivas.
Herschel descubrió que el número de estrellas visibles en el campo de su telescopio variaba enormemente con diferentes direcciones en el espacio. Por supuesto, fue mayor cuando el telescopio apuntó a la Vía Láctea y cayó, constante y rápidamente, a medida que el telescopio se alejaba de la Vía Láctea. En términos generales, dos campos de telescopios que estaban a la misma distancia de la Vía Láctea contenían aproximadamente el mismo número de estrellas. En el lenguaje técnico de la astronomía, la riqueza del campo estelar dependía principalmente de la latitud galáctica, así como el clima terrestre depende principalmente de [ p. 26 ] la latitud geográfica, y no en gran medida en la longitud.
Se descubrió que los campos a diferentes distancias de la Vía Láctea diferían en calidad y en número de estrellas. Las estrellas más brillantes de todas aparecían casi por igual en todos los campos, la diferencia en los campos resultaba principalmente de las estrellas débiles, y particularmente de las estrellas más débiles de todas, volviéndose enormemente más abundantes a medida que se acercaba a la Vía Láctea.
Sir William Herschel interpretó acertadamente que esto demostraba que el sistema de estrellas que rodeaba al sol comenzaba a disminuir en las distancias alcanzadas por su telescopio, y que comenzaban a disminuir más rápidamente en las direcciones más alejadas de la Vía Láctea. Supuso que la forma general del sistema galáctico de estrellas era la de un bollo, una galleta o un reloj, estando las estrellas más densamente dispersas cerca del centro y más escasas en las regiones exteriores. El plano de la Vía Láctea, por supuesto, formaba el plano central de la estructura. El hecho de que la Vía Láctea divida el cielo en dos mitades casi exactamente iguales le sugirió que el sol debe estar muy cerca de este plano central, y esto lo confirman las recientes y muy refinadas investigaciones de Seares y van Rhijn, entre otros. Del hecho de que las partes del cielo que eran equidistantes de la Vía Láctea parecían igualmente brillantes, Herschel infirió que el sol no solo se encontraba en el plano central del sistema, sino que estaba muy cerca de su centro real. Este punto de vista ha prevalecido hasta hace poco tiempo, pero las investigaciones de Shapley y otros ahora muestran que es insostenible (ver p. 65 más adelante).
La Fig. 1 muestra una sección transversal del tipo general de estructura que Sir William Herschel asignó al sistema galáctico, aunque la distribución detallada de [ p. 27 ] estrellas que se muestran en el diagrama son las proporcionadas en una fecha muy posterior (1922) por Kapteyn. Es fácil ver cómo una estructura de este tipo explicaría la apariencia general del cielo. Las estrellas que parecen más brillantes de todas son, en general, las más cercanas; están tan cerca que no se produce un adelgazamiento apreciable de estrellas dentro de esta distancia. Por esta razón, las estrellas muy brillantes aparecen en cantidades aproximadamente iguales en todas las direcciones. Las estrellas que parecen muy débiles son en su mayoría muy distantes, tan distantes que entra en juego la gran profundidad del sistema en direcciones dentro o cerca del plano galáctico. En tales direcciones, las capas tras capas de estrellas, dispuestas casi infinitamente una tras otra, dan lugar a la aparente concentración de estrellas débiles que llamamos la Vía Láctea.
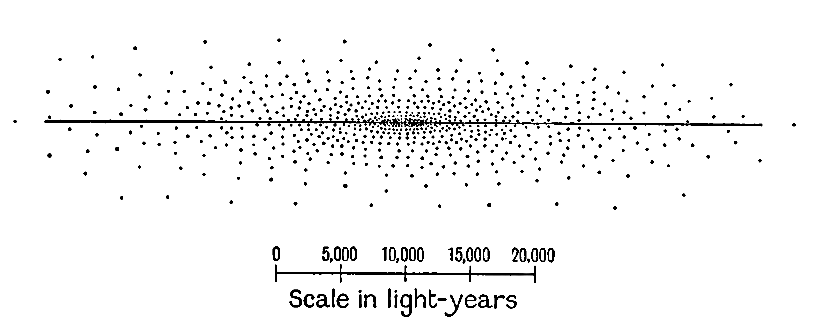
La aceptación final de la visión copernicana de la estructura del sistema solar se debió en gran medida al descubrimiento de Galileo del sistema similar de Júpiter, que estaba situado de tal modo en el espacio que un observador terrestre podía obtener una vista de pájaro de él como un todo. Nunca podemos obtener una vista de pájaro del sistema solar como un todo porque solo podemos verlo desde [ p. 28 ] dentro, por lo que la prueba óptica de que tales sistemas podrían existir, podría provenir solo del descubrimiento de otros sistemas similares, que podríamos ver desde el exterior.
Sir William Herschel creía que había confirmado su propia visión de la estructura del sistema galáctico de la misma manera, al descubrir sistemas similares, de los cuales podía obtener una vista de pájaro porque eran completamente ajenos a la galaxia. Habló de estos objetos como «universos islas» y creía que eran nubes de estrellas. Tenían una apariencia nebulosa, y aunque era imposible distinguir las estrellas separadas en ellos, creía que un suficiente poder telescópico lo haría posible, tal como le había permitido a Galileo ver las estrellas separadas en la Vía Láctea. Estos objetos, que describiremos casi inmediatamente, se conocen generalmente como «nebulosas extragalácticas» por su posición, aunque con frecuencia encontraremos conveniente utilizar el término más breve «grandes nebulosas», a las que su inmenso tamaño las hace merecedoras del nombre.
¶ Nebulosas
Un telescopio exhibe un planeta como un disco de tamaño apreciable, y un ocular que aumenta 60 veces hará que Júpiter parezca tan grande como la luna. Sin embargo, un ocular que aumenta 60 veces, o un número mayor de veces, nunca puede hacer que una estrella parezca tan grande como la luna. Ningún aumento dentro de nuestro control hace que una estrella aparezca como algo más que un mero punto de luz. Las estrellas son, por supuesto, enormemente más grandes que Júpiter, pero también están mucho más distantes, y es la distancia la que gana.
No obstante, el telescopio muestra una serie de objetos que parecen más grandes que meros puntos de luz. [ p. 29 ] Por lo general, tienen una apariencia tenue y nebulosa, por lo que han recibido el nombre general de «nebulosas». Una investigación detallada ha demostrado que estos se dividen en tres clases distintas.
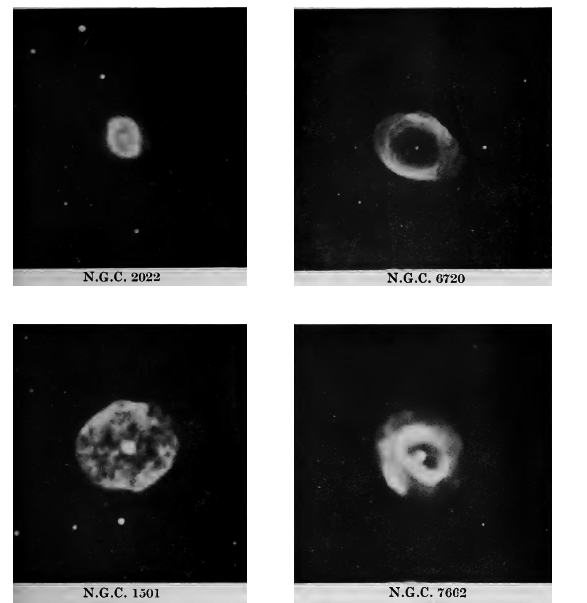

Nebulosas planetarias. La primera clase generalmente se describe como «Nebulosas planetarias». No hay nada de naturaleza planetaria en ellas más allá del hecho de que, como los planetas, se muestran como discos finitos en un telescopio. Solo se conocen unos pocos cientos de estos objetos, cuatro ejemplos típicos se ilustran en la Lámina II. Todos ellos se encuentran dentro del sistema galáctico. Discutiremos su estructura física más adelante (p. 321). Por el momento, baste decir que probablemente sean de naturaleza estelar que de algún modo se han rodeado de atmósferas luminosas de enorme extensión. Si es así, por supuesto refutan nuestra afirmación general de que ninguna estrella aparece nunca como algo más que un punto de luz en un telescopio; debemos hacer una excepción a favor de las nebulosas planetarias.
Nebulosas galácticas. La segunda clase se describe generalmente como «Nebulosas galácticas», y se muestran ejemplos en las Láminas III, VI (p. 37) y VII (p. 44). Estos son de forma completamente irregular. Su apariencia general es la de enormes volutas de gas resplandecientes que se extienden de estrella en estrella y, en efecto, esto es más o menos lo que son. Al igual que las nebulosas planetarias, se encuentran completamente dentro del sistema galáctico. Incluso una mirada superficial muestra que cada nebulosa irregular contiene varias estrellas enredadas con ella; un minucioso examen telescópico a menudo extiende las dimensiones de la nebulosa casi indefinidamente, de modo que podemos tener casi la totalidad de una constelación envuelta en una sola nebulosa.
Hay pocas dudas sobre la naturaleza física de estas nebulosas. El espacio entre las estrellas no está [ p. 30 ] completamente vacío de materia, pero está ocupado por una fina nube de gas de una tenuidad que generalmente es casi indescriptible. Aquí y allá esta nube puede ser más densa de lo habitual; aquí y allá puede iluminarse y volverse incandescente por la radiación de las estrellas en su interior. En otros lugares, puede ser completamente opaca a la luz, yaciendo como una cortina negra en el cielo. Las variaciones de densidad, opacidad y luminosidad combinadas producen todas las formas fantásticas y los variados grados de luz y sombra que vemos en las nebulosas galácticas.
Esta misma opacidad es la responsable de las manchas oscuras que se producen en la disposición general de las estrellas. Un ejemplo conspicuo ocurre en la parte de la Vía Láctea que se muestra en la Lámina I (p. 23). La mancha oscura, que al principio parece un agujero en el sistema de estrellas, se describe gráficamente como «El Saco de Carbón». Estas manchas negras en el cielo no pueden representar agujeros reales, porque es inconcebible que haya tantos túneles vacíos a través de las estrellas, todos apuntando exactamente hacia la tierra, de modo que nos vemos obligados a interpretarlos como velos de materia que oscurecen o apagan la luz de las estrellas detrás de ellos.
Nebulosas extragalácticas. La tercera clase de nebulosas es de una naturaleza completamente diferente. Sus miembros son en su mayor parte de forma definida y regular, y muestran varias otras características que las hacen fáciles de identificar. Solían llamarse «nebulosas blancas» por la calidad de la luz que emitían. Más tarde, el telescopio gigante de 6 pies [1,8 m] de Lord Rosse reveló que muchas de ellas tenían una estructura en espiral; estas fueron llamadas «nebulosas espirales». La más llamativa de todas las nebulosas espirales es la Gran Nebulosa M 31 en Andrómeda, que se muestra en la Lámina IV, que es apenas visible [ p. 31 ] a simple vista. Marius, al observarlo telescópicamente en 1612, la describió como «la luz de una vela vista a través de un cuerno». La Lámina V muestra un segundo ejemplo, probablemente de estructura muy similar, que se ve desde otro ángulo, de modo que aparece casi exactamente de canto.


Ahora está abundantemente probado que todas las nebulosas de este tipo se encuentran fuera del sistema galáctico, por lo que el término «nebulosas extragalácticas» las describe adecuadamente. Su tamaño es colosal. Cualquiera de las fotografías que se muestran en las Láminas IV y V tendrían que ser ampliadas al tamaño de toda Europa antes de que un cuerpo del tamaño de la Tierra se hiciera visible en ellas, incluso bajo un potente microscopio. Su forma general es similar a la que Sir William Herschel asignó al sistema galáctico, y fue esto lo que le llevó originalmente a considerarlos como «universos islas» similares al sistema galáctico. Veremos más adelante hasta qué punto su conjetura ha sido confirmada por investigaciones recientes.
¶ Las distancias de las estrellas
El año 1838 proporciona nuestro próximo hito; es el año en que se midió por primera vez la distancia de una estrella.
En el segundo siglo después de Cristo, Ptolomeo había argumentado que si la tierra se movía en el espacio, su posición relativa a las estrellas circundantes debía cambiar continuamente. Como la tierra giraba alrededor del sol, sus habitantes estarían en la posición de un niño en un columpio. Y así como el niño que se balancea ve los árboles más cercanos, las personas y las casas oscilando rítmicamente contra un fondo remoto de colinas y nubes distantes, así los habitantes de la tierra deberían ver las estrellas más cercanas cambiando continuamente su posición contra su [p. 32] fondo de estrellas más distantes. Sin embargo, noche tras noche las constelaciones seguían siendo las mismas, o eso argumentaba Ptolomeo; las mismas estrellas giraban eternamente en las mismas posiciones relativas alrededor del polo, y grupos visibles de estrellas como las siete estrellas de la Osa Mayor, las Pléyades o la constelación de Orión no mostraron signos de cambio. Por lo que podía decir el ojo humano sin ayuda, las estrellas podían ser manchas de pintura luminosa sobre un lienzo de fondo, con la tierra como eje inmóvil alrededor del cual giraba toda la estructura.
En oposición a esto, la teoría copernicana, por supuesto, requería que las estrellas más cercanas se vieran moverse contra el fondo de las estrellas más distantes, mientras la tierra realizaba su viaje anual alrededor del sol. Sin embargo, año tras año, e incluso siglo tras siglo, pasó sin que se detectara tal movimiento. La vieja afirmación ptolemaica de que la tierra formaba el centro fijo del universo casi podría haber recuperado su posición anterior, si no hubiera sido por las diversas líneas de evidencia que se habían comenzado a mostrar de que incluso las estrellas más cercanas estaban necesariamente muy distantes, tan distantes, de hecho, que su aparente falta de movimiento no debía causar sorpresa. El niño en un columpio no puede esperar tener evidencia óptica de su movimiento si el objeto más cercano que puede ver está a veinte millas [32 km] de distancia.
Muy pocas estrellas parecen más brillantes que Saturno en su punto más brillante; parecen tan brillantes como Altair, la undécima estrella más brillante del cielo. Sin embargo, Saturno brilla solo por la luz que refleja del sol, y su distancia del sol es tal que recibe solo una parte en 2500 millones de la luz total emitida por el sol. Y, como la superficie de Saturno solo refleja alrededor de dos quintas partes de la luz que recibe, se deduce que Saturno brilla con solo una 6000 millonésima parte de [ p. 33 ] la luz del sol. Si, como habían sostenido Kepler y otros, Altair era esencialmente similar al sol, probablemente tendría aproximadamente la misma potencia de candelas que el sol, y por lo tanto daría alrededor de 6000 millones de veces más luz que Saturno. El hecho de que Altair y Saturno parezcan igualmente brillantes en el cielo solo puede significar que Altair está 80.000 veces más lejos que Saturno[1]. Este argumento es esencialmente idéntico al que dio Newton en su Sistema del mundo para mostrar que incluso las estrellas más brillantes, como Altair, deben estar realmente muy distantes.
Y tal ha resultado ser el caso. Todos los esfuerzos para descubrir el movimiento oscilante aparente de las estrellas —«movimiento paraláctico», como se le llama técnicamente— que resulta del movimiento orbital de la Tierra fracasaron hasta 1838, cuando tres astrónomos, Bessel, Henderson y Struve, detectaron casi simultáneamente el movimiento paraláctico de las tres estrellas, 61 Cygni, α Centauri y α Lyrae respectivamente. La cantidad de su movimiento paraláctico hizo posible calcular las distancias de las estrellas, de modo que los habitantes de la tierra no sólo estaban en posesión de pruebas oculares definitivas de que giraban alrededor del sol, sino que con los efectos visibles de esta oscilación pudieron calcular las distancias de las estrellas más cercanas. Los valores calculados no eran precisos cuando se juzgaban según los estándares modernos, pero proporcionaron las primeras estimaciones definitivas de la escala sobre la que se construye el universo.
Hagamos una pausa por un minuto para considerar cómo se construye esta escala. El primer paso es seleccionar una línea de base conveniente de unas pocas millas de longitud en la superficie de la tierra, [ p. 34 ] y medirlo en términos de yardas o metros estándar. Partiendo de esta línea de base, un levantamiento geodésico mapea una franja larga y estrecha de la superficie terrestre, preferiblemente de norte a sur. La diferencia de latitud en los dos extremos se mide luego por métodos astronómicos, como por ejemplo notando la diferencia en la altitud de la estrella polar en los dos lugares. Como la longitud de la franja ya se conoce en millas, esto da inmediatamente las dimensiones de la tierra. Según Hayford (1909), el radio ecuatorial de la Tierra es de 6.378,388 kilómetros, o 3.963,34 millas, siendo su radio polar de 6.356,909 kilómetros o 3.949,99 millas.
El siguiente paso es determinar el tamaño del sistema solar en términos de la tierra. Cuando el sol es eclipsado por la luna, el momento en el que la luna comienza a cubrir el disco del sol es diferente para las diferentes estaciones en la superficie de la tierra, y las diferencias de tiempo observadas nos permiten medir la distancia de la luna en términos de distancias conocidas en la superficie de la tierra. De esta manera se encuentra que la distancia media de la luna es de 384.403 kilómetros o 238.857 millas. De la misma manera, el tránsito del planeta Venus a través del disco del sol brinda la oportunidad de determinar la escala del sistema solar en términos de las dimensiones de la tierra. El asteroide Eros ofrece aún mejores oportunidades. La Conferencia de París (1911) adoptó 149.450.000 kilómetros, o 92.870.000 millas, como el valor más probable para la distancia media de la tierra al sol. El próximo y último paso, que se completó en el año 1838, es el de usar el diámetro de la órbita terrestre como línea de base y determinar las distancias de las estrellas.
El primer paso, de la yarda o metro estándar a [ p. 35 ] la línea de base medida en la superficie de la tierra implica un aumento de varios miles de veces en longitud. El aumento involucrado en el siguiente paso, desde la línea de base hasta el diámetro de la tierra, es nuevamente uno entre miles. Y de nuevo el siguiente paso, del diámetro de la tierra al de la órbita de la tierra, implica un aumento de miles. Pero el último paso de todos, desde la órbita terrestre hasta las distancias estelares, implica un aumento de un millón de veces.
Mediciones recientes muestran que las estrellas más cercanas están a casi exactamente un millón de veces la distancia de los planetas más cercanos. En su máxima aproximación a la tierra, Venus está a 26 millones de millas [42 millones de km] de distancia, mientras que la estrella más cercana, Próxima Centauri, está a 25.000.000 millones de millas [40.233.600 millones de km] de distancia; esta última estrella es una tenue compañera de la conocida estrella brillante Centauri en el hemisferio sur. Las distancias de los planetas cuando están más cerca, y de las estrellas más cercanas, se muestran en la siguiente tabla:
| Planetas | Estrellas | |||
|---|---|---|---|---|
| Nombre | Distancia (millas; km) | Nombre | Distancia (millas; km) | Distancia (años luz) |
| Venus | 26.000.000; 42.000.000 | Proxima Centauri Centauri |
25.000.000; 40.233.600 millones | 4.27 4.31 |
| Marte | 35.000.000; 56.327.000 | Múnich 15040 | 36.000.000; 57.936.400 „ | 6.06 |
| Mercurio | 47,000,000; 75.639.200 | Lobo 359 Lalande 21185 Sirius |
47.000.000; 75.639.200 „ 49.000.000; 78.857.900 „ 51.000.000; 82.076.500 „ |
8.07 8.33 8.65 |
Como es casi imposible visualizar un millón, la mera afirmación de que las estrellas son un millón de veces más remotas que los planetas solo da una débil indicación de la inmensidad de la brecha que divide al sistema solar de sus vecinos más cercanos en el espacio. Tal vez la [ p. 36 ] la aparente fijeza de las estrellas da una impresión más vívida.
La tierra realiza su viaje anual alrededor del sol a una velocidad de aproximadamente 18½ millas por segundo [30 km/s], que es aproximadamente 1200 veces la velocidad de un tren expreso. El sol se mueve a través de las estrellas casi a la misma velocidad; para ser precisos, a unas 800 veces la velocidad de un tren expreso. Y, en términos generales, los planetas más cercanos y la mayoría de las estrellas se mueven con velocidades similares. No obtendremos una mala aproximación a la verdad si imaginamos que todos los cuerpos astronómicos se mueven con velocidades exactamente iguales, digamos, para fijar nuestros pensamientos, una velocidad igual a 1000 veces la velocidad de un tren expreso. Las distancias de los objetos astronómicos ahora son traicionadas por la velocidad con la que parecen moverse por el cielo: cuanto más lento es su movimiento aparente, mayores son sus distancias, y viceversa. Ahora bien, los planetas se mueven por el cielo con tanta rapidez que es bastante fácil detectar su movimiento de noche en noche e incluso de hora en hora; las estrellas se mueven tan lentamente que, excepto con ayuda telescópica, no se puede detectar ningún movimiento de generación en generación, o incluso de era en era. Incluso las constelaciones visibles del cielo, que en general están formadas por las estrellas más cercanas, han conservado su aspecto actual a lo largo de todos los tiempos históricos. El contraste entre los planetas que cambian de posición cada hora y las estrellas que no muestran ningún cambio apreciable en un siglo, da una vívida impresión de hasta qué punto las estrellas están más distantes que los planetas.
Es mucho más difícil visualizar las distancias reales de las estrellas. La afirmación de que incluso la más cercana de ellas está a una distancia de 25.000.000 millones de millas [40.233.600 millones de km] difícilmente transmite una imagen definida a la mente, pero puede que nos vaya mejor [ p. 37 ] con la afirmación alternativa de que la distancia es de 4,27 años luz, es decir, la distancia que la luz, viajando a 186.000 millas por segundo [299.338 km/s], tarda 4,27 años en recorrer.

La luz viaja a la misma velocidad que las señales inalámbricas porque ambas son ondas de perturbación eléctrica. Por cierto, esta velocidad es casi un millón de veces la del sonido. La enorme disparidad en las velocidades del sonido y de las ondas eléctricas se pone de manifiesto vívidamente en el proceso ordinario de transmisión. Cuando un orador transmite desde Londres, su voz tarda más en viajar 3 pies [1 m] desde su boca hasta el micrófono como una onda de sonido, que en viajar 560 millas [901 km] más hasta Berlín o Milán como una onda eléctrica. Los oyentes inalámbricos en Australia escuchan la música de un concierto transmitido antes que un oyente común en la parte trasera de la sala de conciertos que depende únicamente del sonido; ellos lo escuchan una quinceava parte de un segundo después de que se toca. Sin embargo, la luz, u ondas inalámbricas que viajan a la misma velocidad que la luz, tarda 4,27 años en llegar a la estrella más cercana, de modo que los habitantes de Próxima Centauri tardarían más de cuatro años y un cuarto en escuchar un concierto terrestre. Y con el tiempo tendremos que considerar otras estrellas aún más distantes a las que la música terrestre aún no habría llegado si hubiera iniciado su viaje antes de la conquista normanda, antes de que se construyeran las pirámides, incluso antes de que apareciera el hombre en la tierra.
¶ La época fotográfica
Si sólo se nos permitiera seleccionar un hito más en el progreso de la astronomía, bien podríamos elegir la aplicación de la fotografía a la astronomía en los últimos años del siglo XIX; esto abrió las compuertas [ p. 38 ] del progreso más a fondo que cualquier otra cosa que se haya hecho desde la invención del telescopio. Hasta entonces, el telescopio, después de recoger y desviar los rayos de luz del cielo, había proyectado el haz concentrado de luz a través de la pupila del ojo humano sobre la retina; en el futuro fue para proyectarlo sobre la placa fotográfica incomparablemente más sensible. El ojo puede retener una impresión sólo por una fracción de segundo; la placa fotográfica suma todas las impresiones que recibe durante horas o incluso días, y los registra prácticamente para siempre. El ojo sólo puede medir distancias entre objetos astronómicos con la ayuda de una intrincada maquinaria de alambres cruzados, tornillos y verniers; la placa fotográfica registra distancias automáticamente. El ojo, traicionado por ideas preconcebidas, impaciencia o esperanza, puede cometer y comete todo tipo de errores concebibles; la cámara no puede mentir.
Y así sucede que si tratamos de seleccionar puntos de referencia en la astronomía del siglo XX encontramos que, en cierto sentido, consiste en nada más que puntos de referencia; los lentos y arduos métodos de conquista del siglo XIX han dado lugar a una especie de fiebre del oro en la que se replantean las concesiones, se rasca la superficie, se recogen las pepitas más visibles y se abandona la excavación por algo más prometedor, todo con tal rapidez que cualquier intento de describir la posición está desactualizado casi antes de que pueda imprimirse. Solo podemos intentar una impresión general del nuevo territorio, y con esto se mezclará inextricablemente una discusión del antiguo territorio visto a la luz del nuevo conocimiento.
[ p. 39 ]
¶ Grupos de estrellas y sistemas binarios
Una mirada al cielo, o mejor, a una fotografía de un fragmento del cielo, sugiere que, en general, las estrellas están dispersas al azar sobre el cielo, excepto por la concentración de estrellas débiles en y hacia la Vía Láctea, que ya hemos considerado. Cualquier pequeña parte del cielo no se ve muy diferente de lo que se vería si estrellas brillantes y débiles hubieran sido rociadas al azar de un pimentero celestial.
Sin embargo, esta no es toda la historia. Aquí y allá se ven grupos de estrellas visibles, que difícilmente pueden haberse juntado por pura casualidad. El cinturón de Orión, las Pléyades, el cabello de Berenice, incluso la misma Osa Mayor, no parecen accidentes, y de hecho no lo son. Es la existencia de estos grupos naturales de estrellas lo que se encuentra en la raíz y justifica la división de las estrellas en constelaciones. Más adelante explicaremos cómo se estudian las propiedades físicas de las estrellas; por ahora es suficiente señalar que el estudio físico confirma la sospecha de que grupos como los que acabamos de mencionar son, en general, verdaderas familias, y no meros concursos accidentales, de estrellas. Las estrellas de cualquier grupo, como las Pléyades, no solo muestran las mismas propiedades físicas, sino que también tienen movimientos idénticos a través del espacio, viajando perpetuamente a través del cielo en la sociedad de los demás. Como ese grupo de estrellas son físicamente similares y viajan en compañía, podrían describirse apropiadamente como una familia de estrellas. El astrónomo, sin embargo, prefiere llamarlos «cúmulos en movimiento».
Estas familias son de casi todos los tamaños, las más pequeñas [ p. 40 ] y las más comunes constando de solo dos miembros. Después de esto, el siguiente tipo más común consta de tres miembros; nuestros tres vecinos más cercanos en el espacio, Proxima Centauri y las dos estrellas de Centauri, forman un sistema triple de este tipo. Luego vienen los sistemas de cuatro, cinco y seis miembros, y así indefinidamente.
En primer lugar, dirijamos nuestra atención a las familias que constan de solo dos miembros: los «sistemas binarios», como generalmente se les llama. Incluso si las estrellas se hubieran rociado al azar en el cielo con un pimentero, las leyes del azar exigirían que, en un cierto número de casos, los pares de estrellas aparecieran muy juntos. Y un estudio de una fotografía de cualquier campo de estrellas muestra que realmente existe un gran número de pares tan cercanos. Sin embargo, el número es mayor de lo que puede explicarse únicamente por las leyes del azar. Algunos pares de estrellas pueden estar juntos por accidente, pero se necesita una causa física para explicar el resto. Podemos desentrañar el misterio fotografiando el campo a intervalos de algunos años y comparando los diversos resultados obtenidos. Se encontrará que algunas de las estrellas que originalmente aparecían como pares cercanos se separan constantemente. Estos son los pares de estrellas que, aunque aparecían juntas en el cielo, no lo estaban en el espacio; una estrella simplemente estaba casi exactamente en línea con la otra vista desde la tierra. Otras parejas no se rompen con el paso del tiempo; los dos componentes cambian sus posiciones relativas pero nunca se separan completamente. En el caso más simple de todos, se puede encontrar que una estrella describe una órbita aproximadamente circular alrededor de la otra, al igual que la tierra alrededor del sol y la luna alrededor de la tierra, y precisamente por la misma razón: la gravitación los mantiene juntos.
[ p. 41 ]
La ley de la gravitación. Deja caer una pelota de cricket de tu mano y caerá al suelo. Decimos que la causa de su caída es la atracción gravitacional de la tierra. De la misma manera, una pelota de cricket lanzada al aire no se mueve eternamente en la dirección en que fue lanzada; si lo hiciera, dejaría la tierra para siempre y viajaría al espacio. Se salva de este destino por la atracción gravitacional de la tierra que lo arrastra gradualmente hacia abajo, de modo que vuelve a caer a la tierra. Cuanto más rápido lo lancemos, más lejos viajará antes de que esto ocurra; una bola similar proyectada desde un arma viajaría muchas millas antes de ser arrastrada de regreso a la tierra.
La ley que gobierna todos estos fenómenos es bastante simple. Es que la atracción gravitacional de la tierra hace que todos los cuerpos caigan 16 pies hacia la tierra en un segundo [4,8 m/s]. Esto es cierto para todos los cuerpos que caen libremente, sin importar cómo se muevan; todo cuerpo que no está de algún modo sostenido contra la gravitación está 16 pies [4,8 m] más bajo al final de cualquier segundo de lo que habría estado si la gravitación no hubiera actuado durante ese segundo.
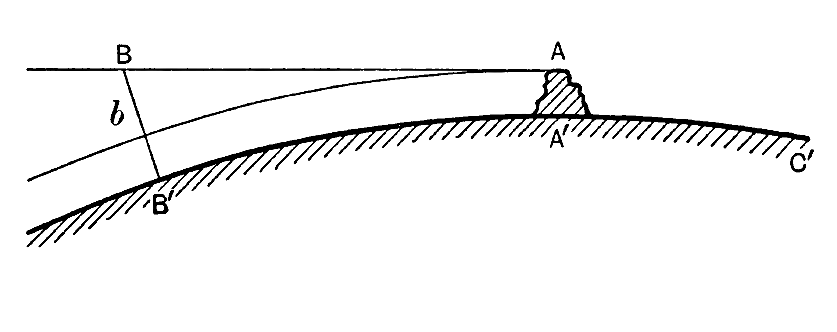
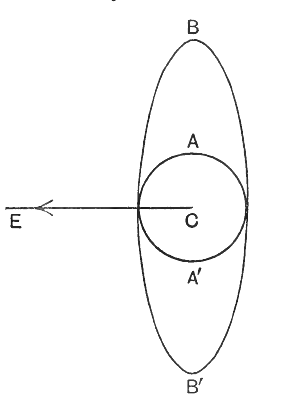
Para ilustrar lo que esto significa, dejemos que la gran curva circular B’A’C en la fig. 2 represente la superficie de la tierra, e imagina que se dispara un tiro horizontalmente desde A, la parte superior de una elevación AA’. Si la bala no fuera atraída hacia la Tierra por la gravedad, viajaría indefinidamente [ p. 42 ] a lo largo de la línea AB hacia el espacio. Si AB es la distancia que recorrería en un segundo en estas condiciones imaginarias, el final de un segundo de vuelo real no lo encuentra en B, sino en un punto 16 pies [4,8 m] más cerca de la tierra, habiéndolo atraído la gravedad hacia abajo durante su recorrido. Por ejemplo, si BB’ en la fig. 2 fuera de 16 pies [4,8 m], el disparo golpearía la tierra en B’ después de un vuelo de exactamente un segundo.
En otro ejemplo, supongamos que la caída de 16 pies [4,8 m] por debajo de B no arrastra el disparo hacia la tierra, sino solo hasta un punto b, que está precisamente a la misma altura sobre la superficie terrestre que el punto A en el que comenzó el disparo. Si no actuara la gravitación, de modo que el proyectil viajara a lo largo de la línea AB, su altura sobre la tierra aumentaría continuamente. En realidad, en el caso que ahora estamos considerando, la gravedad empuja el proyectil hacia abajo a una velocidad tal que neutraliza el aumento de altura que de otro modo ocurriría, de modo que la altura del proyectil ni aumenta ni disminuye; ni vuela al espacio ni cae a la tierra, sino que continúa describiendo círculos alrededor de la tierra indefinidamente.
Un cálculo geométrico simple muestra que para que la distancia Bb sea de 16 pies [4,8 m], la distancia recorrida por AB en un segundo debe ser de 25.880 pies o 4,90 millas [7,9 km] [2]. Así, si pudiéramos disparar un tiro horizontalmente con una velocidad de 4,90 millas por segundo [7,9 km/s], describiría círculos interminables alrededor de la tierra, la atracción gravitatoria de la tierra neutralizando exactamente la tendencia natural del tiro a volar a lo largo de la línea recta AB.
En 1665, Newton comenzó a sospechar que esta misma atracción gravitacional podría ser la causa de que la luna [ p. 43 ] describa una órbita circular alrededor de la tierra en lugar de huir por la tangente hacia el espacio. La distancia de la luna al centro de la tierra es de 238.857 millas [3.844.403 km], o 60,27 veces el radio de la tierra. Como la luna describe un círculo de este tamaño cada mes (27 días, 4 horas, 43 minutos, 11,5 segundos), podemos calcular que su velocidad en su órbita es de 2287 millas por hora [3.680 km/h]. Después de un segundo, habrá viajado 3350 pies [1021 m], y si mantuviera un curso estrictamente rectilíneo, esto lo alejaría 0.0044 pies de la tierra [1 mm]. Por lo tanto, para mantenerse en una órbita circular exacta alrededor de la Tierra, debe caer 0,0044 pies [1 mm] en un segundo. Esto es mucho menos que un cuerpo que cae en un segundo a la superficie de la tierra, pero Newton conjeturó que la fuerza de la gravedad debe debilitarse a medida que nos alejamos de la superficie de la tierra. En realidad, un cuerpo en la superficie de la tierra cae 3632 veces más rápido que la caída de la luna hacia la tierra en su órbita. Ahora bien, 3632 es el cuadrado de 60,27 (o 3632 = 60,27 x 60,27), de donde Newton vio que la caída de la Luna sería exactamente la cantidad correcta si la fuerza de gravedad cayera como [ p. 44 ] inverso al cuadrado de la distancia, es decir, si disminuye tan rápido como aumenta el cuadrado de la distancia. Como veremos más adelante, la observación astronómica confirma la verdad de esta ley de innumerables formas.
El profesor C. V. Boys y otros han medido la atracción gravitatoria que ejercen unas cuantas toneladas de plomo en el laboratorio y, con este conocimiento, es fácil calcular cuántas toneladas debe contener la tierra para ejercer su atracción gravitatoria observada sobre los cuerpos exteriores a ella. Se encuentra que el peso de la tierra debe ser algo menos de seis mil trillones de toneladas[3], o, como lo escribiremos, 6 x 1021 toneladas[4].
Así como la atracción gravitatoria de la Tierra mantiene a la Luna describiendo círculos a su alrededor perpetuamente, la atracción gravitatoria del Sol mantiene a la Tierra y a todos los demás planetas describiendo círculos alrededor del Sol. Conociendo la distancia de cualquier planeta al sol, y también su velocidad en su órbita, podemos calcular la distancia que cae este planeta hacia el sol en un segundo. Esto nos dice la cantidad de atracción gravitatoria del sol y, a partir de esto, podemos calcular que el peso del sol debe ser [ p. 45 ] alrededor de 332.000 veces el peso de la tierra, o casi exactamente 2 x 1027 toneladas. Cualquiera que sea el planeta que utilicemos, obtenemos exactamente el mismo peso para el sol. Esto no solo nos da confianza en nuestro resultado, pero incidentalmente también proporciona una sorprendente confirmación de la verdad de la ley de gravitación de Newton, porque si esta ley fuera inexacta o falsa, los diferentes planetas no contarían todos exactamente la misma historia en cuanto al peso del sol. Einstein ha demostrado recientemente que la ley no es absolutamente exacta, pero la cantidad de inexactitud es inapreciable excepto para el planeta más cercano, Mercurio, e incluso aquí es tan extremadamente pequeña que no necesitamos preocuparnos por ella para nuestro propósito actual.

Así como podemos pesar el sol y la tierra estudiando el movimiento de un cuerpo atrapado por su atracción gravitacional, o «en sus campos gravitatorios», como diría el matemático, podemos pesar cualquier otro cuerpo que mantenga un segundo cuerpo pequeño en movimiento a su alrededor por su atracción gravitatoria. Los movimientos de los satélites de Júpiter hacen posible pesar a Júpiter; se encuentra que su peso es de aproximadamente 1,92 x 1024 toneladas, que es 317 veces el de la tierra, aunque sólo 1/1047 del sol. De manera similar, se encuentra que el peso de Saturno es de 5,71 x 1023 toneladas o aproximadamente 94,9 veces el de la Tierra.
Pesando las estrellas. Y ahora llegamos a una sorprendente aplicación de los principios que acabamos de explicar: cuando observamos dos estrellas en el cielo que describen órbitas una alrededor de la otra, podemos pesar las estrellas a partir de un estudio de sus órbitas. Generalmente el problema no es tan simple como los que acabamos de discutir. Para su adecuado tratamiento, hay que volver a cobrar peaje a la obra matemática de Newton.
Hemos visto que un proyectil disparado horizontalmente con una velocidad de 4,90 millas por segundo [7,9 km/s], describiría [ p. 46 ] círculos interminables alrededor de la tierra. ¿Qué pasaría si se disparara en otra dirección y con otra velocidad?
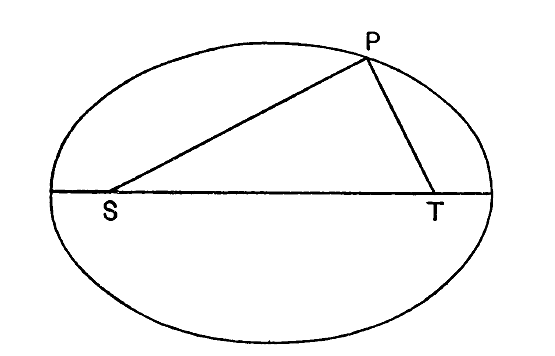
La respuesta fue proporcionada por Newton. Demostró que cuando se permite que un cuerpo pequeño se mueva libremente bajo la atracción gravitacional de un cuerpo grande, huirá por completo si su velocidad excede una cierta cantidad crítica, en cuyo caso su órbita es la curva llamada hipérbola. Pero si su velocidad es menor que esta cantidad crítica, su órbita siempre será una elipse, una especie de círculo extruído o una curva ovalada[5] (fig. 4, p. 47). Antes de esto, Kepler había descubierto que las trayectorias reales de los planetas alrededor del sol no eran círculos exactos sino elipses, aunque en su mayor parte elipses que no diferían mucho de los círculos; son lo que el matemático llama «elipse de pequeña excentricidad». Esto proporciona aún más confirmación de la ley de gravitación de Newton, ya que se puede demostrar que si la fuerza de gravitación cae de cualquier [ p. 47 ] otro modo que según la ley de Newton del inverso del cuadrado de la distancia, las órbitas de los planetas no serán elípticas.
Cuando el astrónomo estudia los movimientos de una estrella binaria en el cielo, generalmente encuentra que los dos componentes no se mueven en círculos uno alrededor del otro sino en elipses[6]. Una vez más, se confirma la ley de Newton, y tenemos derecho a suponer que las fuerzas que mantienen unidas a las estrellas binarias son las mismas fuerzas gravitatorias que impiden que la luna se aleje de la tierra, o los planetas del sol. Mediante un estudio de estas elipses se hace posible pesar las estrellas. Si una de las masas componentes fuera enormemente más pesada que la otra, la primera permanecería inmóvil mientras que la componente más ligera describiría una elipse a su alrededor, siendo el movimiento esencialmente similar al de un planeta alrededor del sol. Tales casos no se observan en estrellas binarias reales porque los dos componentes son generalmente comparables en peso, y esto trae nuevas complicaciones a la cuestión. No es necesario ingresar en [ p. 48 ] detalles matemáticos aquí. Baste decir que ninguna estrella se detiene; los dos componentes describen elipses de diferentes tamaños y, a partir del estudio de estas dos elipses, se pueden determinar los pesos de ambos componentes.
La siguiente tabla muestra el resultado de pesar los cuatro sistemas binarios más cercanos al sol de esta manera, tomando el peso del sol como unidad:
| Estrella | Distancia en años luz del sol |
Pesos de componentes en términos del peso del sol |
Luminosidad (ver p. 49) |
|---|---|---|---|
| Centauro A | 4,31 | 1,14 | 1,12 |
| „ B | 0,97 | 0,32 | |
| Sirio A | 8,65 | 2,45 | 26,3 |
| „ B | 0,85 | 0,0026 | |
| Proción A | 10,5 | 1,24 | 5,5 |
| „ B | 0,39 | 0,00003 | |
| Kruger 60A | 12,7 | 0,25 | 0,0026 |
| „ B | 0,20 | 0,0007 |
Vemos que los pesos de estas estrellas no difieren mucho de los del sol, aunque naturalmente todo el espacio proporciona un rango mayor que las cuatro estrellas de nuestra tabla que están cerca del sol. Pero incluso en todo el espacio, ninguna estrella cuyo peso se conoce con precisión tiene un peso menor que Kruger 60 B, aunque en el otro extremo de la escala hay muchas estrellas con pesos mucho mayores que cualquiera de nuestra tabla. De las estrellas cuyos pesos se conocen con bastante precisión, la estrella HD 1337 (estrella de Pearce) es la más pesada, sus dos componentes son respectivamente 36,3 y 33,8 veces más pesadas que el sol. La estrella de Plaskett B.D. 6° 1309 es ciertamente más pesada aún, sus [ p. 49 ] componentes pesando al menos 75 y 63 veces más que el sol, y probablemente más; los pesos exactos no se conocen (ver p. 55 abajo). El sistema 27 Canis Majoris consta de cuatro estrellas, cuyo peso combinado, según la evidencia actualmente disponible, parece ser al menos 940 veces mayor que el del sol, pero debemos tener cierta precaución antes de aceptar una cifra tan fuera de la habitual de pesos estelares.
La estrella constituyente promedio en la breve tabla anterior tiene 0,94 veces el peso del sol, de modo que nuestro sol parece tener un peso superior al promedio, y esto se confirma mediante un estudio más extenso de los pesos estelares.
Podríamos haber esperado a priori que las estrellas probarían tener todo tipo de pesos, porque no hay una razón obvia por la que las estrellas no deberían existir con pesos millones de veces mayores que los del sol, o de nuevo con pesos solo iguales a los de la tierra, o menos. En realidad, encontramos que los pesos de las estrellas son en su mayoría bastante iguales, muy pocas estrellas tienen pesos muy diferentes a los del sol. Esto parece indicar que una estrella es una especie definida de producto astronómico, no un mero trozo aleatorio de materia luminosa.
Luminosidad. La última columna de la tabla en la p. 48 da las «luminosidades» de las estrellas, lo que significa su potencia de candela como luces, siendo tomada la del sol como unidad. Por ejemplo, la entrada de 26,3 para Sirio significa que Sirio, considerado como un faro en el espacio, tiene 26,3 veces la potencia de candela del sol. Las luminosidades de las estrellas muestran un rango enormemente mayor que sus pesos. En general, se encuentra que las estrellas más pesadas son las más luminosas, como naturalmente deberíamos esperar, pero su luminosidad no guarda proporción con su peso. El componente más pesado de Sirius tiene solo 2,9 [ p. 50 ] veces el peso del componente más ligero, pero 10.000 veces su luminosidad. Nuevamente, en el sistema de Procyon, el componente más pesado tiene 3,2 veces el peso, pero 180.000 veces la luminosidad del componente más ligero. Parece ser una ley casi universal que la potencia de candela por tonelada es mucho mayor en las estrellas pesadas que en las ligeras. Este es uno de los hechos centrales y, a primera vista, uno de los más desconcertantes de la astronomía física: es tan fundamental y tan penetrante que no se puede aceptar ningún punto de vista del mecanismo estelar que no lo explique.
Velocidades espectroscópicas. Cuando se conoce la distancia de una estrella, su movimiento a través del cielo nos dice su velocidad en una dirección en ángulo recto con la línea a lo largo de la cual la miramos, es decir, a través de la línea de visión, pero no proporciona medios de descubrir su velocidad a lo largo de esta línea. No podemos ver el movimiento de un cuerpo que viene directamente hacia nosotros, y una estrella que se mueve a un millón de millas por segundo en una dirección exactamente a lo largo de la línea de visión parecería estar inmóvil en el cielo. Para evaluar las velocidades a lo largo de la línea de visión, el astrónomo pide la ayuda del espectroscopio.
Toda luz es una mezcla de luces de diferentes colores, y así como Newton, con su famoso prisma, analizó la luz del sol en todos los colores del arco iris, así el espectroscopio analiza la luz de una estrella, o de cualquier fuente, en su varios colores constituyentes. El instrumento dispersa la luz analizada en una franja de luz de color graduado continuamente, que se describe como un «espectro». En este los colores son los mismos, y se encuentran dispuestos en el mismo orden, como en el arco iris, que va del violeta al verde y del naranja al rojo. Hay una razón física para esto. Veremos más adelante (p. 114) que la luz [ p. 51 ] consiste en trenes de ondas, como las ondas que el viento sopla en un estanque, y que los diferentes colores de luz resultan de ondas de diferentes longitudes, la luz roja es producida por las ondas más largas y la luz violeta por las más cortas. Los colores del espectro aparecen en el orden de sus longitudes de onda, desde el más largo (rojo) hasta el más corto (violeta). En el espectro estelar típico, generalmente faltan ciertos rangos cortos de color o longitud de onda, por razones que discutiremos más adelante (p. 126), de modo que el espectro parece estar atravesado por una serie de líneas o bandas oscuras, formando así un patrón en lugar de una gradación continua de colores. En la Lámina VIII se muestran ejemplos de espectros estelares.

Con frecuencia es conveniente clasificar las estrellas por el tipo de espectros que emiten. Ahora se sabe que el espectro de una estrella depende principalmente de la temperatura de su superficie. Como consecuencia, los espectros estelares pueden, en general, organizarse en una sola secuencia continua, y su clasificación habitual es por una secuencia de letras, O, B, A, F, G, K, M con subdivisiones decimales, la temperatura cayendo a medida que avanzamos en la secuencia, de modo que las estrellas de tipo O tienen las temperaturas superficiales más altas y las estrellas de tipo M las más bajas. Los tipos espectrales se indican a la izquierda en la Lámina VIII.
Cuando la luz recibida de una estrella se analiza en un espectroscopio, se puede encontrar que el patrón de líneas o bandas se desplaza corporalmente en una dirección u otra. Si el desplazamiento es hacia el extremo rojo del espectro, la luz emitida por la estrella nos llega en un estado más rojo de lo que normalmente debería ser, y como la luz roja tiene la longitud de onda más larga, esto significa que cada onda de luz es más larga, más prolongada, de lo normal. Concluimos que la estrella se está alejando [ p. 52 ] de nosotros. De la misma manera, si el patrón espectral se desplaza hacia el extremo violeta del espectro, sabemos que la estrella debe estar acercándose a nosotros. El desplazamiento de un espectro resultante del movimiento del cuerpo que lo emite se describe generalmente como el «Efecto Doppler». A partir de su cantidad podemos calcular la velocidad real de una estrella a lo largo de la línea de visión, y el cálculo es sorprendentemente simple. Si se encuentra que cada línea o banda en un espectro representa una longitud de onda de una centésima parte del uno por ciento, más larga que la normalmente asociada con ella, entonces la velocidad de recesión de la estrella es una centésima parte del uno por ciento de la velocidad de la luz, o 18,6 millas por segundo [30 km/s], y de manera similar para todos los demás desplazamientos.
Binarios espectroscópicos. Como los dos componentes de un sistema binario generalmente se mueven con diferentes velocidades, el espectro normal de un sistema binario consta de dos espectros distintos superpuestos, los dos espectros muestran diferentes cambios que corresponden a las velocidades de los dos componentes. A partir de las órbitas observadas de los dos componentes de un sistema binario, un astrónomo podría proceder a calcular a qué velocidad se moverían estos componentes en la dirección de la línea de visión, y luego podría predecir en qué medida deberían desplazarse los dos espectros si la luz del sistema se analizó en un espectroscopio; el espectroscopio, por supuesto, confirmaría su predicción.
Es más instructivo imaginar el proceso inverso. Suponga que al analizar la luz de una estrella, el astrónomo obtiene un espectro compuesto en el que dos espectros distintos se desplazan rítmicamente hacia adelante y hacia atrás en torno a su posición normal. El hecho de que haya dos espectros le dice que se trata de un sistema binario; si el cambio rítmico se repite cada dos años, sabe que su órbita toma dos [ p. 53 ] años para completarse. Estudia la estrella por visión directa y descubre que es un sistema binario en el que los constituyentes giran unos sobre otros cada dos años.
Él examina otro espectro y descubre que cambia rítmicamente cada dos días. Al mirar directamente a esta estrella, solo puede ver un solo punto de luz. Debe haber, por supuesto, dos estrellas, pero el mero hecho de que den una vuelta alrededor de la otra en tan poco tiempo como dos días prueba que deben estar muy cerca una de la otra, y no debe sorprenderse de que su telescopio no haya logrado separar la imagen en dos puntos distintos de luz. Los sistemas de este tipo, que el espectroscopio muestra como binarios, pero que el telescopio suele mostrar como un único punto de luz, se denominan «binarios espectroscópicos». Se conocen más de mil de estos sistemas.
Si el astrónomo trata de construir la órbita de tal sistema a partir únicamente de las observaciones espectroscópicas, se encuentra en dificultades. Sus observaciones sólo le indican las velocidades a lo largo de la línea de visión, y éstas dependen tanto de la velocidad real como del grado de escorzo; la misma velocidad puede surgir de una gran órbita en un plano casi en ángulo recto con la línea de visión, o de una pequeña órbita muy acortada. Es imposible calcular la órbita real o los pesos de las estrellas solo a partir de la observación espectroscópica.
[ p. 54 ]
Binarios eclipsantes. Hay una excepción. Supongamos que se ve que la luz de una estrella disminuye en cantidad a intervalos regulares y luego vuelve a su intensidad original. La interpretación obvia de la disminución de la luz es que un componente del sistema está eclipsando al otro, y esto solo puede suceder si la órbita se acorta tanto que su plano pasa a través de la Tierra, o al menos muy cerca de ella. En tal caso, es posible reconstruir toda la órbita y, a partir de ahí, calcular los pesos de los dos componentes. No solo eso, sino que el tiempo durante el cual duran los eclipses nos dice los tamaños reales de los dos componentes, de modo que es posible dibujar una imagen completa del sistema. Los diagramas de las dimensiones y órbitas de dos binarios eclipsantes típicos se muestran en la fig. 6;
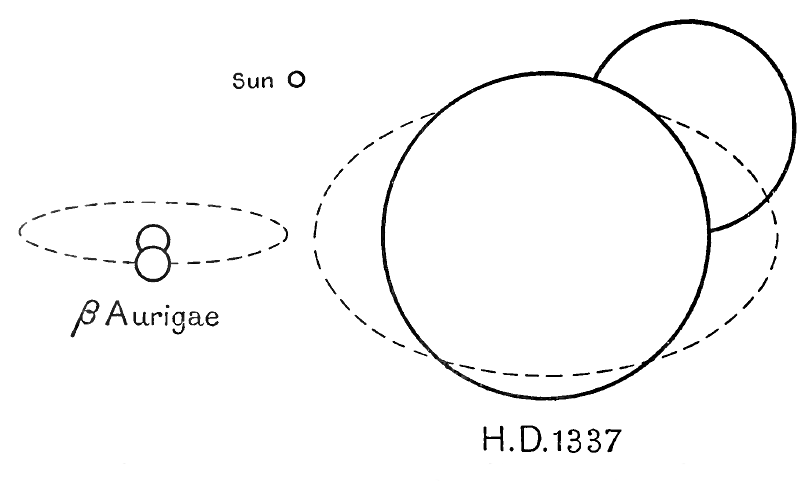
Cuando no ocurre ningún eclipse en un binario espectroscópico, no sabemos cuánto escorzo permitir, pero podemos obtener una idea general de los pesos de los [ p. 55 ] componentes suponiendo un grado medio de escorzo. Si asumimos diferentes grados de acortamiento a su vez, encontraremos que los pesos calculados salen menores cuando se supone que el plano de la órbita pasa a través de la tierra, es decir, cuando las órbitas se calculan como si el sistema fuera eclipsante. Así, aunque no podemos descubrir los pesos reales de los componentes de un binario no eclipsante, siempre podemos establecer los límites por encima de los cuales deben estar, a saber, los pesos calculados como si el sistema fuera eclipsante. De este modo, sabemos que los dos componentes de la estrella de Plaskett deben tener más de 75 y 63 veces el peso del sol.
¶ Estrellas variables
La mayoría de las estrellas brillan con una luz perfectamente estable, por lo que podemos decir que una estrella tiene tanto poder de candela. El sol, por ejemplo, emite una luz de 3,23 x 1027 candelas.
Sin embargo, hay clases de estrellas excepcionales en las que la luz parpadea hacia arriba y hacia abajo. En algunas, como en las binarias eclipsantes que acabamos de describir, las fluctuaciones de la luz son bastante regulares y se repiten con tal precisión que las estrellas bien podrían usarse como cronometradores. En otras, las fluctuaciones, aunque no perfectamente regulares, son casi regulares, mientras que existen otras en las que las fluctuaciones parecen ser completamente irregulares en la actualidad, aunque sin duda los cambios en estas se reducirán a la ley y el orden a su debido tiempo. Para nuestra presente discusión, los diversos tipos de variables irregulares no son de gran importancia.
Variables cefeidas. Las estrellas realmente interesantes son las de cierta clase de variables regulares, generalmente [ p. 56 ] llamadas «Variables cefeidas», por su prototipo δ Cefei. La naturaleza física de estas estrellas y el mecanismo de su fluctuación lumínica aún está lejos de comprenderse; las teorías en competencia están en un campo que no necesitamos discutir en esta etapa (ver p. 223 más abajo).
Cualquiera que sea su mecanismo, la observación muestra que estas estrellas poseen una cierta propiedad definida, que resulta ser de sumo valor. Siendo esto así, podemos aceptarlo con gratitud sin preocuparnos por su por qué y para qué. Las fluctuaciones de luz perfectamente regulares de las binarias eclipsantes las harían adecuadas como cronómetros, aunque no entendiéramos el mecanismo detrás de estas fluctuaciones. De la misma manera, las fluctuaciones de las variables cefeidas tienen una cualidad que las hace valiosas como varas de medir con las que estudiar las partes distantes del universo. En resumen, esta propiedad es que podemos deducir el brillo intrínseco de estas estrellas, y por lo tanto sus distancias, a partir de sus fluctuaciones de luz observadas.
Las fluctuaciones de luz son tan distintivas que hacen que las estrellas sean fáciles de detectar. Hay un rápido aumento de la luz, seguido de una lenta y gradual disminución; luego de nuevo el mismo rápido aumento y lento declive que antes. Es como si alguien arrojara brazadas de combustible a una hoguera a intervalos perfectamente regulares.
Otra clase de estrellas variables, generalmente conocidas como «variables de período largo», muestran fluctuaciones de luz algo similares, pero las dos clases se distinguen fácilmente por sus períodos muy diferentes de fluctuación de luz. La variable Cefeida completa su ciclo en un tiempo que puede ser de unas pocas horas, o puede ser de días o semanas, pero nunca más de un mes, mientras que la variable de período largo generalmente requiere alrededor de un año.
[ p. 57 ]
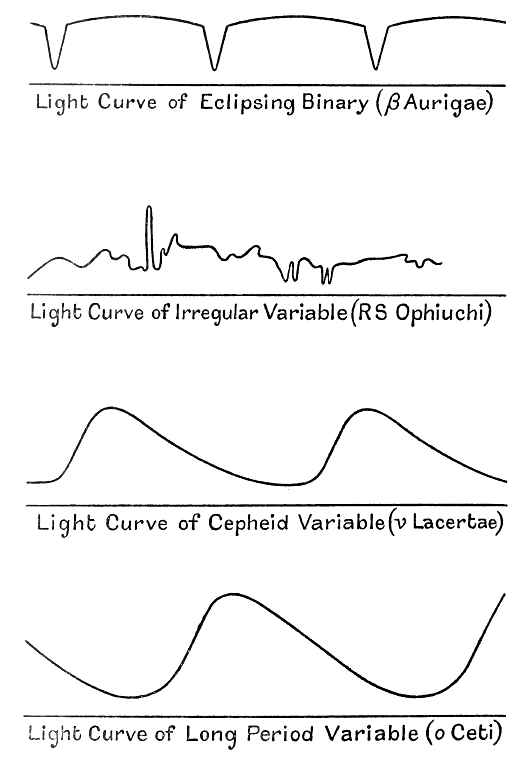
La Fig. 7 muestra las curvas de luz de estrellas variables típicas de las diferentes clases. En cada diagrama, el progreso del tiempo está representado por el movimiento a través de la página de izquierda a derecha; cuanto más alta esté la curva fluctuante por encima de la línea horizontal en cualquier instante, más brillante será la estrella en ese instante.
Cerca del límite del sistema galáctico hay un cúmulo de estrellas conocido como la Nube Menor de Magallanes Lámina XXI, p. 214), en la que las variables Cefeidas aparecen con gran profusión. En 1912, la señorita Leavitt de Harvard descubrió que la luz de las Cefeidas más brillantes en esta nube fluctuaba más lentamente que la luz de las más débiles. Cualquiera que fuera el responsable de encender y apagar las luces estelares, actuó más rápidamente para las luces débiles que para las brillantes. Por supuesto, el brillo aparente de varias Cefeidas a distancias variables dependería solo en parte de su brillo intrínseco o de la potencia de candela, pero las estrellas en la Nube de Magallanes están todas, casi lo suficientemente, a la misma distancia de la Tierra. Por tanto, las diferencias en los brillos aparentes de las estrellas en esta nube deben representar diferencias reales de brillo intrínseco, y este descubrimiento de Miss Leavitt podría expresarse en la forma de que el período de fluctuación de la luz de una cefeida depende de la potencia de candela. Aunque esto solo se demostró para las Cefeidas en la Nube de Magallanes, debe ser cierto para todas las Cefeidas dondequiera que estén, porque es inconcebible que podamos hacer que la luz de una estrella fluctúe más lenta o más rápidamente simplemente alterando su distancia de nosotros, al nosotros mismos alejarnos de ella, de hecho.
El profesor Hertzsprung de Leiden y el Dr. Shapley, entonces del Observatorio Mount Wilson, se apresuraron a aprovechar las implicaciones de este descubrimiento. Si se encuentran dos Cefeidas A, B en diferentes partes del cielo [ p. 59 ] fluctuando con la misma rapidez, entonces sus candelas intrínsecas deben ser iguales. Por lo tanto, cualquier diferencia en su brillo aparente debe atribuirse a una diferencia en sus distancias a nosotros. Si A parece cien veces más brillante que B, entonces B debe estar a diez veces la distancia de A. De la misma manera, una tercera Cefeida C puede resultar estar a diez veces la distancia de B. Ahora sabemos que C está cien veces más distante que A. Y si D puede encontrarse diez veces más distante que C, sabemos que D está mil veces más distante que A. Así podemos seguir construyendo y ampliando nuestra vara de medir; no hay límite hasta que alcanzamos distancias tan grandes que incluso las variables Cefeidas, que son estrellas excepcionalmente brillantes, se vuelven invisibles.
Hasta ahora solo hemos considerado las distancias comparativas de las Cefeidas. Sin embargo, las distancias absolutas de muchas de las Cefeidas más cercanas han sido determinadas por el método paraláctico ya explicado, es decir, midiendo su movimiento aparente en el cielo, resultante del movimiento de la tierra alrededor del sol. Tomando cualquiera de estas estrellas como nuestra Cefeida A original, podemos pasar continuamente de una Cefeida a otra, y así calcular las distancias absolutas de todas las variables Cefeidas en el cielo.
De esta manera, la relación observada entre el período de fluctuación y el brillo de las variables Cefeidas, comúnmente conocida como la «ley del período-luminosidad», puede proporcionar una escala en la que la luminosidad absoluta, o potencia de candela, de una Cefeida se puede leer directamente del período observado de sus fluctuaciones de luz. Las variables Cefeidas pueden considerarse como faros instalados en partes distantes del universo. Podemos reconocerlos, igual que un marinero [ p. 60 ] reconoce los faros, por la calidad de su luz. Podemos leer la potencia de candela a partir del período de sus fluctuaciones de luz observadas tan fácilmente como el marinero podría leer la potencia de candela de un faro en una carta del Almirantazgo. El brillo aparente de la Cefeida nos informa de la distancia que la separa de nosotros[7].
Sería difícil sobrestimar la importancia de todo esto para la ciencia astronómica moderna. Significa que se ha encontrado un método para inspeccionar, si no todo el universo, al menos aquellas partes del mismo en las que las variables cefeidas son visibles. En realidad, esta última reserva no es importante, ya que las variables Cefeidas están muy libremente dispersas en el espacio. Naturalmente, el método es de gran valor para la exploración de las partes más distantes del universo; aquí logra un éxito triunfal donde otros métodos fallan por completo. El método paraláctico comienza a fallar cuando intentamos sondear distancias de más de cien años luz. La trayectoria aparente en el cielo, que describe una estrella a esta distancia, como consecuencia del movimiento de la tierra alrededor del sol, es del tamaño de la cabeza de un alfiler de dos millas [3 km] [< small>p. 61] de distancia. Con todos sus refinamientos, a los instrumentos modernos les resulta bastante difícil detectar un movimiento tan pequeño como este, y es prácticamente imposible medirlo con precisión. La ley del «período-luminosidad» mide las distancias de los objetos hasta un millón de años luz de distancia, con un porcentaje de error menor que el esperado en las medidas paralácticas de estrellas a solo cien años luz de distancia.
¶ Espacio sonoro
Esto de ninguna manera agota la lista de métodos modernos de topografía del espacio. Cualquier tipo estándar de objeto astronómico, que sea fácilmente reconocible y emita la misma cantidad de luz sin importar dónde se encuentre, proporciona un medio obvio para medir distancias astronómicas, ya que una vez que se ha determinado la luminosidad intrínseca de tal objeto, la distancia de cada ejemplo de él se puede estimar a partir de su brillo aparente.
Las variables cefeidas de períodos asignados proporcionan el ejemplo más sorprendente de tales objetos estándar, pero hay otros tres disponibles, aunque generalmente no son tan útiles como las cefeidas. Primero viene otro tipo de estrella variable, las «variables de período largo» ya mencionadas, que son generalmente similares a las Cefeidas excepto que su luz fluctúa mucho más lentamente. Estas estrellas son intrínsecamente mucho más luminosas incluso que las Cefeidas, muchas de ellas son 10.000 veces más luminosas que el sol. En consecuencia, son visibles a enormes distancias y, en última instancia, se puede encontrar que proporcionan un medio para sondear las profundidades del espacio en las que incluso las cefeidas se pierden de vista.
Luego vienen las «novas» o nuevas estrellas. De vez en cuando, [ p. 62 ] una estrella ordinaria en el cielo estalla repentinamente en un resplandor de luz fenomenal, brillando con quizás mil veces su brillo original. La causa de estos estallidos violentos sigue siendo un tema de debate y aún no se ha dado una explicación completamente convincente. Sin embargo, un estudio de novas comparativamente cercanas ha proporcionado información sobre la luminosidad de la nova promedio cuando es más brillante, y como las novas aparecen en varias partes del cielo, y particularmente en las nebulosas extragalácticas, proporcionan un medio aproximado de medir distancias estelares y nebulosas.
Las estrellas azules proporcionan otro método más. Estas son extremadamente luminosas y varían muy poco en luminosidad intrínseca. Además, la luminosidad de cualquier estrella en particular generalmente se puede estimar con bastante precisión a partir de la calidad de la luz que emite, mediante métodos que se explicarán más adelante. Esto hace posible determinar las distancias de las estrellas azules y, por supuesto, de los objetos astronómicos en los que se encuentran.
Todavía pueden mencionarse brevemente otros dos métodos de un tipo diferente. El Dr. W. S. Adams, Director del Observatorio Mount Wilson, y otros han descubierto que ciertas peculiaridades definidas en los espectros de ciertas clases de estrellas transmiten información sobre el brillo intrínseco de la estrella que las emite; con esta información es fácil estimar la distancia de la estrella a partir de su brillo aparente. Esto se describe comúnmente como el método de paralaje espectroscópico.
Finalmente, se encuentra que la nube difusa de materia nebular que se esparce a través del espacio interestelar (p. 30) afecta la calidad de la luz que viaja a través de ella, de modo que el espectro de una estrella da una indicación de la cantidad de nube a través de la cual la luz de la estrella ha [ p. 63 ] viajado, y esto nuevamente proporciona un medio aproximado para estimar distancias dentro del sistema galáctico.

Cúmulos globulares. La ley de la luminosidad de las Cefeidas fue utilizada por primera vez por Hertzsprung para estimar la distancia de la Nube Menor de Magallanes, cuyo estudio había sido responsable del descubrimiento original de la ley. Posteriormente, Shapley lo utilizó para determinar las distancias de los misteriosos grupos de estrellas conocidos como «cúmulos globulares». Un ejemplo típico de estos se muestra en la Lámina IX. Se conocen alrededor de 100 de estos grupos y todos se parecen bastante, excepto por las diferencias en el tamaño aparente. Incluso estos últimos pueden atribuirse principalmente a diferencias de distancia, de modo que los cúmulos globulares son probablemente objetos casi idénticos, y la Lámina IX casi podría considerarse como una imagen de cualquiera de ellos. Las variables cefeidas abundan en todas ellas.
Shapley encontró el cúmulo globular más cercano, ω Centauri, a una distancia de unos 22.000 años luz, siendo el más lejano, NGC 7006, unas diez veces más remoto, a una distancia de 220.000 años luz. A tales distancias, el método paraláctico de medir distancias, por supuesto, fallaría irremediablemente. La órbita paraláctica de una estrella a 220.000 años luz de distancia es aproximadamente del tamaño de la cabeza de un alfiler mantenida a una distancia de 4000 millas [6.437 km]; ningún telescopio en la tierra podría detectar, y mucho menos medir, tal órbita.
La mera cifra de 220.000 años luz puede dar una idea muy pequeña de la distancia que nos separa de este cúmulo de estrellas, el más remoto. Podemos comprenderlo mejor si reflexionamos que la luz por la que vemos el cúmulo comenzó su largo viaje desde él hasta nosotros en algún momento en el que el hombre primitivo apareció por primera vez en la tierra. A través de la niñez, la juventud y la vejez de incontables generaciones de hombres, a través de las largas [ p. 64 ] edades prehistóricas, a través de los lentos albores de la civilización y a través de todo el lapso de tiempo que registra la historia, a través del ascenso y la caída de dinastías e imperios, esta luz ha viajado constantemente en su curso, cubriendo 186.000 millas por segundo [299.338 km/s], y apenas nos está alcanzando ahora. Y sin embargo, esta enorme extensión de espacio no nos lleva a los confines del universo; ahora veremos que con toda probabilidad apenas nos ha llevado a los confines del sistema galáctico.
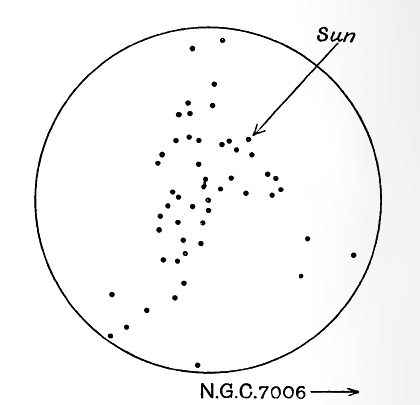
Shapley ha mapeado el sistema completo de los cúmulos globulares y encuentra que ocupan una región oblonga, situada a ambos lados del plano de la Vía Láctea, su mayor diámetro de unos 250.000 años luz encontrándose en este plano, y sus dos diámetros transversales considerablemente más cortos. El sol está más cerca del borde de esta región oblonga que de su centro, lo que explica por qué todos los cúmulos globulares aparecen en la mitad del cielo, como señaló Hinks por primera vez en 1911.
[ p. 65 ]
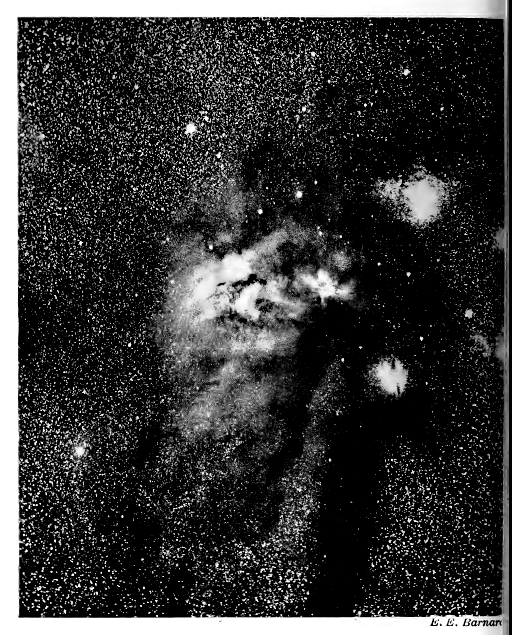
La disposición general se muestra en la fig. 8. La página del libro representa el plano de la Vía Láctea, los diversos puntos representan las posiciones en este plano que están más cerca de los diferentes cúmulos, de modo que el diagrama exhibe el sistema de cúmulos globulares como le parecería a un observador fuera en el espacio que viera el plano galáctico «de lleno». Todos los cúmulos globulares excepto NGC 7006 se encuentran dentro de un círculo de unos 125.000 años luz de radio, con su centro a unos 50.000 años luz del sol.
¶ El Arreglo Del Sistema Galáctico.
Aunque el asunto ha sido durante mucho tiempo objeto de una vigorosa controversia, ahora está quedando claro que la región del espacio trazada por estos cúmulos globulares coincide aproximadamente con la que ocupa el propio sistema galáctico. Herschel y Kapteyn parecen haber estado en un error al suponer que el centro del sistema galáctico está en la vecindad del sol; una acumulación considerable de evidencia indica que se encuentra en una nube estelar masiva en las constelaciones de Ofiuco y Escorpio. El Dr. Shapley y la Srta. Swope, del Observatorio de Harvard, han determinado recientemente que la distancia de esta nube estelar al sol es de 47.000 años luz, lo que la coloca casi exactamente en el centro del sistema de cúmulos globulares, como se muestra en la fig. 8. Existe lo que Shapley describe como un «sistema local» de estrellas bastante brillantes que rodean al sol, y el error de identificar esto con el sistema galáctico principal aparentemente ha sido responsable de gran parte de la confusión que hasta ahora ha acosado el problema de la arquitectura de la galaxia. Este sistema local tiene la misma forma aplanada que el sistema principal, pero no se encuentra exactamente en el plano de la Vía Láctea, ya que está inclinado en un ángulo de aproximadamente [p . 66] 12 grados. El sol parece estar muy cerca del plano central del sistema; determinaciones recientes lo sitúan a unos 100 años luz al norte de este plano. La Fig. 9 muestra una sección transversal del sistema, tal como ahora se imagina que se encuentra.
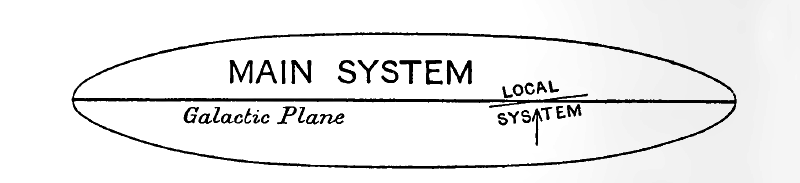
Ya hemos comparado la forma del sistema galáctico con la de una rueda. Obviamente, no podría conservar esta forma si las estrellas que la formaron estuvieran inmóviles en el espacio. Porque la atracción gravitacional de las estrellas internas haría que las estrellas más externas, el borde del rueda— cayeran hacia adentro, y el sistema terminaría como un revoltijo confuso de estrellas en algún lugar cercano al eje de la rueda. En 1913, Henri Poincaré, profesor de matemáticas en la Sorbona, sugirió que la «rueda» galáctica podría escapar a este destino si estuviera en estado de rotación. Así como el movimiento de la tierra evita que caiga sobre el sol, y el movimiento de la luna evita que caiga sobre la tierra, así, sugirió Poincaré, las estrellas que forman el borde de la rueda podrían salvarse de caer en el eje, mediante un movimiento de rotación de toda la rueda. Un cálculo aproximado sugirió que sería necesario que la rueda girara a razón de una revolución completa aproximadamente cada 500 millones de años.
Naturalmente, no es sencillo detectar una rotación tan lenta. Primero se sospechó que ocurría de la siguiente manera. Sabemos que cuando un trompo o [ p. 67 ] giroscopio se coloca en rotación rápida, se necesita una fuerza considerable para girar la parte superior del giroscopio en el espacio. Este es el principio de la brújula giroscópica, como la que se utiliza para dirigir los barcos. Un giroscopio, una especie de gran peonza de acero, comienza a girar con sus dos extremos girados en un marco oscilante. No importa cómo gire el barco, el movimiento del giroscopio mantiene el marco apuntando en la misma dirección y, con la ayuda de esta dirección fija, el barco se mantiene en su rumbo. Ahora bien, el sistema solar tiene muchas de las propiedades de un enorme trompo, las revoluciones de los planetas correspondientes al giro de la peonza. Como no hay ningún giro impreso en esta «peonza» desde el exterior, su eje de rotación debe apuntar siempre en la misma dirección, proporcionando así una especie de «brújula giroscópica» para orientarnos en el espacio.
En 1913, Charlier creyó haber descubierto que esta «brújula giroscópica» giraba contra el fondo distante de la Vía Láctea, a razón de una rotación completa cada 370 millones de años, un período que las mediciones posteriores aumentaron a 530 millones de años. Eddington luego sugirió que podría ser el fondo en lugar de la brújula giroscópica lo que estaba girando, la Vía Láctea en realidad giraba de la manera imaginada por Poincaré, y aproximadamente a la velocidad que Poincaré había calculado.
Investigaciones recientes de Oort, Plaskett, Lindblad y otros prueban sin lugar a dudas que tal rotación realmente ocurre, aunque no es del tipo simple de «rueda de carro» que hemos discutido hasta ahora. En el sistema solar, los planetas más interiores se mueven más rápidamente que los más exteriores: necesariamente deben hacerlo así si el movimiento de cada planeta ha de contrarrestar la atracción del sol. De la misma manera, si el movimiento de rotación de la galaxia [ p. 68 ] debe contrarrestar la atracción gravitacional de sus estrellas más internas, sus partes internas deben girar más rápidamente que las más externas. Así, el sol debería estar superando a las estrellas que se encuentran fuera de él en la rueda galáctica, mientras que él mismo es superado por las que se encuentran en su interior. Tal movimiento de adelantamiento es bastante fácil de detectar. Un análisis cuidadoso de los movimientos estelares observados ha revelado tal movimiento, mostrando que la galaxia como un todo está en rotación precisamente de la manera que acabamos de describir, las partes internas rotan más rápidamente.
El eje de esta gigantesca rueda se encuentra casi exactamente en la dirección que Shapley asignó al centro de la galaxia a partir de su estudio de los cúmulos globulares. Su distancia al sol, que aún no se puede determinar con gran precisión, es probablemente de unos 37.000 años luz. Dentro de los límites de precisión que actualmente son alcanzables, esto coloca el centro de la rueda galáctica en el centro del sistema de cúmulos globulares (ver fig. 8, p. 64). En la vecindad del sol, la rueda galáctica realiza una revolución completa en un período de unos 230 millones de años, y esto dota a las estrellas cercanas al sol de un movimiento a través del espacio a una velocidad de casi 200 millas por segundo [322 km/s], que surge de la rotación de la galaxia sola.
Con estos datos es posible pesar en masa las estrellas del sistema galáctico. Las estrellas individuales lejos del centro del sistema galáctico deben estar describiendo órbitas bajo la atracción gravitacional del sistema como un todo, la atracción que evita que las estrellas se dispersen en el espacio y, por lo tanto, mantiene el sistema galáctico en existencia. La suma de estos movimientos orbitales produce la rotación general de la galaxia que acabamos de discutir. Y a partir de las cifras que acabamos de mencionar, se puede calcular que el total del [ p. 69 ] peso de la materia dentro de la órbita del sol debe ser aproximadamente el de 240.000 millones de soles. Por supuesto, parte de esto puede surgir del polvo o gas interestelar. Sin embargo, como la estrella promedio pesa considerablemente menos que el sol, el número total de estrellas del sistema galáctico bien puede ser del orden de los 400.000 millones. Esta estimación, por supuesto, incluye todas las estrellas, tanto oscuras como luminosas, pero hay razones para creer que el número de estrellas oscuras es comparativamente pequeño (ver p. 269 más abajo).
Se han realizado otras estimaciones del número de estrellas de la galaxia, generalmente inferiores a las anteriores. Dos estimaciones de Lindblad, por ejemplo, dan el peso total de la galaxia en 110.000 y 180.000 millones de soles respectivamente.
De nuevo nos enfrentamos a la dificultad de visualizar números tan grandes. Con una vista perfecta en una noche clara y sin luna podemos ver unas 3000 estrellas. Imagine cada una de estas 3000 estrellas esparcidas en un cielo completo lleno de 3000 nuevas estrellas, y estamos contemplando 9 millones de estrellas, que todavía es solo el número visible en un telescopio de 5 pulgadas de apertura. Probablemente no podamos pedirle a nuestra imaginación que nos haga el mismo truco por segunda vez, pero si podemos persuadirla para que lo haga, y si podemos pensar en cada una de estas 9 millones de estrellas como generando nuevamente un cielo lleno de estrellas, todavía tenemos solo 27.000 millones de estrellas dentro de nuestro alcance, un número que todavía está muy por debajo de cualquier estimación permisible del número total de estrellas en el sistema galáctico. O nuevamente, notemos que el número de estrellas visibles fotográficamente en el telescopio de 100 pulgadas, es decir, 1500 millones, es aproximadamente igual al número de hombres, mujeres y niños en el mundo. Cada habitante de la tierra, cada [ p. 70 ] hombre, mujer y niño que viven en los cinco continentes o viajan por los siete mares, se les puede permitir elegir su propia estrella en particular, y luego pueden repetir el proceso decenas, y más probablemente cientos, de veces sin salir del sistema galáctico.
Después de esto, todavía podemos explorar fuera del sistema galáctico y encontrar más y más estrellas. El sistema galáctico, con sus cientos de millones de estrellas, no contiene más estrellas en el espacio que una casa contiene a todos los habitantes de Gran Bretaña. Hay millones de otras casas y millones de otras familias de estrellas.
Las Nebulosas Extra-Galácticas. Ya hemos hablado de los tenues objetos nebulosos que Herschel describió, un tanto conjeturalmente, como «universos islas». Estas son las otras casas en las que se encuentran otras familias de estrellas. Los más poderosos de los telescopios modernos muestran que consisten, al menos en parte, en enormes nubes de estrellas. Así como un poderoso microscopio muestra que una bocanada de humo de cigarrillo, a pesar de su apariencia de continuidad, consiste en una nube de partículas diminutas pero bastante distintas, un poderoso telescopio moderno descompone la luz de las regiones exteriores de estas nebulosas en distintos puntos de luz; la nebulosa se resuelve en una nube de partículas brillantes, al igual que la Vía Láctea en el diminuto telescopio de Galileo de hace tres siglos. La Lámina XI muestra un ejemplo; representa una ampliación de un área pequeña en la esquina superior izquierda de la Gran Nebulosa M 31 en Andrómeda ya mostrada en la Lámina IV (p. 30), y la resolución en distintos puntos de luz es inconfundible. Sabemos que al menos algunos de estos puntos de luz son estrellas, porque los reconocemos como variables Cefeidas, su luz muestra las inconfundibles [ p. 71 ] fluctuaciones características de las variables cefeidas familiares más cercanas a casa. Las otras partículas brillantes tienen un brillo comparable y muestran el rango de brillo por encima y por debajo del de las Cefeidas que se necesita para justificarnos al suponer que son estrellas ordinarias.


A partir de los períodos observados de fluctuación de sus variables Cefeidas, en combinación con los otros métodos que acabamos de explicar, el Dr. Hubble del Observatorio del Monte Wilson descubrió recientemente que incluso la más cercana de estas nebulosas, a saber, la nebulosa M 33 que se muestra en la Lámina XX (p. 213)), es tan remota que la luz tarda unos 850.000 años en viajar desde ella hasta nosotros. La Gran Nebulosa M 31 en Andrómeda (p. 30) está a una distancia ligeramente mayor de unos 900.000 años luz. Esto prueba abundantemente que estas nebulosas se encuentran justo fuera del sistema galáctico, lo que justifica el término nebulosas “extragalácticas”.
Se podría intentar estimar el número total de estrellas en estas nebulosas contando las visibles en un área pequeño promedio seleccionado, pero se dispone de métodos más precisos. Así como hemos supuesto que las estrellas más externas del sistema galáctico describen órbitas bajo la atracción gravitatoria de la galaxia como un todo, debemos suponer que las estrellas más externas de una nebulosa describen órbitas bajo la atracción gravitatoria de la masa principal de la nebulosa; las fuerzas que les impiden huir de la nebulosa son similares a las que mantienen a la tierra moviéndose en su órbita alrededor del sol. Si es así, podemos pesar las nebulosas, precisamente de la misma manera que pesamos el sol (p. 44) o el sistema galáctico (p. 69). El Dr. Hubble estima de esta manera que el peso de la Gran Nebulosa M 31 en Andrómeda, que se muestra en la Lámina IV, debe ser unas 3500 millones de veces la del sol, mientras que [ p. 72 ] la nebulosa NGC 4594 en Virgo, mostrada en la Lámina XV (p. 204), debe tener alrededor de 2000 millones de veces el peso del sol. En general, parece probable que cada una de las nebulosas extragalácticas contenga suficiente materia para formar unos 2000 millones de estrellas.
Esto no es lo mismo que decir que cada nebulosa ya contiene 2000 millones de estrellas. Si bien muchas de estas nebulosas parecen consistir principalmente en nubes de estrellas, la mayoría de ellas contienen también una gran región central que ningún poder telescópico ha logrado hasta ahora resolver en puntos distintos. Por ejemplo, la Lámina XII muestra la región central de la Gran Nebulosa en Andrómeda ampliada al mismo grado que la esquina superior izquierda que se muestra en la Lámina XI, y esto claramente no se resuelve en estrellas de la misma manera que las regiones exteriores que se muestran en la Lámina XI. Toda la nebulosa NGC 4594 en Virgo, mostrada en la Lámina XV, también se niega a ser dividida en estrellas separadas. Encontraremos razones más adelante (capítulo IV) para interpretar estas regiones centrales como masas de gas que están destinadas en el tiempo a formar estrellas, pero que aún no lo han hecho. De hecho, encontraremos que las nebulosas son los lugares de nacimiento de las estrellas, de modo que cada nebulosa consta de estrellas nacidas y estrellas aún no nacidas. Es el peso total de estrellas ya nacidas y de materia destinada a formar estrellas que suma 2000 millones de soles.
Alrededor de 2.000.000 de estas nebulosas extragalácticas son visibles en el gran telescopio de 100 pulgadas. En general, parecen estar dispersos con una tolerable aproximación a la uniformidad a través del espacio, su distancia media entre ellos es del orden de 2.000.000 de años luz, aunque aquí y allá esta uniformidad se ve interrumpida por nubes y cúmulos de nebulosas. Por ejemplo, el cielo es notablemente rico en nebulosas en las constelaciones de Virgo y Coma Berenices. Aquí se obtiene una nube de aproximadamente [ p. 73 ] 300 nebulosas, según Shapley, dentro de un espacio que tiene solo de 5 a 10 veces las dimensiones del sistema galáctico, a una distancia de unos diez millones de años luz del sol. La misma región del cielo parece contener también otras tres nubes más remotas. Shapley ha sugerido que nuestro sistema galáctico, la nebulosa de Andrómeda y otras nebulosas cercanas pueden constituir una nube similar.
Las profundidades más remotas del espacio. Hubble estima que la más distante de las 2.000.000 de nebulosas reveladas por el telescopio de 100 pulgadas [2,54 m] debe estar a unos 140 millones de años luz de nosotros. Esta es la mayor distancia que el ojo humano ha visto hasta ahora en el espacio. Los 220.000 años luz que formaban el diámetro del sistema galáctico parecían asombrosamente grandes al principio, pero ahora estamos hablando de distancias unas 600 veces mayores. Durante casi la 500ª parte de su largo viaje, la luz por la que vemos esta nebulosa visible, la más remota, viajó hacia una tierra deshabitada por el hombre. Justo cuando estaba a punto de llegar, el hombre llegó a existir en la tierra y construyó telescopios para recibirlo. Así al menos parece cuando se ve en la escala astronómica. Sin embargo, incluso esta última parte 500ª del viaje cubre la vida de 10,000 generaciones de hombres, a través de todos los cuales, así como durante un lapso de tiempo 500 veces mayor, la luz ha estado viajando constantemente hacia adelante a 186.000 millas por segundo [299.338 km/s].
Hay tantas nebulosas tenues en el límite mismo de la visión del telescopio de 100 pulgadas [2,54 m], que parece seguro que un telescopio aún mayor revelaría muchas más. El telescopio de 200 pulgadas [5 m], que se espera que se construya en breve, con el doble de apertura que el actual de 100 pulgadas [2,54 m], debería sondear el doble de distancia en el espacio, por lo que se puede esperar que muestre unas ocho veces más, o 16 millones, de nebulosas.
[ p. 74 ]
¶ La estructura del universo
Hasta ahora, cada aumento del poder telescópico nos ha llevado más y más profundo en el espacio, y el espacio parece expandirse a un ritmo cada vez mayor. Bien podemos preguntarnos si esta expansión está destinada a continuar para siempre: ¿hay algún límite en la extensión del espacio?
Incluso hace una generación, creo que la mayoría de los científicos habrían respondido negativamente a esta última pregunta. Habrían argumentado que el espacio podría estar limitado solo por la presencia de algo que no es espacio. Nosotros, o más bien nuestra imaginación, sólo podría ser impedido de viajar para siempre a través del espacio chocando contra una pared de algo diferente del espacio. Y, por difícil que sea imaginar que el espacio se extienda para siempre, es mucho más difícil imaginar una barrera de algo diferente del espacio que pueda impedir que nuestra imaginación pase a un espacio más allá.
El argumento no es sólido. Por ejemplo, la superficie de la tierra tiene una extensión limitada, pero no hay barrera que nos impida viajar tan lejos como queramos. Un viajero que no entendiera que la superficie de la tierra es esférica, naturalmente esperaría que los viajes cada vez más largos desde su hogar le abrieran para siempre nuevas extensiones de territorio en espera de ser exploradas. Sin embargo, como sabemos, necesariamente se reduciría en el tiempo a repetir sus propias huellas. Como resultado de su curvatura, la superficie terrestre, aunque ilimitada, tiene una extensión finita.
¶ La teoría de la relatividad
A través de su teoría de la relatividad, Einstein afirma haber establecido que el espacio también, aunque ilimitado, es finito en extensión. El volumen total de espacio en el [ p. 75 ] el universo es de cantidad finita así como la superficie de la tierra es de cantidad finita, y por la misma razón; ambos se doblan sobre sí mismos y se acercan. La analogía es válida y útil sólo mientras tengamos cuidado de comparar todo el espacio con la superficie de la tierra, y no con su volumen. El volumen de la tierra también es finito en cantidad, pero por razones muy diferentes. Un topo que cavara una y otra vez en la tierra en línea recta, llegaría con el tiempo a algo que no es tierra: emergería al aire libre; pero podemos seguir y seguir sobre la superficie de la tierra sin llegar nunca a nada que no sea la superficie de la tierra. Las propiedades del espacio son las de la superficie, no las del volumen, de la tierra.
Como consecuencia de que el espacio se repliega sobre sí mismo, un proyectil o un rayo de luz puede viajar eternamente sin salir del espacio hacia algo que no es espacio y, sin embargo, no puede continuar eternamente sin repetir sus propias huellas. Por esta razón es probable que la luz pueda viajar por todo el espacio y regresar a su punto de partida, de modo que si apuntamos un telescopio lo suficientemente potente en la dirección correcta en el cielo de medianoche, deberíamos ver el sol y sus vecinos en el espacio por la luz que haya hecho el circuito del universo. No deberíamos verlos como son ahora, sino como eran hace muchos millones de años. La luz que había salido del sol hace tanto tiempo habría recorrido casi todo el espacio y luego, justo cuando estaba a punto de completar el círculo, sería captado por nuestro telescopio en lugar de permitirle iniciar su segundo viaje alrededor del espacio.
Esta curvatura del espacio tiene otras funciones además de la que realiza a gran escala, la de limitar el volumen total del espacio. Antes del día de Einstein, las [ p. 76 ] curvaturas de las trayectorias de los planetas, las pelotas de cricket y los proyectiles en general se atribuyeron a la atracción de una «fuerza» de gravitación. La teoría de la relatividad descarta esta supuesta fuerza como una pura ilusión y atribuye las trayectorias curvas de los proyectiles de todo tipo a sus esfuerzos por mantener una trayectoria recta a través de un espacio curvo. Este espacio curvo no es, es cierto, el espacio ordinario del astrónomo. Es un espacio puramente matemático y probablemente totalmente ficticio, en el que el espacio de los astrónomos y el tiempo de los astrónomos están inextricablemente unidos y entran como socios iguales. Para ser absolutamente exactos, hay cuatro socios iguales. Los primeros tres son las tres dimensiones del espacio ordinario: longitud, ancho y alto, o, si lo preferimos, norte-sur, este-oeste y arriba-abajo. El cuarto es el tiempo ordinario medido de manera apropiada a la forma en que hemos medido nuestro espacio (un año de tiempo que corresponde a un año luz de espacio, etc.), y luego multiplicado por la raíz cuadrada de -1. Esta última multiplicación por la raíz cuadrada de -1 es, por supuesto, el rasgo notable de todo el asunto. Pues la raíz cuadrada de -1 no tiene existencia real; es lo que el matemático describe como un número «imaginario». Ningún número real puede multiplicarse por sí mismo y dar -1 como producto. Sin embargo, solo cuando el tiempo se mide en términos de una unidad imaginaria de años, existe una verdadera asociación equitativa entre el espacio y el tiempo. Esto muestra que la asociación igualitaria es puramente formal: no es más que una ficción conveniente del matemático. De hecho, si hubiera sido algo más, nuestra convicción intuitiva de que el tiempo es algo esencialmente diferente del espacio podría no haber tenido ninguna base en la experiencia y, por lo tanto, se habría desvanecido antes de ahora.
[ p. 77 ]
Estas complicaciones con respecto al tiempo no deben ocuparnos aquí; el punto esencial es que la teoría de la relatividad de Einstein enseña que el espacio finalmente se dobla sobre sí mismo como la superficie de la tierra, de modo que la cantidad total de espacio es finita.
La cosmología de Einstein. Según la teoría original de Einstein, las dimensiones del espacio están determinadas por la cantidad de materia que contiene. Cuanta más materia hay, menor debe ser el espacio, y viceversa; el espacio solo podría tener una extensión literalmente infinita si no contuviera materia alguna. En consecuencia, el problema de determinar la extensión del espacio se reduce al de determinar cuánta materia contiene. No tenemos forma de estimar cuánta materia puede existir fuera de esas regiones del espacio que están al alcance de nuestros telescopios, pero dentro de estas regiones la materia parece estar distribuida de manera bastante uniforme en forma de nebulosas extragalácticas.
A partir de los pesos conocidos de estos, Hubble estima que la densidad media de la materia en el espacio debe ser aproximadamente 1,5 x 10-31 veces la del agua. Suponiendo que la materia se distribuye con esta densidad por todo el espacio, incluidas aquellas partes que nuestros telescopios aún no han penetrado, podemos calcular con bastante certeza que el radio del espacio es de 84.000 millones de años luz, o 600 veces la distancia de la nebulosa más lejana visible. El viaje alrededor del espacio tomaría 500.000 millones de años luz, y si alguna vez nuestros telescopios nos muestran el sistema solar desde atrás, lo veremos como era hace 500.000 millones de años.
Por lo tanto, según la teoría original de Einstein, incluso los 140 millones de años luz que podemos recorrer con nuestros telescopios forman solo una pequeña fracción de todo el espacio, algo así como una parte en mil [ p. 78] millones. Hay mucho espacio aún por explorar. Quizás no sea sorprendente. La humanidad, que ha estado en posesión de telescopios durante sólo 300 años de los 300.000 de su residencia en la tierra, difícilmente podría esperar descubrir todo el espacio en tan poco tiempo. Nuestros exploradores astrónomos se mueven de isla en isla en el pequeño archipiélago que rodea su hogar en el espacio, pero todavía están lejos de circunnavegar el globo. Y, así como los primeros geógrafos trataron de estimar el tamaño de la tierra, mucho antes de que pensaran en circunnavegarlo, a partir de la curvatura de una pequeña parte de su superficie, así los astrónomos ahora están tratando de formar estimaciones, aunque necesariamente vagas, del tamaño de todo el universo a partir de la curvatura de esa parte de él con la que ya se conocen.
La teoría general de la relatividad ha superado hace tiempo la etapa de ser considerada como una especulación interesante. No solo da cuenta de los fenómenos del movimiento planetario ante los cuales falló la ley de gravitación de Newton, sino que predijo otros fenómenos: los desplazamientos aparentes de las estrellas cerca del Sol en un eclipse, como resultado de la curvatura de la luz por la que las vemos al pasar a través del campo gravitatorio del sol, y un cierto desplazamiento de los espectros estelares hacia el extremo rojo, que eran completamente insospechados cuando se hicieron las predicciones por primera vez, pero que posteriormente han sido completamente confirmados por la observación. De hecho, la teoría ya se ha calificado como una de las herramientas de trabajo ordinarias de la astronomía. Se ha utilizado para medir el diámetro de la pequeña y tenue estrella Sirio B, la compañera de Sirio (p. 262), así como discutir la naturaleza de las estrellas en los centros de las «nebulosas planetarias» (p. 323).
[ p. 79 ]
Sin embargo, la teoría general de la relatividad no conduce a la cosmología de Einstein de manera única. Es perfectamente posible que lo primero sea verdadero y lo segundo falso. La teoría general de la relatividad fija los atributos de cualquier pequeña fracción del universo de manera bastante definitiva, pero deja abiertas varias formas alternativas en las que estas pequeñas fracciones pueden juntarse para formar un todo. Por lo tanto, la particular visión del cosmos de Einstein no puede reclamar el prestigio que se atribuye a la teoría general de la relatividad en su conjunto. Y, de hecho, durante algunos años cayó algo en desgracia, y parecía probable que fuera reemplazada por una cosmología alternativa que De Sitter de Leiden propuso y desarrolló con cierto detalle en 1917.
La cosmología de De Sitter. Tratemos primero de entender las diferencias esenciales entre estas dos cosmologías.
La cosmología de Einstein supone que el tamaño del cosmos está determinado por la cantidad de materia que contiene. Si se decidió, en el momento de la creación, crear un universo que contuviera cierta cantidad de materia que debía obedecer a ciertas leyes naturales, entonces el espacio debe haberse ajustado de inmediato al tamaño adecuado para contener solo esta cantidad de materia y no más. O, si se decidió el tamaño del universo y las leyes naturales, la creación de cierta cantidad definida de materia se convirtió en una necesidad inevitable. El universo de De Sitter es menos simple o, si preferimos decirlo así, permite más libertad de elección en su creación. Una vez fijadas las leyes de la naturaleza, todavía era posible crear un universo de cualquier tamaño y poner en él cualquier cantidad de materia, dentro de ciertos límites. Visto desde el punto de vista estrictamente científico, el universo de Einstein tiene un elemento de arbitrariedad menos que el [ p. 80 ] universo de De Sitter, y en esta medida tiene la ventaja de la simplicidad.
Por otro lado, esta simplicidad se adquiere a un precio. La piedra angular fundamental de toda la teoría de la relatividad es la asociación equitativa de espacio y tiempo en el sentido ya explicado. La cosmología de Einstein gana su simplicidad sólo a expensas de suponer que esta igualdad de asociación desaparece cuando vemos el cosmos como un todo. Supone que el espacio y el tiempo son indistinguibles (en el sentido puramente formal ya indicado) sólo para un ser cuya experiencia se limita a una pequeña fracción del universo; se vuelven absolutamente distintos para un ser que puede recorrer todo el espacio y el tiempo. No está del todo claro cuánto peso debe atribuirse a esta objeción, si es que lo es. El espacio real y el tiempo real, sin duda, son distintos. Incluso si negamos la realidad de ambos, siguen siendo distinguibles como modos de percepción. ¿Qué reproche, pues, puede hacerse a una cosmología que admite que, en última instancia, cuando se contempla el universo a gran escala, el espacio y el tiempo se resuelven en distintos tipos de entidad? De alguna manera ya lo sabíamos, antes de que empezáramos a contemplar el universo a gran escala.
Cualquiera que sea la respuesta a esta última pregunta, la cosmología de De Sitter evita todo reproche posible al mantener la asociación igualitaria de espacio y tiempo, no solo en fracciones individuales del cosmos, sino en todo el cosmos como un todo. Por supuesto, se entenderá que todavía estamos hablando de una asociación igualitaria en el sentido puramente formal ya explicado, un año luz entrando en la cosmología en el mismo pie que la raíz cuadrada de -1 año. Incluso [ p. 81 ] la cosmología de de Sitter no pretende que un año luz (9,46 millones de millones de kilómetros) sea lo mismo que doce meses.
Aunque la principal teoría de la relatividad de Einstein ha sido ampliamente confirmada por la observación, su parte cosmológica no predijo ninguna característica especial como la que permite una prueba de observación directa. La cosmología de De Sitter, en cambio, predecía que los espectros de todos los objetos distantes debían mostrar un desplazamiento hacia el rojo, de cuantía dependiendo de la distancia del objeto. La asociación equitativa de espacio y tiempo da como resultado que las vibraciones de las ondas de luz emitidas por cualquier fuente específica sean más lentas en las partes distantes que en las cercanas del universo; la corriente del tiempo rueda más rápidamente donde nos encontramos que en cualquier otro lugar. Esto suena paradójico al principio, pero el examen muestra que no lo es; de Sitter no nos está pidiendo que regresemos a un universo geocéntrico, porque muestra que el habitante de una estrella lejana también encontraría que los átomos terrestres marcaban el tiempo más lentamente que los suyos. La paradoja queda completamente resuelta por el concepto de la relatividad de todas las medidas de espacio y tiempo.
Este desplazamiento hacia el rojo como resultado de la mera distancia es peculiar de la cosmología de De Sitter. Es adicional al desplazamiento que, como todas las cosmologías convienen, debe mostrar el espectro de un móvil como resultado de su movimiento, siendo este último hacia el rojo sólo si el cuerpo se aleja de la tierra (p. 51). En la cosmología de De Sitter, los dos desplazamientos no son completamente independientes, ya que es una característica esencial de esta cosmología que los cuerpos cercanos tiendan a alejarse más el uno del otro. Así como los pedazos de paja arrojados juntos a un arroyo tienden a [ p. 82 ] separarse a medida que flotan río abajo, así los objetos en el universo de De Sitter se separan más a medida que flotan río abajo en el tiempo.
De este modo, según la teoría de De Sitter, un desplazamiento de las líneas espectrales hacia el rojo no puede interpretarse como evidencia ni de movimiento ni de distancia; es una mezcla de ambos. Esto no significa que nos hayamos equivocado por completo al deducir las velocidades de las estrellas en el sistema galáctico a partir de los desplazamientos observados de sus líneas espectrales. Ningún desplazamiento apreciable se produce por la sola distancia, a menos que esta distancia forme una fracción apreciable del radio del universo. Desplazamientos sistemáticos al rojo se observan, es cierto, en los espectros de las estrellas más lejanas, pero son de muy pequeña cuantía. Solo cuando miramos a las nebulosas extragalácticas remotas podemos esperar observar el efecto con una fuerza apreciable.
Ahora bien, durante mucho tiempo ha sido uno de los enigmas sobresalientes de la astronomía que los espectros de las nebulosas distantes se desplazan uniformemente hacia el rojo. Los desplazamientos observados no son pequeños. Interpretados como velocidades, muchos de ellos representarían velocidades de más de 1000 millas por segundo [1609 km/s]. Humason ha descubierto que dos nebulosas débiles, NGC 4860 y 4853, muestran velocidades aparentes de recesión de 4900 y 4600 millas por segundo [7.885 y 7.403 km/s], respectivamente. Ambas son miembros de una nube de nebulosas en Coma Berenices (p. 72), que probablemente se encuentra a una distancia de unos 50 millones de años luz. Recientemente se ha encontrado que el espectro de otra nebulosa muy tenue en Ursa Major indica un aparente movimiento de recesión con una velocidad de 7200 millas por segundo [11.587 km/s]. Si se rechaza la teoría de De Sitter, casi todas las nebulosas extragalácticas deben estar huyendo de nosotros con terribles velocidades casi inimaginables. Y cuanto más lejos estén [ p. 83 ] tanto más precipitadamente aumentan su distancia. Sin embargo, difícilmente podemos reintroducir la simplicidad adoptando la teoría de De Sitter y tratando toda la aparente estampida de nebulosas como falsa, ya que esta teoría implica que las nebulosas bien pueden, de hecho, estar huyendo de nosotros, siendo la dispersión una propiedad inherente de los objetos en un universo de De Sitter.
El hecho de que los espectros de las nebulosas más distantes muestren estos grandes desplazamientos proporciona una cierta presunción a favor de la verdad de la cosmología de De Sitter; esto al menos los explica dos veces, mientras que ninguna otra cosmología los explica en absoluto. Si aceptamos tentativamente esta cosmología, entonces cada cambio espectral observado debe considerarse como la suma de dos partes, una que surge de la forma ordinaria de una recesión de la nebulosa y la otra que surge simplemente de su distancia.
Un estudio preliminar del Dr. Hubble ha demostrado que, en general, los desplazamientos espectrales son mayores para las nebulosas más distantes, y que sus cantidades son aproximadamente proporcionales a las distancias de las nebulosas a nosotros. Si interpretamos la totalidad de los desplazamientos observados simplemente como evidencia de recesión, podemos calcular que el radio del universo es de unos 2000 millones de años luz, o unas catorce veces la distancia de la nebulosa visible más lejana. Con un radio tan grande del universo, el desplazamiento adicional resultante de la mera distancia de nebulosas incluso remotas es insignificante, por lo que nuestra suposición de que los desplazamientos surgen casi por completo de las velocidades de recesión recibe una confirmación a posteriori. Si los desplazamientos observados de los espectros nebulares hubieran sido estrictamente proporcionales a sus distancias de nosotros, deberíamos haber obtenido una explicación consistente de los hechos observados [ p. 84 ] suponiendo que viviéramos en un universo de De Sitter con un radio de unos 2000 millones de años luz.
El Universo en Expansión. Solía pensarse que las cosmologías de Einstein y de Sitter eran antagónicas entre sí, ya que obviamente ningún universo podía ser un universo de Einstein y un universo de De Sitter al mismo tiempo. Una investigación reciente de un matemático belga, el abate G. Lemaitre, ha puesto un cariz diferente al problema. En resumen, Lemaitre ha demostrado que ningún universo podría permanecer permanentemente en el estado considerado por Einstein. Un universo en este estado es una estructura inestable; inmediatamente que comenzara a existir, comenzaría a expandirse, y no dejaría de expandirse hasta convertirse en un universo de De Sitter. Incluso después de esto, la expansión continuaría, pero ahora se fusionaría con la expansión normal del universo de De Sitter, como ya hemos considerado.
A la luz de estos resultados, la cuestión del problema no es si nuestro universo es un universo de Einstein o un universo de De Sitter, sino cuánto lleva recorriendo el camino que comienza con un universo de Einstein y termina con un universo de De Sitter. Cualquiera que sea la respuesta, nos lleva a suponer que al principio de los tiempos las nebulosas estaban mucho más cerca unas de otras de lo que están ahora, que desde entonces han obedecido a su tendencia inherente a dispersarse, o más bien a la tendencia del fluir corriente de tiempo para dispersarlos, y que ahora se están alejando de nosotros, y unos de otros, con velocidades que son proporcionales a sus distancias. Esto está de acuerdo con la conclusión de Hubble de que las velocidades aparentes de recesión de las nebulosas son aproximadamente proporcionales a sus distancias. A partir de los datos de Hubble Eddington ha calculado que el [ p. 85 ] universo original de Einstein debe haber tenido un radio de unos 1200 millones de años luz. Si se hubiera encontrado que las velocidades aparentes de recesión de las nebulosas eran estrictamente proporcionales a sus distancias, podríamos haber explicado todo suponiendo que vivimos en un universo en expansión, que había comenzado como un universo de Einstein de 1200 millones de años luz de radio, ahora se había expandido a algo del orden de 2000 millones de años luz de radio, y estaba destinado a seguir expandiéndose por toda la eternidad.
Esto proporciona una imagen simple y bastante fascinante del universo, pero hay muchas razones en contra de suponer que es verdadera. En primer lugar, si interpretamos los desplazamientos espectrales solo como evidencia de la velocidad, las velocidades de las nebulosas probablemente estén muy lejos de ser (como requeriría la imagen anterior) exactamente proporcionales a sus distancias de nosotros. Un grupo de tres nebulosas, que se cree que están a la misma distancia de unos 50 millones de años luz, difieren en casi 2000 millas por segundo [3218 km/s] en sus velocidades, que promedian unas 5000 millas por segundo [8.047 km/s]. Oort ha encontrado una tendencia general a que las velocidades de las nebulosas muy distantes no sean estrictamente proporcionales a sus distancias. A una distancia de 20 a 40 millones de años luz, las divergencias aparentes tienen un promedio de 750 millas por segundo [1.207 km/s], pero no está claro hasta qué punto estos resultan simplemente de estimaciones inexactas de las distancias de estas nebulosas remotas.
En segundo lugar, si los desplazamientos espectrales observados representan una mera dispersión, podemos calcular el tiempo transcurrido desde que comenzó esta dispersión; resulta ser muchos miles de millones de años. Por enorme que sea ese período de tiempo, no parece ser suficiente. Veremos más adelante (capítulo III) cómo el tiempo deja su huella, sus arrugas y sus canas, en las estrellas, de modo que podemos adivinar medianamente bien sus edades, y la evidencia [ p. 86] está toda a favor de vidas estelares, no de miles de millones, sino de millones de millones, de años. Si las nebulosas deben sus movimientos actuales a la mera dispersión, entonces las estrellas deben haber vivido la mayor parte de sus vidas antes de que comenzara esta dispersión. Tal hipótesis parece demasiado artificial para ser aceptada, en cualquier caso, siempre que quede abierta cualquier alternativa.
Por supuesto, debemos admitir francamente que nuestras estimaciones de las edades estelares pueden necesitar una revisión. De hecho, se han calculado sobre la suposición de que nunca ha tenido lugar una dispersión apreciable del tipo requerido por la cosmología de De Sitter. Si no solo las nebulosas, sino también las estrellas que componen el sistema galáctico, estuvieran agrupadas al principio de los tiempos, nuestras estimaciones de la vida de las estrellas tendrían que acortarse sustancialmente, y es concebible, aunque creo que muy poco probable, que podrían reducirse a longitudes del tipo que acabamos de considerar; ciertamente no podrían reducirse tanto si el universo original tuviera un radio cercano a la estimación de Eddington de 1200 millones de años luz.
Sin embargo, las cosmologías de De Sitter y Lemaitre requieren indudablemente que el universo actual debe estar en expansión, que las nebulosas deben estar retirándose unas de otras y de nosotros, y que sus espectros deben, en consecuencia, mostrar desplazamientos hacia el rojo. Pero no hay nada que nos obligue a identificar estos desplazamientos con los realmente observados. Muchas causas, además de los movimientos de recesión, son capaces de enrojecer las líneas espectrales, y sólo después de haber deducido todo el enrojecimiento debido a estas diversas otras causas estaremos en condiciones de decir que el residuo representa un verdadero movimiento de recesión.
Recientemente, el Dr. Zwicky de Pasadena sugirió [ p. 87 ] que la materia gravitante difundida a través del espacio puede enrojecer toda la luz que pasa a través del espacio. Da razones dinámicas para su sugerencia, calcula la cantidad de cambio espectral que se anticipa en la luz que nos llega desde las nebulosas y descubre que explicaría prácticamente la totalidad del cambio observado. Es posible que la mayor parte del enrojecimiento observado de la luz nebular se deba a esta o alguna causa similar, representando sólo una pequeña fracción los verdaderos movimientos de recesión. Si es así, podemos extender la edad del universo indefinidamente, y somos libres de asignar a las estrellas las edades muy grandes que la evidencia de la astronomía general parece exigir.
En la forma original de esta cosmología de De Sitter, la luz tardaría un tiempo infinito en viajar alrededor del universo, y esto evitaría que cualquier objeto fuera visto por la luz que había recorrido el camino más largo. Esto se debe a que de Sitter consideró solo el caso ideal de un universo completamente vacío de toda materia. Incluso con una pequeña cantidad de materia en el universo, el camino de un rayo de luz presumiblemente se doblaría sobre sí mismo y volvería a su punto de partida después de un tiempo finito. Se ha sugerido seriamente que dos nebulosas tenues (h 3433 y M 83) pueden ser en realidad nuestras dos vecinas más cercanas en el cielo, M 33 y M 31, vistas a lo largo del espacio. Si es así, vemos los frentes de dos objetos cuando miramos M 33 y M 31, y las espaldas de los mismos dos objetos cuando apuntamos nuestros telescopios exactamente en direcciones opuestas y miramos h 3433 y M 83. Sin duda, esto es solo una conjetura, y tal vez un poco descabellada, pero se han hecho muchas más conjeturas sorprendentes en astronomía, y posteriormente resultó ser cierto.
[ p. 88 ] Todas estas discusiones sobre la estructura del espacio son, por supuesto, altamente especulativas, pero concuerdan en sugerir la conclusión general de que, si aún no podemos ver la totalidad del espacio, podemos al menos inspeccionar una fracción apreciable de ella. Puede que nuestros astrónomos-exploradores aún no hayan circunnavegado el globo, pero tal vez estén descubriendo América, y bien podemos imaginar que incluso la próxima generación habrá completado la circunnavegación del espacio, y pensará en un espacio finito pero ilimitado en el mismo espacio de la misma manera, y con la misma facilidad, como pensamos en la superficie finita pero ilimitada de la tierra.
¶ Un modelo del universo
Encontramos bastante difícil visualizar los 4¼ años luz que constituyen la distancia a la estrella más cercana, por lo que se nos aconseja que ni siquiera intentemos visualizar esta última distancia de miles de millones de años luz, la circunferencia conjeturada del universo. Sin embargo, podemos tratar de ver todas estas distancias en proporción adecuada entre sí con la ayuda de un modelo dibujado a escala. Podemos escapar del esfuerzo de tratar de imaginar distancias inimaginablemente grandes manteniendo la escala muy pequeña.
La tierra, viajando 1200 veces más rápido que un tren expreso, hace un viaje de 600 millones de millas [965 millones km] alrededor del sol cada año. Representemos este viaje con una cabeza de alfiler 1⁄16 de una pulgada de diámetro [1,5 mm]. Esto fija la escala de nuestro modelo; el sol se ha reducido a una diminuta mota de polvo de de pulgada de diámetro [ mm], mientras que la tierra es una mota aún más diminuta que es demasiado pequeña para ser vista incluso en el más poderoso de los microscopios. En esta escala, la estrella más cercana en el cielo, [ p. 89 ] Proxima Centauri, debe colocarse a unas 225 yardas de distancia [205 m], y para contener incluso las cien estrellas más cercanas a nuestro sol en el espacio, el modelo debe tener una milla de alto, una milla de largo y una milla de ancho [4 km3].
Sigamos construyendo el modelo. Podemos pensar en las estrellas indistintamente como motas de polvo, porque sus tamaños varían tanto como los tamaños de las motas de polvo. En la vecindad del sol debemos colocar motas de polvo a distancias promedio de alrededor de un cuarto de milla entre sí [400 m]. En otras regiones del espacio, por lo general están aún más separados, ya que, debido a la presencia del «cúmulo local», la vecindad inmediata del sol resulta ser una parte del cielo bastante poblada. Continuamos construyendo el modelo a lo largo de cientos de millas en todas direcciones y luego, si estamos construyendo en una dirección muy alejada del plano galáctico, las motas de polvo comienzan a diluirse; nos acercamos a los confines de la galaxia. En el plano galáctico en sí mismo, construimos alrededor de 7000 millas [11.265 km] antes de llegar al cúmulo globular más lejano, y todavía estamos dentro del sistema galáctico. Con el largo viaje anual de nuestra tierra alrededor del sol como una cabeza de alfiler, todo el sistema galáctico tiene aproximadamente el tamaño del continente americano. Puede ser bueno hacer una pausa y tratar de visualizar los tamaños relativos de la cabeza de un alfiler y del continente americano, antes de continuar con la construcción de nuestro modelo mental.
Una vez que hayamos terminado el sistema galáctico, debemos viajar unas 30.000 millas [48.280 km] antes de comenzar a configurar la siguiente parte de nuestro modelo, al menos si lo mantenemos a escala. A esta distancia colocamos la siguiente familia de estrellas, una familia que probablemente sea sustancialmente más pequeña y más compacta que nuestra propia familia galáctica, pero que es comparable con ella tanto en tamaño como en número. Así que seguimos construyendo nuestro modelo: una familia de miles [ p. 90 ] de millones de estrellas cada 30.000 millas [48.280 km] más o menos, hasta que tengamos dos millones de esas familias. El modelo ahora se extiende por cerca de cuatro millones de millas [6,4 millones km] en todas las direcciones. Esto representa hasta dónde podemos ver en el espacio con un telescopio; podemos imaginar el modelo en marcha, aunque no sabemos cómo ni dónde; todo lo que sabemos es que la parte construida hasta ahora representa solo una fracción del universo.
Cada sistema galáctico o universo isla o nebulosa extragaláctica contiene miles de millones de estrellas, o materia gaseosa destinada en última instancia a formar miles de millones de estrellas, y sabemos de dos millones de tales sistemas. Hay, entonces, miles de millones de millones de estrellas dentro del rango cubierto por el telescopio de 100 pulgadas [2,5 m], y este número debe multiplicarse aún más para tener en cuenta las partes del universo que aún no han sido exploradas. En un cálculo moderado, el número total de estrellas en el universo debe ser algo así como el número total de motas de polvo en Londres. Piensa en el sol como algo menos que una sola mota de polvo en una gran ciudad, en la tierra como menos de una millonésima parte de esa mota de polvo, y quizás tengamos una imagen todo lo vívida que la mente puede realmente captar de la relación de nuestro hogar en el espacio con el resto del universo.
Un procedimiento alternativo habría sido construir nuestro modelo a escala tomando todas las motas de polvo de Londres y extendiéndolas a las distancias adecuadas para representar las diversas estrellas en el espacio. La distancia real promedio entre motas de polvo en Londres es una fracción bastante pequeña de pulgada; para que nuestro modelo tenga la escala correcta, esta distancia debe aumentarse a aproximadamente un cuarto de milla [400 m], incluso cuando estemos construyendo la parte que representa la parte poblada de espacio alrededor del sol. Si construimos nuestro modelo de esta manera, obtenemos [ p. 91 ] una vívida imagen del vacío del espacio. Vacíe la estación de Waterloo de todo excepto de seis motas de polvo, y todavía está mucho más llena de polvo que el espacio de estrellas. Esto es cierto incluso en la región relativamente poblada del interior del sistema galáctico; no tiene en cuenta los inmensos tramos vacíos entre un sistema de estrellas y el siguiente. Haciendo un promedio a lo largo de todo el modelo, la distancia media de una mota de polvo de su vecino más cercano resulta ser algo así como 80 millas [129 km]. El universo consiste principalmente no en estrellas, sino en un vacío desolado: extensiones inconcebiblemente vastas de espacio desértico en las que la presencia de una estrella es un evento raro y excepcional.
En la imaginación, tomemos una posición en el espacio en algún lugar cerca del sol, y observemos las estrellas moviéndose a una velocidad unas 1000 veces mayor que la de un tren expreso. Si el espacio estuviera realmente lleno de estrellas, nuestra posición sería tan poco envidiable como si nos sentáramos en medio de Regent Street para ver pasar el tráfico: nuestra vida, aunque emocionante, sería breve. Sin embargo, como muestra un cálculo exacto, el tráfico estelar está tan poco concurrido que tendríamos que esperar alrededor de un millón de billones de años antes de que una estrella se topara con nosotros. Expresado de otra forma, el cálculo muestra que cualquier estrella puede esperar moverse durante algo del orden de un millón de millones de años antes de chocar con una segunda estrella. Las estrellas se mueven a ciegas por el espacio, y los jugadores de la gallina ciega estelar son tan pocos y distantes entre sí que la posibilidad de encontrar otra estrella es casi insignificante. Veremos más adelante que este concepto es de la más profunda significación en nuestra interpretación del universo.
¶ Notas
Porque el brillo aparente de un objeto cae con el inverso del cuadrado de su distancia, y el cuadrado de 80.000 es aproximadamente igual a 6000 millones. ↩︎
Sea C el centro de la tierra y bCD el diámetro que pasa por b. Entonces BA2 = Bb x BD, donde Bb = 16 pies [4,8 m], y BD, que es 16 pies más que el diámetro de la tierra = 41.900.000 pies [12.771.120 m]. De esto fácilmente calculamos que BA = 25.880 pies [7888 m]. Este cálculo, por supuesto, desprecia la altura de la colina AA’ en comparación con el diámetro de la Tierra.
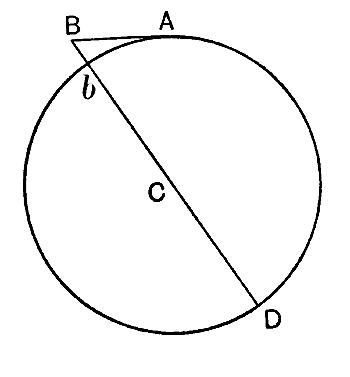 ↩︎
↩︎Aquí, como en todo el libro, usamos la tonelada métrica o francesa de un millón de gramos o 2204,5 libras. La tonelada inglesa de 2240 lbs. es igual a 10160 toneladas francesas. ↩︎
La notación 6 x 1021 representa el número formado por un 6 seguido de 21 ceros, siendo esta notación abreviada esencial, en aras de la brevedad, en la discusión de números astronómicos. Un millón es 106, un millón de millones es 1012 y así sucesivamente.
Se necesita una notación similar para expresar números muy pequeños. La expresión 10-21 se escribe para ello y así sucesivamente. Por tanto, 6 x 10-6 representa 6/1.000.000 o 0,000006. ↩︎La definición más simple de una elipse es que es la curva trazada por un punto móvil P que se mueve de tal manera que la suma de sus distancias PS, PT desde dos puntos fijos S, T permanece siempre igual. En la práctica, podemos dibujar una elipse más fácilmente deslizando una cuerda sin fin SPTS alrededor de dos chinchetas S, T clavadas en un tablero de dibujo. Estiramos la cuerda tensa con un lápiz en P, y dejando que el lápiz gire, manteniendo la cuerda siempre tensa, dibujaremos una elipse. Si los alfileres S, T en el tablero de dibujo se colocan cerca uno del otro, la curva descrita por el lápiz P es casi circular. La relación entre la distancia ST y la longitud del resto de la cuerda SP + PT se denomina «excentricidad» de la elipse; es necesariamente menor que la unidad, porque dos lados de un triángulo son juntos mayores que el tercero.
En el caso límite en el que la excentricidad se hace cero, la elipse se convierte en un círculo. Si la excentricidad es casi tan grande como la unidad, la elipse es muy alargada. Todas las diferentes formas de elipses se obtienen dejando que la excentricidad cambie de 0 a l, y representan todas las diferentes formas de órbita que un cuerpo pequeño puede describir alrededor de una masa gravitatoria pesada. Los puntos S, T se llaman focos de la elipse, y el gran cuerpo de atracción siempre ocupa uno u otro de los dos focos de la elipse. ↩︎Lo que en realidad observa es la «proyección» de la órbita en el cielo, pero es un teorema de geometría bien conocido que la proyección de una elipse es siempre una elipse. ↩︎
Por ejemplo, las Cefeidas cuya luz fluctúa en un período de 40 horas tienen aproximadamente una luminosidad 250 veces mayor que la del sol, por lo que son de 8 x 1029 candelas; un período de diez días indica una luminosidad 1600 veces mayor que la del sol, o una potencia de candela de 5,17 x 1030, y así sucesivamente. Si se observa que una estrella en un objeto astronómico distante fluctúa con un período de diez días, y la calidad de sus fluctuaciones muestra que es una variable cefeida, sabemos que su potencia de candela real debe ser 5,17 x 1030. Se observa que su brillo aparente es el de una estrella de, digamos, magnitud 16, lo que, despojado de tecnicismos, significa que recibimos tanta luz de ella como de una sola candela a una distancia de 570 millas [917 km]. La diferencia entre una candela y 5,17 x 1030 candelas corresponde a la diferencia entre 570 millas [917 km] y la distancia del objeto en cuestión, por lo que, dado que la luz cae como el inverso del cuadrado de la distancia, calculamos que la distancia del objeto debe ser
o unos 220.000 años luz. ↩︎