Autor: Sir James Jeans, M. A., D. Sc., Sc. D., LL. D., F. R. S.
[ p. 253 ] El proceso de tallar el universo que consideramos en el último capítulo termina normalmente con una estrella simple, aunque los accidentes especiales pueden tener otras consecuencias. Como resultado de los acercamientos con otras estrellas, una pequeña fracción del número total de estrellas, quizás alrededor de una estrella en 100.000 (p. 341 más abajo), puede estar acompañada por un séquito de planetas. Otra fracción, aún pequeña, aunque mucho mayor que la anterior, parece haberse disgregado como resultado de una rotación excesiva, y formado sistemas binarios o tal vez múltiples. Pero el destino de la mayoría de las estrellas es seguir su camino en solitario por el espacio, sin romperse por sí mismas ni ser rotas por otras estrellas. El único contacto que tales estrellas tienen con el universo exterior es que incesantemente arrojan radiación al espacio. Este flujo de radiación es casi en su totalidad un proceso unidireccional, cualquier radiación que una estrella pueda recibir de otras estrellas es bastante inapreciable en comparación con la cantidad que está emitiendo. La radiación va acompañada de una pérdida de peso, y esto nuevamente es todo dar y no recibir, el peso de cualquier materia perdida que la estrella pueda arrastrar fuera del espacio, como el de cualquier radiación que reciba, es bastante inapreciable en comparación con el peso que pierde por radiación. Sin forzar indebidamente los hechos, el objeto normal en el cielo puede idealizarse como un cuerpo solitario, solo en un espacio infinito, que emite radiación continuamente y no recibe nada a cambio.
En el presente capítulo consideraremos la secuencia [ p. 254 ] de los cambios que se espera que experimente tal estrella durante el curso de su vida. Habiendo discutido ya los accidentes mecánicos a los que están sujetas las estrellas, a saber, la fisión por rotación y la ruptura por la acción de las mareas de una estrella que pasa, ahora pasamos a considerar la vida de una estrella normal que escapa a todos los accidentes hasta que finalmente se extingue a través de la mera vejez.
Será necesario en primer lugar describir los estados físicos de los diversos tipos de estrellas observadas en el cielo, y como preliminar debemos explicar cómo las observaciones del astrónomo se traducen en una forma que nos da información directa como a la condición de la estrella.
Temperatura superficial. En el Capítulo II (p. 140) vimos cómo cada color de luz o longitud de onda de radiación tiene una temperatura especial asociada con él, predominando la luz de este color cuando un cuerpo se calienta hasta la temperatura en cuestión. Por ejemplo, un cuerpo elevado a lo que llamamos calor rojo emite más luz roja que la luz de cualquier otro color, y así parece rojo a la vista.
Así, si una estrella parece roja, es legítimo inferir que su superficie está a la temperatura que describimos como calor rojo. Si otra estrella tiene el color del carbono de un arco de luz, podemos concluir que su superficie está aproximadamente a la misma temperatura que el arco. De esta forma podemos estimar las temperaturas de las superficies de las estrellas.
En la práctica, el procedimiento no es tan rudimentario como parecería implicar la descripción anterior. El astrónomo pasa la luz de una estrella a través de un espectroscopio, analizándola así en sus diferentes colores. Mediante un proceso de medición exacta, determina las [ p. 255 ] proporciones en las que se dan los diferentes colores de la luz. Esto muestra inmediatamente qué color de luz es más abundante en el espectro de la estrella. De esto o de la distribución general de colores, puede deducir la temperatura de la superficie de la estrella.
Ya hemos visto (p. 123) cómo Planck descubrió la ley según la cual la radiación emitida por un radiador lleno se distribuye entre los diferentes colores o longitudes de onda del espectro. Las cuatro curvas mostradas en la fig. 15 representan la distribución teórica de la radiación emitida por superficies a las cuatro temperaturas 3000, 4000, 5000 y 6000 grados respectivamente. Las diferentes longitudes de onda de la luz están representadas por puntos en el eje horizontal, [ p. 256 ] las longitudes de onda marcadas se miden en la unidad de una cienmillonésima parte de un centímetro, que generalmente se denomina Angstrom. La altura de la curva por encima de dicho punto representa la abundancia de radiación de la longitud de onda en cuestión.
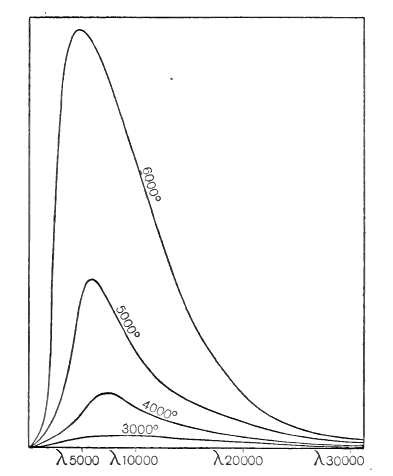
Los dos métodos para determinar la temperatura estelar se entenderán fácilmente con referencia a estas curvas. La curva de 6000 grados alcanza su altura máxima con una longitud de onda de 4800 Angstroms, de modo que si la luz con una longitud de onda de 4800 Angstroms resulta ser la más abundante en el espectro de cualquier estrella, sabemos que la superficie de la estrella tiene una temperatura de 6000 grados. El segundo método consiste simplemente en examinar a cuál de las curvas teóricas mostradas en la fig. 15 la curva observada se puede ajustar más estrechamente.
Cualquiera de estos métodos indica que la temperatura de la superficie del sol es de unos 6000 grados absolutos, que es casi el doble de la temperatura de la parte más caliente del arco eléctrico. La cantidad total de luz y calor recibida en la tierra del sol muestra que la radiación del sol debe ser muy cercana, aunque no del todo, a la «radiación de temperatura total» (p. 123) de un cuerpo a esta temperatura. Esto también se muestra por la distribución de la radiación del sol entre los diversos colores de una manera que se ajusta muy de cerca a la curva teórica para un radiador completo a 6000 grados que se muestra en la fig. 15.
La temperatura superficial de una estrella también se puede estimar a partir de su tipo espectral. Muchas de las líneas del espectro estelar son emitidas por átomos a los que el calor de la atmósfera de la estrella ha arrancado uno o más electrones. Conocemos las temperaturas a las que los electrones en cuestión se desprenden por primera vez de sus átomos, por lo que podemos deducir la temperatura de la estrella.
[ p. 257 ] Las temperaturas que corresponden a los diferentes tipos de espectros estelares, como se muestra en la Lámina VIII (p. 51), son aproximadamente las siguientes:
| Tipo espectral | Temperatura |
|---|---|
| B | 23,000 |
| A | 11,000 |
| F | 7,400 |
| G | 6,000 |
| K | 5,100 |
| M | 3,400 |
Las últimas tres entradas de la tabla se refieren únicamente a estrellas normales que tienen diámetros comparables con los del sol. Encontraremos (p. 276) que existe una segunda clase de estrellas (gigantes), cuyos diámetros son enormemente mayores que los del sol. Estos tienen las temperaturas sustancialmente más bajas que se muestran a continuación:
| Tipo espectral | Temperatura |
|---|---|
| G | 5600 |
| K | 4200 |
| M | 3200 |
Al estudiar la estructura y el mecanismo estelar, nos preocupa menos el calor de la superficie de la estrella medido por su temperatura que la cantidad de radiación que emite por pulgada cuadrada.
Esto, por supuesto, depende de la temperatura; cuanto más caliente es una superficie, más radiación emite. Pero la temperatura no mide la cantidad de radiación emitida. Si duplicamos la temperatura de una superficie, ésta emite 16 veces, no el doble, de su cantidad anterior de radiación; la radiación de cada pulgada cuadrada de superficie varía como la cuarta potencia de la temperatura. [ p. 258 ] Como consecuencia, una estrella con una temperatura superficial de 3000 grados, o la mitad de la del sol, emite solo una dieciseisava parte de la radiación por pulgada cuadrada que el sol. [1]. La radiación de cada estrella es un compuesto de luz, calor y radiación ultravioleta, y las proporciones de éstas no son las mismas en diferentes estrellas; cuanto más fría esté la superficie de estrella, mayor será la fracción de su radiación que se emite como calor. Por lo tanto, la estrella a 3000 grados emitirá algo parecido a un dieciseisavo de la luz del sol por pulgada cuadrada, pero emitirá más de un dieciseisavo del calor del sol.
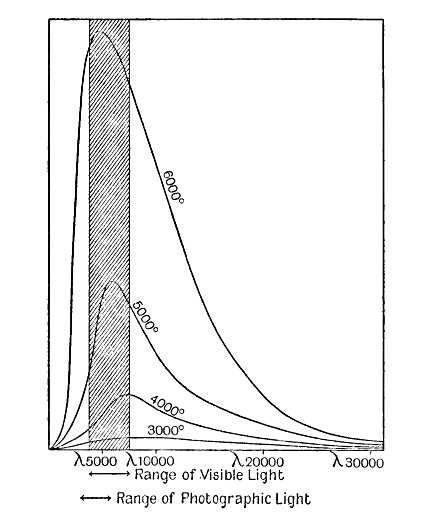
Esto demuestra que la emisión total de radiación de una estrella no puede estimarse únicamente a partir de su brillo visual; siempre se debe hacer una concesión sustancial para las radiaciones invisibles, tanto para el calor invisible en el extremo rojo del espectro como para la radiación ultravioleta invisible en el otro extremo. La importancia de estas correcciones se muestra en la fig. 16. Las cuatro curvas gruesas son idénticas a las ya dadas en la fig. 15, y muestra cómo la radiación de una estrella de temperatura superficial dada se distribuye en las diferentes longitudes de onda. Por supuesto, la radiación total emitida a cualquier temperatura está representada por el área total encerrada entre la curva correspondiente y el eje horizontal. El ojo sólo es sensible a la radiación de longitudes de onda comprendidas entre 3750 y 7500 Angstroms, de modo que de toda esta radiación sólo es visible la parte de la franja sombreada, representando todo el resto radiación invisible.
Vemos de inmediato que una buena proporción de la radiación emitida por una estrella a 6000 grados entra dentro del rango de visibilidad, pero solo una pequeña fracción de la emitida por una estrella a 3000 grados. Tomando las estrellas [ p. 259 ] en su conjunto, la luz de las estrellas constituye solo una pequeña parte de la radiación total de las estrellas.
Si nuestros ojos se hicieran repentinamente sensibles a todo tipo de radiación, y no sólo a la luz visual, la apariencia del cielo sufriría una extraña metamorfosis. Las estrellas rojas Betelgeux y Antares, que en la actualidad ocupan los lugares 12 y 16 en orden de brillo, destellarían como las dos estrellas más brillantes del cielo, mientras que Sirio, en la actualidad la más brillante de todas, se hundiría al tercer lugar. Una estrella en la muy poco distinguida constelación de Hércules sería vista como la sexta estrella más brillante del cielo. Es la estrella α Hércules, actualmente eclipsada por unas 250 estrellas. Como consecuencia de su temperatura extremadamente baja de 2650 grados, esta [ p. 160 ] emite su radiación casi en su totalidad en forma de calor invisible. Por ejemplo, emite 60 veces más calor que la estrella azul η Aurigae, cuya temperatura es de unos 20.000 grados, pero solo cuatro quintas partes de luz.
En todos los cálculos a los que se hace referencia en el presente libro se han hecho concesiones para la radiación invisible, aunque no se ha considerado necesario repetir esto continuamente.
Diámetros estelares. Es fácil medir el diámetro de un planeta, porque este aparece en el telescopio como un disco de tamaño finito. Pero las estrellas están demasiado alejadas para medir sus diámetros de la misma manera. Ninguna estrella parece más grande en el cielo que la cabeza de un alfiler mantenida a una distancia de seis millas, y ningún telescopio construido hasta ahora puede mostrar un objeto de este tamaño como un disco. Todas las estrellas, incluso las más cercanas y las más grandes, aparecen como meros puntos de luz[2], por lo que sus diámetros solo pueden medirse mediante métodos indirectos.
Cuando se conoce la distancia de una estrella, podemos saber su luminosidad a partir de su brillo aparente. A partir de esto, después de permitir la radiación invisible, podemos deducir el flujo total de energía de la estrella: tantos millones de millones de millones de millones de caballos de fuerza. También conocemos su efusión de energía por pulgada cuadrada de superficie, porque esto depende únicamente de la temperatura de su superficie, que deducimos directamente de la observación espectroscópica. Conociendo estos dos datos, es cuestión de simple división calcular el número de pulgadas cuadradas que forman la superficie de la estrella, y esto nos dice inmediatamente el diámetro de la estrella.
Los diámetros de estrellas excepcionalmente grandes pueden ser [ p. 261 ] medidos más directamente por un instrumento conocido como interferómetro. Cuando enfocamos un telescopio en una estrella, estrictamente hablando, no vemos solo un punto de luz, sino un punto de luz rodeado por un sistema bastante elaborado de anillos de luz y oscuridad alternados, llamado patrón de difracción. Podría pensarse que el tamaño de estos anillos nos diría el tamaño de la estrella, pero los dos no tienen nada que ver entre sí. Los anillos representan un mero defecto instrumental, dependiendo su tamaño únicamente del tamaño y disposición óptica del telescopio. Siguiendo un método sugerido por Fizeau en 1868, el profesor Michelson ha demostrado cómo incluso este defecto puede convertirse en fines útiles, y con su ayuda ha producido lo que es quizás el instrumento más ingenioso y sensacional al servicio de la astronomía moderna: el interferómetro. En efecto, este instrumento superpone dos patrones de difracción separados de la misma estrella y contrasta uno contra el otro de tal manera que revela el tamaño de la estrella que los produce. Los diámetros de algunas de las estrellas más grandes se han medido de esta manera, por lo que podemos decir que conocemos sus tamaños por observación directa. En todos los casos el diámetro medido directamente concuerda bastante bien, aunque no perfectamente, con el calculado indirectamente en la forma ya explicada. Las discrepancias, que no son serias, parecen resultar de que las estrellas rojas no sean «radiadores completos» exactos en el sentido explicado en la p. 123.
El método del interferómetro solo está disponible para las estrellas más grandes, pero en el otro extremo de la escala, la teoría de la relatividad ha venido al rescate. Einstein demostró que era una consecuencia necesaria de su teoría de la relatividad que el espectro de una estrella se desplazara hacia el extremo rojo en una cantidad [ p. 262 ] dependiendo tanto del peso como del diámetro de la estrella. Si, entonces, se conoce el peso de una estrella, el cambio espectral observado debería decirnos inmediatamente su diámetro. Este cambio espectral se ha observado recientemente en la luz recibida de la compañera de Sirio, y las mediciones de su cantidad conducen a un valor para el diámetro de la estrella que concuerda exactamente con el calculado a partir de su luminosidad. Así, en ambos extremos de la escala, tanto para las estrellas más grandes como para las más pequeñas, la observación directa confirma los valores calculados para los diámetros de las estrellas.
En consecuencia, podemos sentir plena confianza en los diámetros calculados de todas las estrellas, aun cuando éstos no puedan comprobarse mediante mediciones directas. De hecho, una discrepancia entre los diámetros reales y calculados solo podría surgir de una manera. Los diámetros se calculan asumiendo que las estrellas emiten toda su radiación de temperatura. Si las estrellas hubieran sido parcialmente transparentes como las nebulosas, o cuerpos sólidos como la luna, esta suposición habría sido falsa, y su falsedad se habría mostrado de inmediato por las discordancias entre los diámetros calculados y medidos de las estrellas. El hecho de que no aparezcan grandes discordancias sugiere que las estrellas emiten radiación de temperatura casi completa en todo el rango de tamaño, desde el más grande hasta el más pequeño.
¶ La variedad de estrellas
La observación muestra que las características físicas de las estrellas varían enormemente, de modo que es fácil, como pronto veremos, contar una historia sensacional contrastando los extremos, poniendo las más brillantes contra las más tenues, las más grandes contra las más pequeñas, y así sucesivamente. Esto daría, [ p. 263 ] sin embargo, una impresión muy injusta de los habitantes del cielo; sería como juzgar a una nación por los gigantes y los enanos, los hombres fuertes y los hombres que ayunan, vistos dentro de la tienda del showman.
Obtendremos una impresión más equilibrada del grado real de diversidad mostrado por las estrellas como un todo si consideramos los estados físicos de aquellas estrellas que están más cerca del sol. Al tomarlos precisamente en el orden en que aparecen, evitamos cualquier sospecha de salir de nuestro camino para presentar estrellas simplemente porque son extrañas o excepcionales. Se puede esperar que el pequeño grupo de estrellas obtenido de esta manera forme una buena muestra de las estrellas en el cielo, aunque, por supuesto, no será una muestra lo suficientemente grande como para incluir extremos. No necesitamos discutir el sol mismo en detalle porque figurará como nuestra estrella estándar, con referencia a la cual se hacen todas las comparaciones.
El sistema de α Centauri. Este sistema consta de tres estrellas constituyentes, que se cree que son nuestros tres vecinos más cercanos en el espacio.
El más brillante, α Centauri A, es muy parecido al sol. Es del mismo color y tipo espectral, pero pesa un 14 por ciento más y es alrededor de un 12 por ciento más luminoso. Al ser del mismo color que el sol, emite la misma cantidad de radiación por pulgada cuadrada. Así, su luminosidad 12 por ciento mayor muestra que debe tener una superficie 12 por ciento mayor, y por lo tanto un diámetro 6 por ciento mayor que el sol.
El segundo constituyente, α Centauri B, es considerablemente más rojo que el sol, su temperatura superficial es de sólo unos 4400 grados frente a los 6000 grados del sol más o menos. Tiene el 97 por ciento del peso del sol, pero solo alrededor de un tercio de su luminosidad. Sin embargo, como consecuencia de su baja temperatura, necesita un 50 por ciento, más [ p. 264 ] área que el sol para descargar un tercio de la radiación solar; esto hace que su diámetro sea un 22 por ciento mayor que el del sol. α Centauri A y α Centauri B juntos forman un binario visual, los dos componentes giran uno alrededor del otro en un período de 79 años.
Ninguno de estos dos constituyentes es muy diferente del sol, pero la tercera estrella del sistema, Próxima Centauri, es de un tipo completamente diferente. Es de color rojo, con una temperatura superficial de sólo unos 3000 grados. Es extremadamente tenue, emite solo una diezmilésima parte de la luz del sol y tiene solo una catorceava parte del diámetro del sol. Se desconoce su peso.
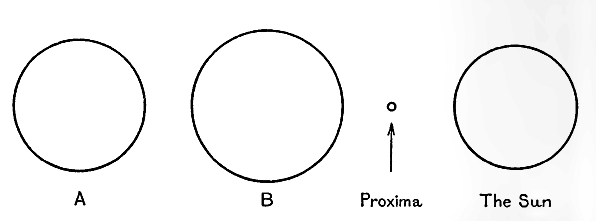
Los tamaños de las tres estrellas de este sistema, con el del sol como comparación, se muestran en la fig. 17.
Munich 15040. Se trata de una única estrella débil de la que se sabe poco. Su superficie es roja, con una temperatura probablemente un poco superior a los 2500 grados, y emite sólo de la luz del sol.
Wolf 359. Esta es la estrella más débil descubierta hasta ahora, pero más allá de esto se sabe muy poco sobre ella. Es de color rojo y emite solo alrededor de de la luz del sol.
[ p. 265 ] Lalande 21185. Otra estrella roja débil, que emite de la luz del sol.
El Sistema de Sirio. Consta de dos estrellas muy disímiles, existiendo cierta sospecha de que también pueda existir una tercera.
La estrella principal, Sirio A, que aparece como la estrella más brillante del cielo (la estrella Perro), es de color blanco y tiene una temperatura superficial de unos 11.000 grados. Como esto es casi el doble de la temperatura del sol, Sirius A emite casi 16 veces más radiación por pulgada cuadrada que el sol. Su luminosidad es unas 26 veces la del sol, y esto requiere que el diámetro de la estrella sea un 58 por ciento mayor que el del sol. Tiene casi cuatro veces el volumen del sol, pero sólo 2,45 veces su peso, por lo que la materia no está tan compacta en Sirio A como en el sol. Un metro cúbico promedio contiene 1,42 toneladas en el sol, pero solo 0,93 toneladas en Sirius A.
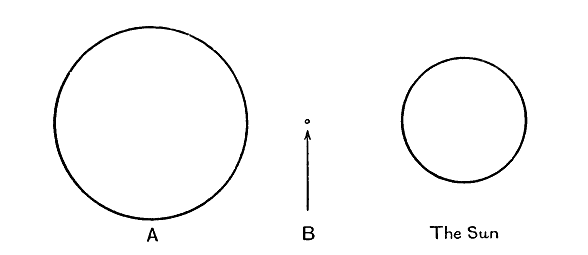
La tenue compañera Sirius B es una de las estrellas más interesantes del cielo. Es casi del mismo color y tipo espectral que Sirius A, pero emite solo una diezmilésima parte de esa cantidad de luz. Después de considerar la ligera diferencia en la temperatura de la superficie, encontramos [ p. 266 ] que su superficie es sólo un , y su diámetro del de Sirius A. Sin embargo, Sirius A pesa solo tres veces más que Sirius B, aunque tiene 125.000 veces su volumen. No es Sirius A sino Sirius B el que es notable; la densidad media de la materia en este último es unas 60.000 veces la del agua, y la pulgada cúbica media contiene casi una tonelada de materia. La Fig. 18 muestra los tamaños de los dos componentes de Sirius dibujados a la misma escala que la fig. 17.
B.D. 12° 4523 e Innes 11 h. 12 m., 57,2°. Dos estrellas, en cuanto a su estado físico nada se sabe, excepto que son muy débiles, emitiendo y la luz del sol respectivamente.
Córdoba 5 h. 343 y τ Ceti. Dos estrellas tenues, ambas de color rojizo, que emiten un y un tercio de la luz del sol respectivamente.
El Sistema de Procyon. Este es un sistema binario, similar en muchos aspectos a Sirio. La estrella principal, Procyon A, es del mismo tipo general que el sol, pero pesa un 24 por ciento más y emite un 5½ veces tanta [ p. 267 ] luz. Su temperatura superficial es de unos 7000 grados y su diámetro es 1,80 veces mayor que el del sol.
El compañero débil, Procyon B, es tan débil que no se sabe nada sobre su condición física excepto que emite solo de la luz del sol. Su peso es el 39 por ciento del peso del sol.
La Fig. 19 muestra los tamaños de los dos componentes de Procyon en la misma escala que antes.
A continuación, en orden, a medida que nos alejamos del sol, vienen ocho estrellas muy indistinguibles, cada una de las cuales es más roja y más débil que el sol, ninguna de ellas tiene una temperatura superficial superior a 5000 grados, y ninguna de ellas emite más de un cuarta parte de la luz del sol. Después de estos llegamos a
El Sistema de Kruger 60. Este es un sistema binario en el que ambos componentes son pequeños, rojos y tenues.

El componente más brillante, Kruger 60 A, tiene una temperatura superficial de 3200 grados y emite de la luz del sol. Su diámetro es un tercio, y su peso una cuarta parte del sol; de modo que su sustancia debe estar empaquetada unas 7 veces más cerca que la del sol. El componente más débil, Kruger 60 B, tiene una temperatura superficial similar pero emite solo de la luz solar. Su diámetro es un sexto y su peso un quinto de [ p. 268 ] la del sol; de modo que su sustancia debe estar empaquetada unas 40 veces más cerca que la del sol. El sistema se ilustra en la fig. 20.
Estrella de van Maaneri. Otra estrella muy tenue, que tiene una temperatura superficial alta de 7000 grados. Sin embargo, sólo emite de la luz del sol. En consecuencia, su diámetro es sólo alrededor de de la del sol, siendo la estrella más pequeña que la tierra. Se desconoce su peso, pero es muy probable que su sustancia esté aún más apretada que en Sirius B.
La discusión de esta muestra de estrellas sugiere que la mayoría de las estrellas en el espacio son más pequeñas, más frías y más débiles que el sol. Existen estrellas que son mucho más brillantes que el sol, pero son excepcionales, la estrella promedio en el cielo es un asunto pequeño y opaco en comparación con nuestro sol.
Con esta muestra de la población media del cielo que tenemos ante nosotros, podemos proceder a discutir las diversas características de las estrellas de forma sistemática, sin temor a mencionar extremos. Comencemos con sus pesos.
Pesos estelares. Las dos estrellas de menor peso conocido en todo el cielo son el componente débil de Kruger 60, que acabamos de discutir, y el componente más débil del sistema triple de ο2 Eridani, cada una de las cuales tiene una quinta parte del peso del sol. Pero las estrellas cuyos pesos se conocen son tan pocas que no puede haber justificación para suponer que se trata de los pesos más pequeños que se dan en todo el universo de las estrellas. Un estudio general de la situación, en líneas que se indicarán más adelante (p. 281), sugiere que puede haber muchas estrellas de peso aún menor, pero que muy [p . 269] pocas probablemente tengan pesos mucho más pequeños. Probablemente muy pocas estrellas pesan tan poco como una décima parte del peso del sol.
La gran mayoría de las estrellas tienen pesos intermedios entre este y diez veces el peso del sol. Las estrellas que pesan incluso tres veces más que el sol son raras, las que pesan diez veces más son muy raras, probablemente sólo una de cada 100.000 estrellas tiene diez veces el peso del sol. Indudablemente, se producen pesos aún mayores —ya hemos mencionado la estrella de Plaskett, cuyos dos constituyentes tienen más de 75 y 63 veces el peso del sol respectivamente, y el sistema cuádruple 27 Canis Majoris que, según todas las apariencias, pesa 940 veces más que el sol— pero tal los casos son muy, muy inusuales. Podemos decir que, como regla general, los pesos de las estrellas se encuentran dentro del rango de una décima a diez veces el peso del sol, y encontraremos que las estrellas difieren menos en sus pesos que en la mayoría de sus otras características físicas.
Luminosidad. Se muestra un rango mucho mayor, por ejemplo, en las luminosidades de las estrellas, en sus potencias de candela medidas en términos de la potencia de la candela del sol como unidad. La estrella más luminosa conocida es S Doradus, ya mencionada, con 300.000 veces la luminosidad del sol, mientras que la menos luminosa es Wolf 359 con sólo una quincuagésima milésima parte de la luminosidad del sol. La gama de luminosidades estelares, como de pesos estelares, se extiende casi por igual en los dos lados del sol, de modo que el sol es más bien una estrella mediana en cuanto a peso y luminosidad. Es media en el sentido de estar a mitad de camino entre los extremos, pero hemos visto que hay muchas más estrellas debajo que arriba.
[ p. 270 ] En comparación con el rango muy moderado de pesos estelares, el rango de luminosidad es enorme; S Doradus es 15.000.000.000 veces más luminoso que Wolf 359. Si S Doradus es un faro, Wolf 359 es algo menos que una luciérnaga, siendo el sol una vela ordinaria. Si el sol de repente comenzara a emitir tanta luz y calor como S Doradus, la temperatura de la tierra y todo lo que hay en ella subiría a unos 7000 grados, de modo que tanto nosotros como la tierra sólida desapareceríamos en una nube de vapor. Por otro lado, si la emisión de luz y calor del sol se hundiera repentinamente hasta la de Wolf 359, la gente en el ecuador de la tierra encontraría que su nuevo sol solo daría tanta luz y calor al mediodía como un fuego de carbón a milla de distancia; todos estaríamos congelados, mientras que la atmósfera terrestre nos rodearía en forma de un océano de aire líquido. Por lo que sabemos, no hay posibilidad de que el sol empiece a comportarse repentinamente como S Doradus, pero veremos más adelante que la posibilidad de que se comporte como Wolf 359 no es del todo un sueño visionario.
Superficie: temperatura y radiación. Se ha descubierto que Sirio tiene la temperatura superficial más alta de todas las estrellas cercanas al sol; es de unos 11.000 grados, o casi el doble de la del sol. Yendo más lejos, encontramos muchas estrellas con temperaturas superficiales mucho más altas. Por ejemplo, a la estrella de Plaskett se le atribuye una temperatura de 28.000 grados, aunque debe admitirse que un elemento sustancial de incertidumbre entra en todas las estimaciones de temperaturas estelares muy altas.
En el otro extremo, las temperaturas estelares que bajan hasta los 2500 grados son comparativamente comunes. Las temperaturas más bajas de todas están confinadas a las [ p. 271 ] estrellas variables de un tipo muy especial (variables de período largo) en las que la variación de la luz va acompañada de una variación en la temperatura de la superficie de la estrella y, de hecho, surge principalmente de ella. La temperatura de estas estrellas, cuando es la más baja, oscila hasta los 1650 grados, que está muy poco por encima de la temperatura de un fuego de carbón ordinario. En muchos de ellos, la temperatura varía en un amplio rango, pero nunca desciende tanto como para que la estrella se vuelva completamente invisible. Por lo tanto, hay un rango de temperatura por debajo de los 2500 grados que no se sabe que ocupe ninguna estrella, a excepción de las variables de período largo que solo ingresan a intervalos. Esto parecería sugerir que el número de estrellas absolutamente oscuras en el cielo es relativamente pequeño. Otras líneas de evidencia conducen a la misma conclusión. Si una estrella dejara de brillar, su atracción gravitatoria seguiría traicionando su existencia. Aunque no pudimos detectar una sola estrella oscura de esta manera, podríamos detectar una multitud. Si una gran proporción de estrellas fueran oscuras, probablemente sospecharíamos la existencia de estrellas oscuras por sus efectos sobre los movimientos del resto, de modo que las consideraciones gravitatorias generales excluyen la posibilidad de que haya un gran número de estrellas oscuras.
En lo que respecta a nuestro conocimiento actual, la temperatura de las superficies estelares oscila, en general, desde unos 30.000 grados hasta unos 2500, extendiéndose el límite inferior hasta unos 1650 para variables de periodo largo en sus temperaturas más bajas.
Aparte de las variables de período largo, este es solo un rango de 12 a 1, por lo que las temperaturas de las estrellas son más uniformes que sus luminosidades o sus pesos. Sin embargo, debemos recordar que la radiación de una estrella por pulgada cuadrada es mucho más fundamental que la temperatura de su superficie, y que un rango de 12 a 1 [ p. 272 ] en el último implica un rango de más de 20.000 a 1 en el primero. Si incluimos las variables de periodo largo, hay un rango de alrededor de 110.000 a 1 en la emisión de radiación por pulgada cuadrada.
En términos de caballos de fuerza, el sol emite energía a razón de 50 caballos de fuerza por pulgada cuadrada, una estrella con una temperatura superficial de 1650 grados emite solo 0,35 caballos de fuerza por pulgada cuadrada, mientras que la estrella de Plaskett, con una temperatura superficial de 28.000 grados, emite unos 28.000 caballos de fuerza por pulgada cuadrada. En lenguaje sencillo, cada centímetro cuadrado de esta última estrella vierte suficiente energía para mantener un transatlántico funcionando a toda velocidad, hora tras hora y siglo tras siglo. Y la energía emitida por centímetro cuadrado por las superficies de varias estrellas cubre toda la gama, desde la potencia de un transatlántico hasta la de un hombre en un bote de remos.
Tamaño. Las cuatro estrellas de mayor diámetro conocido son las siguientes:
| Estrella | Diámetro en términos de sol | Diámetro en millas |
|---|---|---|
| Antares | 450 | 390.000.000 |
| α Hércules | alrededor de 400 | 340.000.000 |
| ο Ceti (al máx.) | 300 | 260.000.000 |
| Betelgeux (promedio) | 250 | 210.000.000 |
Todos estos diámetros han sido medidos directamente por el interferómetro. En la escala utilizada en las figs. 17 a 20, en el que el sol es del tamaño de seis peniques, el círculo necesario para representar ο Ceti sería tan grande como el suelo de una habitación de buen tamaño, mientras que la segunda estrella del sistema (porque ο Ceti es binaria) sería del tamaño de un grano de arena. Podemos obtener una idea del inmenso tamaño de estas estrellas al notar que cada uno de sus diámetros es mayor que el diámetro de [ p. 273 ] la órbita de la tierra, de modo que si el sol se expandiera al tamaño de cualquiera de ellas nos encontraríamos dentro de ellas.
Estas estrellas deben ser extremadamente tenues. Antares, por ejemplo, ocupa 90.000.000 de veces más espacio que el sol, de modo que si su sustancia estuviera tan apretada, pesaría 90.000.000 de veces más que el sol. Sin embargo, en realidad, probablemente tiene sólo unas 40 o 50 veces el peso del sol, la diferencia entre este número y 90.000.000 se debe a la diferencia entre las densidades de Antares y el sol. En promedio, una tonelada de materia al sol ocupa considerablemente menos que una yarda cúbica [aprox. 1 m3·]; en Antares ocupa algo más de espacio que el interior de la Catedral de San Pablo. Sin embargo, un estudio detallado de los interiores estelares muestra que podemos atribuir muy poco significado a un promedio de este tipo. Es bastante probable que la materia en el centro de Antares esté tan compacta (pero no del todo) como la materia en el centro del sol (p. 291 a continuación). El enorme tamaño de Antares probablemente se deba principalmente a una atmósfera enormemente extendida de gas muy tenue, y no tiene mucho sentido encontrar un promedio entre esto y la materia compacta en el centro de la estrella.
Los objetos misteriosos conocidos como nebulosas planetarias, de los cuales se muestran ejemplos en la Lámina II (p. 28), quizás deberían considerarse como estrellas de diámetro aún mayor. En el centro de cada uno de ellos, el telescopio revela una estrella comparativamente débil con una temperatura superficial extremadamente alta. Rodeando esto está la nebulosidad de la que estos objetos derivan su nombre un tanto desafortunado. Con toda probabilidad, esta es simplemente una atmósfera de mayor extensión que la que rodea las cuatro estrellas de nuestra tabla. Van Maanen [ p. 274 ] estima que el diámetro de la nebulosidad de la Nebulosa del Anillo en Lyra (fig. 2 de la Lámina II) es 570 veces el de la órbita terrestre, o alrededor de 106.000.000.000 millas. Esta nebulosidad, sin embargo, difiere de la atmósfera de una estrella ordinaria en que es casi transparente; podemos ver a través de 106.000.000.000 millas de la Nebulosa del Anillo, pero solo podemos ver unas pocas decenas o cientos de millas en una estrella ordinaria.
En el otro extremo de tamaño, la estrella más pequeña conocida, la estrella de van Maanen (p. 268), es casi tan grande como la Tierra; más de un millón de estrellas de este tipo podrían estar empaquetadas dentro del sol y aún dejar espacio de sobra. Y, sin embargo, su peso es con toda probabilidad comparable, no con el de la tierra, sino con el del sol; supongo que puede tener alrededor de una quinta parte del peso del sol. Para empaquetar una quinta parte de la sustancia solar dentro de un globo del tamaño de la tierra, la tonelada promedio de materia debe empaquetarse en un espacio del tamaño de una cereza pequeña, aproximadamente diez toneladas por pulgada cúbica. La solidez de la tierra sugiere que sus átomos deben estar muy juntos, pero los átomos en la estrella de van Maanen deben estar 66.000 veces más juntos.
¿Cómo se hace? Como veremos en breve, sólo hay una respuesta posible. El átomo consiste principalmente en vacío: comparamos el átomo de carbono con seis avispas zumbando en la estación de Waterloo. Descompongamos el átomo en sus partes constituyentes, empaquetémoslas lo más cerca posible, y veremos la forma en que la materia está empaquetada en la estrella de van Maanen. Sin embargo, seis avispas que pueden deambular por toda la estación de Waterloo se pueden empaquetar dentro de una caja muy pequeña.
Gigantes y enanas. Hay una serie continua de estrellas entre los límites de peso que hemos [ p. 275 ] mencionado, y lo mismo ocurre con los límites de temperatura (y también de color) y de tamaño.
Dentro de estos límites especificados, puedo encontrarle una estrella de cualquier peso, color o tamaño que desee. Pero esto no quiere decir que usted pueda especificar el peso y el color y el tamaño de la estrella que desea, y que yo me encargaré de encontrarla para usted; si el peso es correcto, el color puede ser incorrecto, y así sucesivamente. Por ejemplo, si me pides una estrella roja te puedo encontrar una muy pesada o muy liviana, pero no sirve de nada que pidas una de peso intermedio. Hasta donde sabemos, las estrellas rojas de peso intermedio simplemente no existen. Lo mismo ocurre con el tamaño: no hay estrellas rojas de tamaño intermedio. Hertzsprung notó [ p. 276 ] en 1905 que las estrellas rojas se podían dividir claramente en dos clases distintas caracterizadas por su tamaño grande y pequeño: las llamó Gigantes y Enanas. Russell, al estudiar más a fondo la cuestión en 1913, confirmó las conclusiones anteriores de Hertzsprung y demostró que la división de las enanas gigantes se extendía a estrellas de otros colores además del rojo.
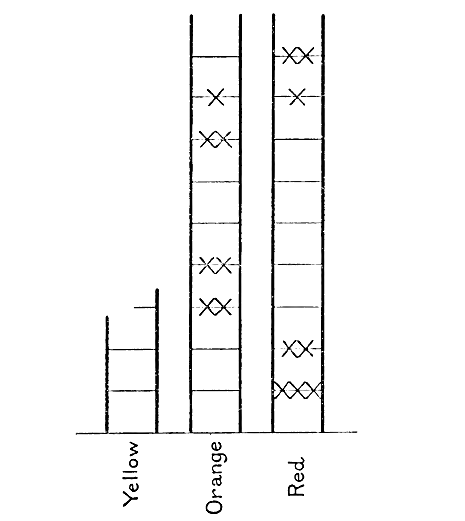
Imagina que tenemos una serie de escaleras de colores, una para cada color de estrella: rojo, naranja, etc. Toma todas las estrellas rojas y colócalas (en tu imaginación) en los diferentes peldaños de la escalera roja. No te limites a colocarlas al azar; colócalas en orden de luminosidad, colocando las de mayor luminosidad en primer lugar. Además, permite que varias estrellas estén en el mismo peldaño si sus luminosidades son aproximadamente iguales. Para definir el arreglo, deja que cada peldaño de la escalera represente una luminosidad 5 veces mayor que el peldaño inmediatamente debajo de él, de modo que cada peldaño tenga una luminosidad definida asociada con él[3].
Con este acuerdo, ahora estamos listos para proceder. Tomamos nuestras estrellas rojas y las colocamos en el peldaño apropiado de la escalera roja, y así sucesivamente para cada color. El resultado se muestra esquemáticamente en la fig. 21, estando las diferentes estrellas representadas por cruces.
Se encontrará que las estrellas rojas se encuentran a la derecha del diagrama, estando muy claramente marcada la división de Hertzsprung en gigantes y enanos. Las estrellas naranjas yacen como en la próxima escalera a la izquierda; como descubrió Russell, la división vuelve a aparecer, pero es menos marcada.
El diagrama de Russell. Hagamos diagramas de escalera de este tipo para cada color de estrella, y pongamos [ p. 277 ] una al lado de la otra en el orden correcto, para representar estrellas de todos los colores posibles. Obtenemos un diagrama del tipo que se muestra en la fig. 22. Este tipo de diagrama fue introducido por Russell en 1913 y ahora se conoce generalmente como diagrama de Russell.
Las letras en la parte superior del diagrama representan tipos espectrales de estrellas, porque proporcionan una clasificación de trabajo mejor y más exacta que los nombres de los colores. Los colores que corresponden aproximadamente a los distintos tipos espectrales se indican en la parte inferior del diagrama.
Solo se muestran unas pocas estrellas de muestra, pero se encuentra que todas las estrellas conocidas se concentran alrededor de las posiciones de estas pocas estrellas típicas. En términos generales, hay dos regiones distintas y desconectadas que están ocupadas por estrellas. Primero, y más importante, es una región con forma de y invertida: la línea central de esta región está marcada por una línea gruesa continua, siguiendo una determinación de su posición por parte de Redman. En segundo lugar, hay una región más pequeña cerca de la esquina inferior izquierda del diagrama. Las estrellas que ocupan esta región son muy débiles y tienen temperaturas superficiales mucho más altas que otras estrellas de luminosidad similar.
Ya hemos visto cómo se puede calcular el diámetro de una estrella a partir de su temperatura superficial y luminosidad. Esto equivale a decir que dos estrellas que ocupan la misma posición en el diagrama de Russell deben tener el mismo diámetro. Por lo tanto, hay un diámetro definido asociado con cada punto del diagrama, y podemos trazar los diámetros estelares en el diagrama, tal como podemos trazar las alturas sobre el nivel del mar en un mapa geográfico, mediante un sistema de «líneas de contorno». En el presente caso, las «curvas de nivel» resultan ser un sistema de curvas casi paralelas. Estos se encuentran [ p. 278 ] aproximadamente como lo muestran las líneas discontinuas en la fig. 22, todas las estrellas que se encuentran en cualquier línea que tiene el mismo diámetro.
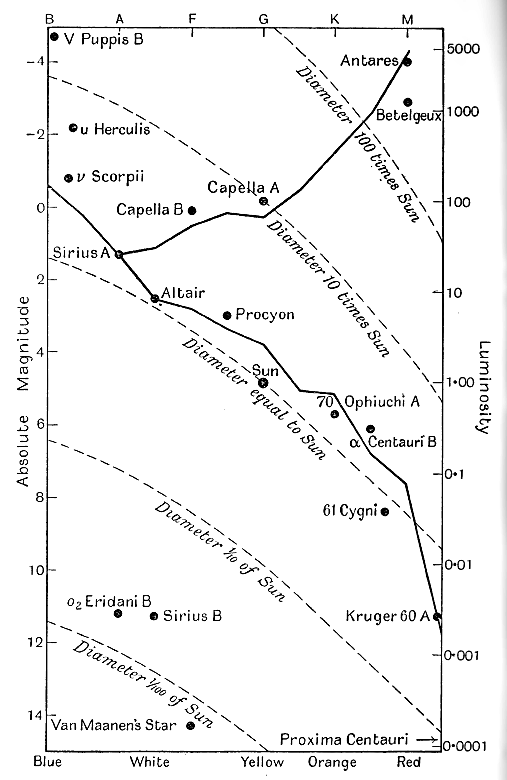
Este diagrama arroja mucha luz sobre la cuestión general de los diámetros estelares. Vemos de inmediato que las estrellas de los diámetros más grandes, 100 veces el diámetro del sol o más, deben ser necesariamente estrellas rojas de alta luminosidad. Y, de hecho, las estrellas de gran diámetro mostradas en la tabla de la p. 272 son todas rojas y tienen luminosidades muy altas; son gigantes rojas.
La mayoría de las estrellas del cielo se encuentran en el cinturón que atraviesa el diagrama de la fig. 22 de arriba a la izquierda a abajo a la derecha. Esto se conoce como la «secuencia principal». La posición de esta banda con referencia a las «líneas de contorno» de los diámetros muestra que las estrellas de la secuencia principal tienen diámetros moderados. La más brillante de todas puede tener veinte veces el diámetro del sol, mientras que la más débil puede tener sólo una vigésima parte del diámetro del sol, pero todas tienen diámetros que son al menos comparables con el del sol. La muestra de estrellas cercanas al sol, que ya hemos discutido, proporciona muchos ejemplos de estrellas de la secuencia principal; tenemos, en orden decreciente de luminosidad:
| Estrella | Luminosidad | Diámetro (en términos de sol) |
|---|---|---|
| Sirio A | 26,3 | 1,58 |
| Proción A | 5,5 | 1,80 |
| α Centauro A | 1,12 | 1,07 |
| sol | 1,00 | 1,00 |
| α Centauro B | 0,32 | 1,22 |
| τ Ceti | 0,32 | 0,95 |
| ε Indi | 0,15 | 0,82 |
| Kruger 60A | 0,0026 | 0,33 |
| Kruger 60B | 0,0007 | 0,17 |
| Wolf 359 | 0,00002 | 0,03 |
[ p. 280 ] Esta tabla muestra claramente cómo la luminosidad y el diámetro estelar disminuyen juntos a medida que avanzamos por la secuencia principal.
El grupo restante de estrellas en la fig. 22, las que se encuentran en la esquina inferior izquierda, generalmente se conocen como «enanas blancas». Su posición en el diagrama muestra que sus diámetros deben ser excesivamente pequeños. La vecindad del sol proporciona tres ejemplos de esta clase de estrella, como se muestra en la siguiente tabla:
| Estrella | Luminosidad | Diámetro (en términos de sol) |
|---|---|---|
| Sirio B | 0,0026 | 0,03 |
| ο2 Eridani B | 0,0031 | 0,018 |
| la estrella de van Maanen | 0,00016 | 0,009 |
Además de estos, el débil compañero de ο Ceti es ciertamente una enana blanca, mientras que Procyon B puede serlo. Estos son los únicos ejemplos conocidos de enanas blancas, pero la extrema debilidad de estas estrellas las hace muy difíciles de detectar, por lo que es muy probable que sean objetos bastante frecuentes en el espacio.
En la tabla de la p. 279, se pretendía que las estrellas de la secuencia principal estuvieran dispuestas en el orden de luminosidad, pero esto también es el orden de los pesos. Se desconocen los pesos de tres de las estrellas; las del resto son las siguientes:
| Estrella | Luminosidad | Peso (en términos de sol) |
|---|---|---|
| Sirio A | 26,3 | 2,45 |
| Proción A | 5,5 | 1,24 |
| α Centauro A | 1,12 | 1,14 |
| sol | 1,00 | 1,00 |
| α Centauro B | 0,32 | 0,97 |
| Kruger 60A | 0,0026 | 0,25 |
| Kruger 60B | 0,0007 | 0,20 |
[ p. 281 ] Al igual que las luminosidades, los pesos disminuyen constantemente a medida que avanzamos por la secuencia principal, aunque, como ya se señaló, el peso disminuye mucho menos rápidamente que la luminosidad.
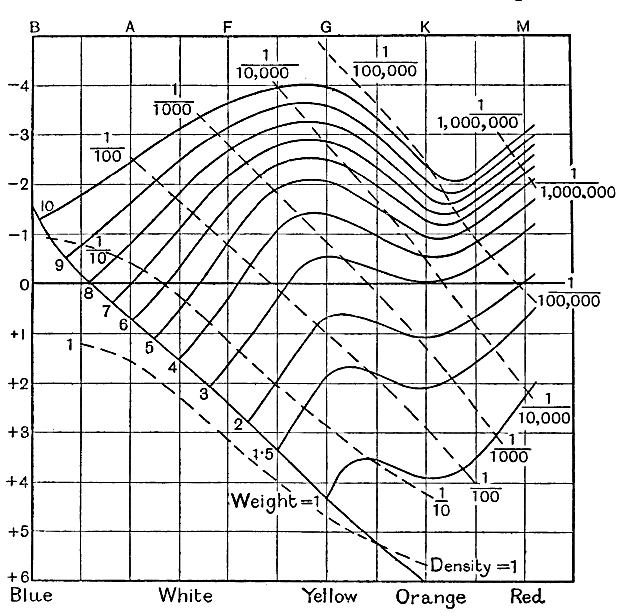
Las únicas estrellas cuyos pesos pueden medirse directamente son las componentes de los sistemas binarios, y éstas son relativamente pocas en número. Seares encontró, sin embargo, que los pesos de los sistemas binarios se ajustaban a la ley de equipartición de energía ya explicada en el Capítulo III, de modo que es muy probable que otras estrellas que no son binarias también se ajusten, ya que es difícil imaginar alguna razón por la cual los sistemas binarios deberían alcanzar un estado de equipartición antes que otras estrellas. Se recordará que este estado está definido por una ley puramente estadística que relaciona los pesos y las velocidades de movimiento de las estrellas, de modo que el hecho de que un sistema de estrellas haya alcanzado este estado no puede dar información sobre el peso de una estrella individual cuya velocidad es conocida, pero hace posible determinar el peso medio de cualquier grupo de estrellas en función de sus velocidades medias de movimiento. De esta forma, Seares ha determinado los pesos medios de las estrellas de diferentes luminosidades y tipos espectrales asignados; en otras palabras, los pesos medios de las estrellas representadas en los distintos puntos del diagrama de la fig. 22. Los resultados que obtuvo se muestran por las gruesas líneas curvas en la fig. 23. La disposición de estas curvas confirma la inferencia que hemos extraído de unas pocas estrellas seleccionadas; el peso de las estrellas de la secuencia principal disminuye constantemente a medida que avanzamos en la secuencia de alta a baja luminosidad.
Estas líneas curvas especifican el peso medio de las estrellas representadas en cada punto del diagrama de Russell, y los diámetros ya se conocen por la fig. 22. A partir de estos dos datos, la densidad media de la [ p. 282 ] estrella, por supuesto, se puede calcular. Las densidades medias calculadas por Seares se muestran mediante líneas discontinuas en la fig. 23.
Esto completa nuestra colección de material de observación. Pasamos ahora al problema mucho más difícil de discutir qué significa todo esto. Aquí dejamos el terreno firme de los hechos comprobados para entrar en las ciénagas sombrías de las conjeturas, las hipótesis y las especulaciones. Las cuestiones que discutiremos son algunas de las más interesantes de toda la astronomía, a las que debe [ p. 283 ] debe admitirse que la ciencia hasta ahora ha obtenido respuestas lamentablemente polvorientas. El lector apasionado por las certezas puede preferir leer algo más que el resto del presente capítulo.
¶ La condición física de las estrellas
La recopilación anterior de datos de observación ha proporcionado pruebas abundantes de que las estrellas con ciertas especificaciones no existen en absoluto. Para decir lo mismo de otra manera, hay ciertas regiones en el diagrama de Russell que están totalmente desocupadas por estrellas.
Para tomar el ejemplo más conspicuo de todos, no hay estrellas en absoluto a la izquierda de la secuencia principal en el diagrama de Russell (fig. 22), hasta que llegamos al grupo bastante aislado de enanas blancas. ¿Por qué no hay estrellas en condiciones intermedias? ¿Por qué, para hacer aún más preciso el ejemplo, no existe ninguna estrella del mismo color que Sirio pero con sólo una décima parte de su luminosidad? ¿Por qué tenemos que descender a la enana blanca de ο2 Eridani B, con una luminosidad de solo una diezmilésima parte de la de Sirio, antes de que podamos encontrar una estrella del mismo color que Sirio?
Una hipótesis que se le ocurre naturalmente a la mente es que las estrellas de la secuencia principal y las enanas blancas pueden formar grupos distintos porque son de edades completamente diferentes: pueden representar creaciones distintas. A medida que las estrellas envejecen, disminuyen en peso y luminosidad, por lo que es natural interpretar los pesos pequeños y la luminosidad extremadamente baja de las enanas blancas como evidencia de una edad mucho mayor que la edad de las estrellas normales de la secuencia principal. Sin embargo, esta hipótesis no parece ser sostenible.
Con la única excepción de la estrella de van Maanen, todas las estrellas que se sabe o se sospecha que son [ p. 284 ] una enana blanca forman un componente de un sistema binario, y en todos los casos su compañera es una estrella de secuencia principal o (en el caso de ο Ceti) una gigante roja. Ya hemos visto lo raro que es que dos estrellas se acerquen en el espacio. Debe ser un evento casi inconcebiblemente raro que dos estrellas, originalmente moviéndose como cuerpos independientes, se encuentren en sus vagabundeos aleatorios, que la grande «capture» a la pequeña, y de ahí en adelante viajen juntas a través del espacio. Porque se puede demostrar que, para que tal evento ocurra, se necesita algo más que un acercamiento próximo; un acercamiento próximo debe tener lugar en presencia de una tercera estrella, de modo que no menos de tres estrellas deben tener la oportunidad de acercarse una a la otra simultáneamente en sus vagabundeos a través de los vastos vacíos del espacio. Es casi inconcebible que esto suceda en un solo caso, pero está forzando demasiado las probabilidades para suponer que ha sucedido en el caso de todas las enanas blancas conocidas menos una. Por lo tanto, debemos suponer que las enanas blancas y sus compañeras más normales han estado juntas desde su nacimiento, por lo que nacieron al mismo tiempo de la misma nebulosa.
La diferencia entre las enanas blancas y las estrellas de secuencia principal no puede ser, entonces, una mera diferencia de edad, y parece que debe haber alguna razón física que milita en contra de la existencia de estrellas en condiciones intermedias. Tomando una visión más general de la cuestión, nos vemos obligados a investigar si la ausencia de estrellas construidas con ciertas especificaciones puede atribuirse a que tales estrellas necesitan propiedades físicas que la naturaleza no puede proporcionar. Esto lleva directamente a la cuestión general de la estructura y el mecanismo de las estrellas. [ p. 285 ]
¶ La constitución interna de las estrellas
La mayoría de las investigaciones sobre la estructura de las estrellas se han realizado bajo la suposición de que sus interiores son completamente gaseosos. Sin aceptar esta suposición como verdad final, podemos adoptarla por el momento, por la razón puramente oportunista de que proporciona la línea de enfoque más conveniente para un problema excesivamente difícil.
Un teorema matemático, generalmente conocido como el teorema de Poincaré, demuestra ser de gran utilidad para discutir el estado interno de una estrella gaseosa. Hemos visto cómo Helmholtz pensó que la energía de la radiación del sol podría provenir de la contracción del sol, cada capa cayendo sobre la siguiente capa interna a medida que esta última se encogía, y transformando la energía liberada por su caída en calor y luz. Es fácil estimar cuánta energía sería liberada por una contracción de este tipo. Por ejemplo, Lord Kelvin calculó que la contracción del sol, al encogerse desde un tamaño infinito hasta su diámetro actual de 865.000 millas, liberaría tanta energía como la que el sol irradia ahora en 50 millones de años. En términos de ergs, la contracción del sol liberaría 6 x 1048 ergs de energía.
El teorema de Poincaré establece que la energía total de movimiento de todas las moléculas en cualquier estrella gaseosa es exactamente igual a la mitad de la energía total que la estrella habría liberado al reducirse a su tamaño actual. El teorema es verdadero independientemente de si la estrella se ha encogido tanto o no: nada está involucrado excepto el estado actual de la estrella.
Una consecuencia interesante es que cuanto más se encoge una estrella gaseosa, más caliente se vuelve; si una estrella [<pequeña>p. 286] se encoge a la mitad de su tamaño actual, la energía total liberada por su contracción del tamaño infinito se duplica, de modo que la energía total de movimiento de sus moléculas se duplica, y por lo tanto su temperatura media se duplica. Este es un caso especial de lo que generalmente se conoce como ley de Lane.
Prosigamos con nuestro cálculo para el caso especial del sol. El teorema de Poincaré nos dice que, si el sol es gaseoso, la energía total de movimiento de todas sus moléculas es de 3 x 1048 ergios. Lo siguiente que queremos saber es cuántas moléculas hay en el sol. El peso del sol es de 2 x 1033 gramos, pero ¿cuántas moléculas hay en un gramo? La respuesta, por supuesto, depende del tipo de molécula en cuestión; hay 3 x 1023 moléculas en un gramo de hidrógeno, 2 x 1022 en un gramo de aire y sólo 2,5 x 1021 en un gramo de uranio.
Si suponemos que el sol está hecho de aire, debe constar de 4 x 1055 moléculas, de modo que la energía media de movimiento de cada molécula debe ser de 7,5 x 10-8 ergs, y esto representa una temperatura media, para el interior del sol, de 375 millones de grados. En 1907, Emden, mediante un cálculo diferente, descubrió que si el sol estuviera hecho de aire, la temperatura en su centro sería de 455 millones de grados. Más allá de los detalles, está claro que la temperatura interior de un sol hecho de aire sería de cientos de millones de grados.
Hasta ahora, todos los estudios de los interiores estelares se habían realizado sobre la suposición de que las estrellas estaban formadas por átomos completos o incluso por moléculas. En 1917 hice un cálculo sencillo, del tipo ya explicado en la p. 141, y descubrí que los cuantos de radiación que vuelan a tales temperaturas serían lo suficientemente energéticos no solo para romper las moléculas de aire en átomos, sino también [ p. 287 ] también para quitar todos, o casi todos, los electrones de los átomos. A tales temperaturas, cada molécula de aire se rompería en sus núcleos y electrones constituyentes con la misma seguridad que, en un día caluroso, un trozo de hielo se rompe en sus moléculas constituyentes. Las fuerzas eléctricas que, en un entorno más tranquilo, unirían los electrones y los núcleos, primero en átomos y luego en moléculas completas, se encuentran impotentes contra la lluvia incesante de proyectiles que se mueven rápidamente y los golpes demoledores de cuantos de alta energía; sería como tratar de construir un castillo de naipes en medio de un huracán. Un sol formado por moléculas de aire resulta ser una inconsistencia, una contradicción; nuestra hipótesis se ha derrotado a sí misma, y debemos empezar de nuevo desde el principio.
Podemos comenzar donde queramos, pero la conclusión a la que finalmente debemos llegar es que, sin importar de qué tipo de moléculas esté compuesto el sol, el calor en el centro del sol las descompondrá, ya sea por completo o casi, en sus núcleos constituyentes y electrones. Lo mismo es cierto para todas las demás estrellas, y esto introduce una simplificación extrema en el problema de la constitución interior de las estrellas. No podemos decir cuántas moléculas completas hay en un gramo sin conocer la naturaleza de las moléculas, pero una vez que estas moléculas se descomponen en sus partes constituyentes, y conocemos de inmediato el número total de partes constituyentes, núcleos y electrones, que ir a hacer un gramo. Porque los pesos atómicos de todos los elementos excepto el hidrógeno son casi el doble de sus números atómicos (p. 110). Por lo tanto, como señaló Eddington por primera vez, el número total de núcleos y protones en un átomo completamente fragmentado de cualquier sustancia, excepto el hidrógeno, debe ser igual a aproximadamente la mitad del peso atómico [ p. 288 ] del átomo. Probablemente podemos descartar la posibilidad de que una estrella consista en gran medida en hidrógeno. Si es así, el número de partes constituyentes en un gramo de materia estelar completamente fragmentada debe ser de aproximadamente 3 x 10^23, independientemente del tipo de molécula de la que se originen estas partes. Y cuando conocemos el número total de tales partes en cualquier estrella, se vuelve fácil calcular la temperatura del interior de la estrella, ya sea a partir del teorema de Poincaré que acabamos de mencionar o de otra manera. La temperatura será la misma que si la estrella estuviera hecha de moléculas enteras de hidrógeno.
Emden calculó en 1907 que la temperatura central de un sol de este tipo sería de unos 31.500.000 grados. Cálculos posteriores y más refinados de Eddington condujeron a una temperatura casi idéntica, pero algunos cálculos propios aún posteriores dan una cifra sustancialmente más alta de 55.000.000 grados. No hay necesidad por el momento de discutir cuál de estas cifras es la más cercana a la verdad. Su diversidad indicará qué tipo de grado de incertidumbre acompaña a todos los cálculos de este tipo.
Es fácil ver la necesidad física de esta alta temperatura. El calor que se aleja de la superficie del sol debe haber sido traído primero desde su interior. El calor solo fluye de un lugar más caliente a un lugar más frío, y un flujo vigoroso de calor es evidencia de un gradiente de temperatura pronunciado. La temperatura debe aumentar bruscamente a medida que pasamos de la superficie del sol hacia su centro, y este aumento, continuado a lo largo de las 433.000 millas hasta el centro, debe dar como resultado que se alcance allí una temperatura muy alta.
La temperatura central calculada de 30 a 60 millones de grados hasta ahora trasciende nuestra experiencia de que [ p. 289 ] es difícil darse cuenta de lo que significa. Mantengamos, en la imaginación, un milímetro cúbico de materia ordinaria —un trozo del tamaño de la cabeza de un alfiler ordinario— a una temperatura de 50.000.000 de grados, la temperatura aproximada en el centro del sol. Por increíble que parezca, simplemente para mantener esta cabeza de alfiler de materia a tal temperatura, es decir, para reponer la energía que pierde por la radiación de sus seis caras, se necesitará toda la energía generada por un motor de tres mil millones de millones de caballos; la cabeza de alfiler de materia emitiría suficiente calor para matar a cualquiera que se aventurara a menos de mil millas de ella.
Por alta que sea esta temperatura, los cálculos muestran que no sería suficiente para romper completamente las moléculas estelares. Despojaría a los átomos de todos sus electrones hasta los anillos K (p. 134), pero estos permanecerían intactos. Necesita temperaturas aún más altas que las que ahora estamos considerando para despojar a los electrones del anillo K del núcleo de un átomo. Este resultado es cierto para todo el rango, desde alrededor de 30 a 60 millones de grados, dentro del cual es probable que se encuentre la temperatura del centro del sol, y es cierto casi independientemente del peso atómico o número atómico de los átomos de los cuales suponemos que el sol está construido.
Por lo tanto, si el sol es totalmente gaseoso, sus partes centrales deben consistir en una colección de átomos reducidos a sus anillos K, pero no más allá, volando independientemente como las moléculas de un gas, y con ellas, también volando como las moléculas de un gas, todos los electrones despojados que originalmente formaron el anillo L, el anillo M, etc., de los átomos, estando todo a una temperatura de entre 30 y 60 millones de grados. A medida que avanzamos hacia la superficie del sol, llegamos a temperaturas más bajas, en las que los átomos [ p. 290 ] están menos fragmentados. Finalmente, cerca de la superficie del sol, podemos encontrar átomos que están completamente formados excepto quizás por uno o dos de sus electrones más externos. En las superficies de las estrellas más frías de todas, encontramos incluso moléculas completas, como, por ejemplo, las moléculas de óxido de titanio e hidruro de magnesio, que se muestran en los espectros de las estrellas rojas.
Cuando se investiga de la misma manera la constitución interna de otras estrellas, se encuentra que todas las estrellas de la secuencia principal tienen aproximadamente las mismas temperaturas centrales que el sol. Además, esta no es la única propiedad que tienen en común. La Fig. 23, que muestra los cálculos de Seares de las densidades estelares medias, muestra que las densidades medias de las estrellas de la secuencia principal son todas aproximadamente iguales, excepto por desviaciones comparativamente pequeñas en los dos extremos.
La densidad media del sol es 1,4, lo que significa que el metro cúbico promedio en el sol contiene 1,4 toneladas de materia. En el centro del sol, la densidad es unas 100 veces mayor, de modo que un metro cúbico contiene unas 140 toneladas de materia. A modo de comparación, un metro cúbico de plomo contiene solo unas 11 toneladas. Si todas las estrellas estuvieran construidas sobre el mismo modelo que el sol, dos estrellas cualesquiera que tuvieran la misma densidad media también tendrían densidades iguales en sus centros. Pero en las estrellas que tienen varias veces el peso del sol, entra en juego un nuevo factor, a saber, la presión de la radiación, la presión que ejerce la radiación en virtud del peso que lleva consigo. En la mayoría de las estrellas esta presión es insignificante en comparación con la presión producida por el impacto de los átomos materiales y los electrones, pero en estrellas muy masivas es lo suficientemente grande como para influir en la estructura de la estrella. Es por esto que [ p. 291 ] las estrellas muy masivas cuyos diámetros están tabulados en la p. 272 deben su tamaño anormalmente grande. Es una consecuencia general de los efectos perturbadores de la presión de radiación que el peso de una estrella muy masiva esté mucho más concentrado en sus regiones centrales que el de una estrella más ligera, de modo que si una estrella ligera y una masiva tienen el mismo promedio densidad, esta última tendrá, con mucho, la mayor densidad en su centro. Cuando se tiene en cuenta este factor perturbador, se encuentra que todas las estrellas en la parte superior de la secuencia principal tienen aproximadamente las mismas densidades en sus regiones centrales, una densidad casi igual a la del centro del sol. que podemos estimar en 140 toneladas por metro cúbico. Y ya hemos visto que las regiones centrales de estas estrellas tienen también aproximadamente las mismas temperaturas que el centro del sol, de donde se sigue que sus condiciones físicas son todas sustancialmente las mismas. Así, los átomos de las regiones centrales de todas estas estrellas deben descomponerse en la misma medida que los átomos de las regiones centrales del sol. Los anillos K de electrones sobreviven intactos, pero los anillos exteriores se transforman en una lluvia de electrones que vuelan como moléculas independientes.
Con suficiente precisión para nuestro presente propósito, se puede suponer que todas las estrellas de la secuencia principal, excepto quizás las del extremo inferior, se encuentran en la misma condición física. Debido a esta propiedad, la secuencia principal forma una base admirable a partir de la cual realizar un estudio del diagrama de Russell con respecto a las condiciones físicas de los interiores estelares.
La Fig. 22 muestra que una estrella a la derecha de la secuencia principal tiene un diámetro mayor que una estrella de la secuencia principal del mismo peso. En consecuencia, la energía [ p. 292 ] que emitiría al reducirse a su diámetro actual es menor y, por lo tanto, su energía molecular de movimiento es menor (según el teorema de Poincaré). De ello se deduce que sus temperaturas internas son más bajas y sus átomos se rompen menos completamente. Se encuentra que las gigantes rojas como Antares solo tienen temperaturas centrales de uno a cinco millones de grados, y sus átomos probablemente retienen intactos no solo sus anillos K de electrones, sino también sus anillos L y al menos parte de sus anillos M.
A la izquierda de la secuencia principal llegamos a una región en la que las estrellas, si es que existieron, se habrían encogido aún más y, por lo tanto, tendrían temperaturas más altas y átomos más fragmentados. En realidad, no se encuentran estrellas hasta que llegamos a las enanas blancas. Los cálculos muestran que las temperaturas centrales de estas deben ser de muchos cientos de millones de grados por lo menos, y que sus átomos deben estar despojados de electrones hasta el núcleo. Excepto por un pequeño número de átomos que pueden haber escapado a este destino general, la materia estelar debe consistir en núcleos absolutamente desnudos y en electrones libres, todos volando independientemente a través de la estrella. Las altas densidades de estas estrellas proporcionan una prueba convincente de la precisión de este resultado. La densidad media de Sirius B es ciertamente superior a 50.000, mientras que la estrella de van Maanen es probablemente más de 300.000. No hay forma de empaquetar la materia de forma tan estrecha como ésta, excepto despojando a los átomos de electrones hasta el núcleo desnudo.
La impresión general más clara que podemos formarnos del diagrama de Russell en términos de condición física se obtiene probablemente de la siguiente manera:
Primero pensamos en dos bandas separadas de estrellas, una, el grupo de enanas blancas, formado por estrellas en las que todos [ p. 293 ] los electrones son arrancados de los átomos; y la otra, la secuencia principal, formada por estrellas en las que los átomos están todavía rodeados por sus anillos K de electrones, mientras que los anillos exteriores han sido arrancados. Aproximadamente a partir de la mitad de la secuencia principal está la rama espuela que conduce a las gigantes rojas, como se muestra en la fig. 22. A medida que avanzamos, las temperaturas internas de las estrellas disminuyen, de modo que los átomos estelares se rompen menos que en las estrellas de la secuencia principal. En las gigantes rojas en el extremo, incluso los electrones del anillo M aún pueden permanecer.
¶ Hipótesis de Russell
Se han sugerido dos explicaciones completamente diferentes de esta distribución de estrellas. En 1925, Russell presentó una teoría que se centraba principalmente en el hecho de que las temperaturas en los centros de las estrellas de la secuencia principal son prácticamente iguales. Simplifiquemos la situación por un momento imaginando que es un hecho comprobado que las temperaturas en los centros de todas las estrellas son exactamente las mismas, digamos 32.000.000 grados. Si esto fuera un hecho seguro, sería natural conjeturar que las estrellas tenían algún tipo de mecanismo de control mediante el cual ajustaban continuamente su temperatura central a esta cifra exacta, de modo que si alguna vez la temperatura descendía por debajo de los 32.000.000 grados, el mecanismo entraría en juego y elevaría la temperatura precisamente a esta cantidad, mientras que si aumentara por encima de esta cifra, el mecanismo entraría en juego y lo deprimiría. Tales mecanismos de control son, por supuesto, comunes en la práctica de la ingeniería; están por ejemplo las válvulas de seguridad que mantienen la presión en una caldera siempre uniforme, los [ p. 294 ] gobernadores centrífugos de Watts que mantiene un motor funcionando siempre a la misma velocidad, y el termostato que mantiene constante la temperatura de una habitación.
Ya se conoce un mecanismo para elevar la temperatura en el centro de una estrella. Si una estrella no está generando energía alguna en su interior, ya sea por aniquilación de la materia o de otro modo, su emisión de radiación hace que se encoja, y esto, como hemos visto (p. 285), hace que aumente su temperatura. Por lo tanto, es fácil mantener la temperatura central de una estrella hasta los 32.000.000 grados disponiendo que no se genere energía mientras la temperatura en el centro esté por debajo de los 32.000.000 grados, y esta es la hipótesis principal en la que se basa la teoría de Russell. Supone que la materia no genera energía alguna a temperaturas por debajo de los 32.000.000 grados, pero que, tan pronto como se alcanza esta temperatura, la materia comienza a aniquilarse en cantidad suficiente para proporcionar la radiación de una estrella.
El problema con la teoría es que parece imposible regular la temperatura desde el otro extremo. Una estrella cuya temperatura central esté por debajo de los 32.000.000 grados debe estar contrayéndose sin generar calor. La contracción no se detendrá en seco en el momento en que se alcance la temperatura crítica; su impulso lo llevará hasta que la temperatura central supere sustancialmente los 32.000.000 grados. Tan pronto como la temperatura exceda seriamente los 32.000.000 grados en el centro, la de una parte sustancial de la estrella será de 32.000.000 grados o más. La aniquilación de toda esta materia debe producir una profusión de calor que elevaría aún más la temperatura de la estrella, resultando en más y más aniquilación de materia, hasta que finalmente toda la estrella desapareciera [ p. 295< /sup>] en un destello de radiación. De hecho, la teoría de Russell supone que la materia a 32.000.000 de grados está en una condición similar a la de la pólvora en su punto de inflamación. El análisis matemático muestra entonces que una estrella cuyo centro está a una temperatura de 32.000.000 grados estaría en el estado de un barril de pólvora con una chispa en su centro, y bueno, «ohne hast, ohne rast» [del alemán, «sin prisa, sin descanso»] difícilmente describe el curso subsiguiente de eventos.
Eddington ha sugerido que la estabilidad de las estrellas podría salvarse imaginando un lapso de tiempo entre el instante en que la materia alcanzó la temperatura crítica necesaria para la aniquilación y el instante en que ocurrió esta aniquilación. Todavía no se ha probado que el remedio propuesto pueda hacerse efectivo, pero aun si pudiera, subsisten otras dificultades. Como la estrella normal habita en la secuencia principal, Russell supuso que era una propiedad de la materia normal aniquilarse a una temperatura de unos 32.000.000 grados, la temperatura central supuestamente uniforme de todas las estrellas de la secuencia principal. Entonces se hizo necesario introducir más suposiciones especiales para explicar la luminosidad de las enanas blancas y de las estrellas en la línea en espuela de las gigantes rojas, cuyos centros están a temperaturas muy diferentes de 32.000.000 grados. En consecuencia, supuso que tales estrellas contenían otros tipos de materia que se disolvían en radiación a temperaturas que eran, respectivamente, superiores e inferiores a 32.000.000 de grados. Incluso si pudiera superarse la dificultad de la estabilidad, esta última serie de supuestos me parece tan artificial como para obligar al abandono de esta interesante teoría.
Una discusión sobre las dificultades de la teoría de Russell me llevó a emprender una investigación matemática de la estabilidad de las estrellas en general, y se encontró que [ p. 296 ] proporcionan una explicación simple y algo inesperada de la distribución de estrellas en el diagrama de Russell, que de otro modo sería incomprensible; es en resumen que las regiones desocupadas del diagrama representan estrellas en una condición inestable. No sé qué proporción de astrónomos acepta esta explicación; algunos, cuya opinión valoro, no. No creo que mucho de lo escrito hasta ahora en este libro sea cuestionado seriamente por críticos competentes, pero es justo decir que en este punto estamos entrando en un terreno controvertido.
¶ La hipótesis de las estrellas líquidas
Empecemos imaginando una enorme cantidad de estrellas construidas sobre todos los planos posibles, a partir de todo tipo de sustancias. La investigación matemática muestra que algunas de estas estrellas pueden ser incapaces de brillar con una luz constante por una o dos razones: pueden explotar, como un barril de pólvora caliente, o pueden tener una tendencia inherente a contraerse o expandirse sin límite. Que una estrella escape o no al primer escollo depende principalmente de las propiedades de la sustancia de la que está construida; si escapa a la segunda depende principalmente de la forma en que se construye. Los dos escollos no son del todo distintos, y cuando consideramos la estabilidad de las estrellas totalmente gaseosas de un peso enormemente grande, encontramos que los hoyos en los dos lados del camino se fusionan en uno, o como mucho solo una estrecha franja de terreno seguro es dejado entre ellos. Sin embargo, se sabe que existen estrellas de un peso enormemente grande, y continúan brillando constantemente. Entonces, si estas estrellas son totalmente gaseosas, deben ocupar el único lugar seguro del suelo entre los dos hoyos, y esto nos informa tanto sobre la forma en que están construidas como [< small>p. 297] de las propiedades de la sustancia de la que están hechas.
Encontramos que tales estrellas solo escapan de ambas trampas si su sustancia posee propiedades que parecen muy improbables y contrarias a cualquier cosa de la que tengamos alguna experiencia o conocimiento en física; en resumen, para que tal estrella permanezca estable, la aniquilación de su materia debe proceder a un ritmo que depende de la temperatura. Tal propiedad parece en todos los sentidos contraria a los principios físicos explicados en el Capítulo II, como lo es a todas nuestras expectativas del comportamiento atómico. La aniquilación de la materia es un cambio mucho más violento e involucra cantidades de energía mucho más altas que la mera desintegración radiactiva, y como este último proceso no se ve afectado por los cambios de temperatura, parece difícil que el proceso de aniquilación sea, en todo caso hasta alcanzar temperaturas del orden de los 2.200.000.000.000 grados tabulados en la p. 144 [4].
Sin embargo, ya hemos encontrado indicios de que las estrellas no son puramente gaseosas, ya que las masas puramente gaseosas no podrían formar sistemas binarios cerrados del tipo observado en las binarias espectroscópicas (p. 222). Dichos sistemas solo pueden formarse a partir de una masa que simule las propiedades de un líquido en lugar de las de un gas; la masa no necesita ser completamente líquida, pero debe haber una divergencia considerable del estado de un gas puro, al menos en sus regiones centrales. Más adelante también surgirá evidencia adicional en el mismo sentido (págs. 310, 311).
Tan pronto como admitimos que el interior de las estrellas no necesita estar en un estado completamente gaseoso, toda la situación cambia, incluso una ligera desviación del [ p. 298 ] estado gaseoso que imparte una gran estabilidad adicional a la estrella. Si una estrella de gran peso es puramente gaseosa en su estructura, la región de estabilidad entre los dos escollos se reduce a una franja estrecha, y solo al pisarla puede la estrella escapar de los destinos alternativos de explotar o colapsar. Pero si la estrella tiene un centro líquido, o parcialmente líquido, esta franja de tierra segura es tan ancha que, consistentemente con la estabilidad, el material estelar puede tener exactamente la propiedad que a priori deberíamos esperar encontrar, a saber, que su aniquilación procede, como la desintegración radiactiva, al mismo ritmo a todas las temperaturas. Si la sustancia de la estrella tiene esta propiedad, la estrella no puede estar en peligro de explotar, porque una masa de uranio o radio no explota hagamos lo que hagamos con ella. Y el análisis matemático muestra que si el centro de la estrella es líquido, o parcialmente líquido, no hay peligro de colapso; el centro líquido proporciona una base tan firme para la estrella que hace imposible un colapso.
Estas consideraciones sugieren las dos hipótesis complementarias:
-
Que la aniquilación de la materia estelar procede espontáneamente, no siendo afectada por la temperatura de la estrella.
-
Que las regiones centrales de las estrellas no están en un estado puramente gaseoso; sus átomos, núcleos y electrones están tan apretados que no pueden moverse libremente entre sí, como en un gas, sino que se empujan entre sí como las moléculas de un líquido.
Si hemos estado en lo correcto (p. 149) al atribuir la radiación altamente penetrante observada en la atmósfera terrestre a la aniquilación de materia en cuerpos astronómicos distantes, entonces se confirma la primera hipótesis. Porque la radiación no pudo retener su [ p. 299 ] alto poder de penetración si ya había penetrado en cualquier gran espesor de materia. La lucha de atravesar la materia alarga la longitud de onda de todo tipo de radiación (los cuantos se debilitan todo el tiempo), y así disminuye su poder de penetración. Por lo tanto, dondequiera que se originó la radiación altamente penetrante, debe haber salido al espacio vacío sin mucha lucha, y esto es lo mismo que decir que debe haberse originado en la materia a una temperatura comparativamente baja. Así, la existencia de la radiación altamente penetrante prueba que la materia puede ser aniquilada en grandes cantidades a temperaturas muy bajas; las altas temperaturas de los interiores estelares no son necesarias, como afirma la teoría de Russell, para que se produzca la aniquilación.
Un simple cálculo muestra que no puede haber una aniquilación apreciable de la sustancia terrestre. En el sol, alrededor de un átomo de cada 1019 se aniquila cada minuto; si incluso una diezmilésima parte de estos átomos fueran aniquilados en la tierra, su superficie sería demasiado caliente para la habitación humana. Ya no podemos explicar esto diciendo que el sol es caliente y la tierra fría, de modo que la aniquilación continúa en el primero pero no en el segundo. Más bien debemos suponer que los átomos del sol son de un tipo diferente de los de la tierra. Los átomos solares se aniquilan espontáneamente, los átomos terrestres no, o al menos no lo hacen en grado apreciable.
La segunda de nuestras hipótesis, que las regiones centrales de las estrellas se parecen más a un líquido que a un gas, es, como hemos visto, una consecuencia necesaria de la primera, pero la evidencia independiente a su favor se encuentra en la formación de sistemas binarios por fisión. Porque en el capítulo IV (p. 222) vimos que una estrella sólo podía romperse por fisión si tenía un centro líquido o casi líquido.
[ p. 300 ]
¶ La estabilidad de las estructuras estelares
Por el momento, aceptemos tentativamente la hipótesis de que la generación de energía estelar ocurre espontáneamente, como la desintegración de átomos radiactivos. Los átomos que son responsables de la luz y el calor de las estrellas pueden considerarse átomos súper radiactivos que se aniquilan espontáneamente y así transforman su sustancia en radiación.
Ya hemos visto que, según esta visión del mecanismo de generación de energía estelar, una estrella sólo puede continuar brillando constantemente si sus regiones centrales no están en una condición puramente gaseosa. Una estrella construida sobre cimientos de gas altamente comprimible corre el mismo destino que una casa construida sobre arena: se derrumba. Una estrella puramente gaseosa es una estructura dinámicamente inestable y debe contraerse continuamente hasta que los átomos en sus regiones centrales estén tan apretados que su estado ya no pueda considerarse gaseoso. Entonces, y solo entonces, la estrella podrá existir permanentemente como una estructura estable. Así, las regiones centrales de cualquier estrella permanente real, el sol por ejemplo, debe estar en un estado que, por brevedad, podemos describir como líquido.
Ahora imaginemos que el sol se expande diez veces su diámetro actual. Esto disminuiría su densidad a una milésima parte de su valor original. El sol real es un 40 por ciento más denso que el agua, pero el sol expandido solo sería tan denso como el aire atmosférico ordinario. Los átomos y los electrones, habiéndose separado diez veces más, estarían tan distantes entre sí que el nuevo sol podría considerarse totalmente gaseoso. Por lo tanto, sería dinámicamente inestable y no podría permanecer en su estado completamente gaseoso.
[ p. 301 ] Nuestro sol imaginario expandido, por supuesto, ya no es una estrella de secuencia principal en el diagrama de Russell. Al expandir el sol a diez veces su tamaño actual, lo sacamos de la secuencia principal a una región completamente desprovista de estrellas; de hecho, al gran abismo que se encuentra entre las gigantes rojas y las enanas rojas (ver fig. 22, p. 278). Por lo tanto, parece que incluso si colocamos deliberadamente una estrella en esta región, no se queda allí sino que se contrae inmediatamente hasta que llega a la secuencia principal. ¿No podría esto explicar por qué la región en cuestión no está habitada por estrellas?
A continuación, imaginemos el sol contraído a una décima parte de su diámetro actual, de modo que sus átomos y electrones se muevan diez veces más cerca unos de otros. Su densidad media aumenta así de 1,4 a 1400 veces la del agua, y su densidad central de aproximadamente 140 a 140.000. Puedes verificarme aquí señalando que si el sol ya está en estado líquido, no puede comprimirse hasta tal punto; por lo general, la densidad de un líquido no puede aumentar mil veces. Pero ya hemos notado que reducir a la mitad el diámetro de una estrella duplica su temperatura en todas partes. Del mismo modo, al reducir el diámetro de una estrella a una décima parte, su temperatura se multiplica por diez, de modo que la temperatura central del Sol aumentará, digamos, de 50 millones de grados a 500 millones de grados. Y a esta última temperatura, los átomos ya casi no existen como tales: la materia estelar se compone casi por completo de electrones y núcleos libres. Y estos son tan diminutos que el aumento de la densidad media del sol de 1,4 a 1400 veces la densidad del agua no sólo es posible, sino que deja la sustancia del sol en un estado que puede describirse mejor como gaseoso. Una vez más, entonces, el nuevo sol es dinámicamente inestable. Sería [ p. 302 ] representado por un punto muy a la izquierda de la secuencia principal, cerca del centro de la región desocupada entre la secuencia principal y las enanas blancas, pero como es inestable no puede mantener su posición aquí. Nuevamente vemos que incluso si colocamos una estrella en esta región, no puede permanecer allí. Y, de nuevo, ¿no puede ser que la razón por la que esta región está desocupada es que representa estrellas inestables?
Una vez más puedes comprobarme. Si he resuelto mi cuestión, ha sido con la ayuda del aumento de temperatura que acompaña a la contracción. Cuando imaginamos que el sol se expandía, ¿no deberíamos haber considerado la caída de temperatura que acompaña a la expansión? La respuesta es que deberíamos, pero no habría hecho ninguna diferencia. Bajar la temperatura hará que se vuelvan a formar varios anillos L, y posiblemente también anillos M, de electrones, de modo que los nuevos átomos serán de mayor tamaño, pero no perderán su libertad de movimiento lo suficiente como para hacer el sol estable. Habría sido diferente si hubiéramos estado hablando de una estrella de 10 o 50 veces el peso del sol; entonces se puede demostrar que la reformación de los anillos K y L habría producido una serie de configuraciones estables.
Todo el problema es demasiado complicado para ser discutido satisfactoriamente de esta manera fragmentaria; su discusión adecuada implica un análisis matemático muy complicado. La discusión matemática muestra que el diagrama de Russell se puede dividir en regiones que representan configuraciones estables e inestables de la manera que se muestra en la fig. 24.
Las áreas inestables están marcadas; las áreas restantes son estables. Los puntos que forman una especie de fondo [ p. 303 ] del diagrama representan 2100 estrellas cuyas magnitudes absolutas se conocen a través de sus paralajes que se determinaron espectroscópicamente en el Monte Wilson. El material de observación no es perfecto, ya que existe una gran incertidumbre en todos los paralajes espectroscópicos de las estrellas de tipo B, y las estrellas de tipo A casi no están representadas porque es prácticamente imposible obtener sus paralajes mediante el [ p. 303] método espectroscópico. Las curvas teóricas son probablemente aún más imperfectas, sin embargo, tal como son, parecen sugerir con mucha fuerza que las regiones ocupadas y desocupadas coinciden con aquellas que representan configuraciones estables e inestables; después de hacer todas las concesiones posibles a las imperfecciones tanto de la teoría como de la observación, queda demasiado acuerdo para ser explicado como mera coincidencia.
Así, la conclusión a la que parece llevar la discusión matemática es que las regiones ocupadas en el diagrama de Russell representan estrellas cuyas regiones centrales están en estado líquido o casi líquido. Todas las demás estrellas son inestables, por lo que las regiones correspondientes en el diagrama de Russell están necesariamente vacías. Para decirlo en un lenguaje menos técnico, todas las estrellas del cielo deben tener centros líquidos o casi líquidos.
Aquí tenemos una pieza del rompecabezas que parece encajar con la pieza que desenterramos en el Capítulo IV, donde descubrimos que una estrella solo podía romperse por fisión si tenía un centro líquido o casi líquido. Se acumula evidencia de que las estrellas tienen centros líquidos en lugar de gaseosos.
La crítica a la hipótesis anterior, generalmente descrita como la hipótesis de la «estrella líquida», ha tomado principalmente la forma de que los diámetros de los anillos K de los átomos son tan pequeños que los átomos del anillo K en las regiones centrales del sol no pueden ser empaquetados lo suficientemente próximos como para implicar cualquier desviación sustancial del estado gaseoso. Es difícil discutir, y aún más enfrentar, esta crítica sin conocer los diámetros precisos de estos átomos del anillo K. Por supuesto, conocemos los diámetros asignados al anillo K por la teoría de Bohr (p. 129), pero ya nadie sostiene que esta teoría proporcione una imagen real del átomo. Proporciona [ p. 305 ] un buen modelo de trabajo dentro de los límites, pero no sabemos dónde terminan los límites. La única experiencia práctica que tenemos de los átomos del anillo K es con los átomos de helio; la teoría de Bohr les asigna un diámetro de 0,54 x 10-8 cm. Sin embargo, el helio sólido y el líquido proporcionan una ilustración práctica de la proximidad con la que se pueden empaquetar los átomos de helio; en estos cada átomo ocupa una esfera de 4 x 10-8 cm de diámetro, o más de 400 veces el espacio que le asigna la teoría de Bohr. Parece como si todavía estuviéramos lejos de un conocimiento definitivo de las dimensiones de los anillos K de electrones.
La nueva mecánica ondulatoria de Schrödinger dibuja una imagen muy diferente de los interiores atómicos de la teoría más simple de Bohr, a la que está reemplazando rápidamente. Incluso el electrón es algo muy diferente del electrón de la vieja teoría de Bohr. Es el electrón pasado de moda sólo cuando está a una distancia infinita del núcleo. A medida que se acerca gradualmente a este núcleo, sufre una metamorfosis de un tipo que nadie ha logrado describir todavía, y es completamente imposible decir qué forma puede haber asumido cuando está haciendo lo que llamamos «describir una órbita K del anillo». Todo lo que sabemos sobre la órbita del anillo K es su energía, y parece imposible predecir la cantidad de espacio ocupado por tal órbita hasta que tengamos un mejor conocimiento de las cualidades del artículo que la describe.
Por supuesto, tenemos que admitir que la evidencia física, tal como es, parece apuntar a que los átomos del anillo K son sustancialmente más pequeños de lo que se necesita para la hipótesis de la estrella líquida. Pero la evidencia astronómica me parece más fuerte y confiable, y apunta exactamente en la dirección opuesta. Y aquí debemos dejar el rompecabezas hasta que salgan a la luz más piezas.
[ p. 306 ] Hasta que sepamos el tipo de átomos que componen una estrella en particular, no podemos calcular hasta qué punto se descompondrán por la temperatura del interior de la estrella. Como consecuencia, las curvas teóricas de demarcación entre configuraciones estables e inestables no pueden calcularse sin asumir números atómicos definidos para los átomos estelares.
Las curvas mostradas en la fig. 24 se han dibujado para un número atómico de alrededor de 95, que es ligeramente superior al número atómico, 92, del uranio. Se seleccionó este número atómico porque se encontró que producía la mejor concordancia entre la teoría y la observación, pero veremos que otras consideraciones justifican nuestra elección.
¶ Estructura estelar
Una estrella, como una casa o un montón de arena, es una estructura que colapsaría por su propio peso si cada capa no se mantuviera contra la gravedad por la presión que la siguiente capa interna de la estrella ejerce sobre ella. Esta presión no es, como la presión del gas ordinario, el resultado de los impactos de moléculas completas. Se produce en parte por el impacto de un cierto número de átomos que han sido despojados de electrones casi o completamente hasta sus núcleos, pero en mucha mayor medida por el impacto de una lluvia de electrones libres. En las estrellas masivas, se produce una presión adicional por el impacto de la radiación que, como hemos visto, lleva peso consigo y, por lo tanto, ejerce presión sobre cualquier obstáculo que encuentre. Los impactos combinados de electrones libres, de átomos (o núcleos desnudos),
[ p. 307 ] Esto proporciona una imagen instantánea razonablemente buena de la estructura de una estrella. La imagen correspondiente de su mecanismo se obtiene pensando en los núcleos como partículas de rayos α, en los electrones libres como partículas de rayos β y en la radiación como rayos γ (aunque en la mayoría de las estrellas la mayor parte de la radiación tiene la longitud de onda de los rayos X). Todos estos se abren camino a través de la estrella y, precisamente como en el trabajo de laboratorio, los rayos β son más penetrantes que los rayos α, y los rayos γ son más penetrantes que cualquiera de los dos.
El transporte de energía en una estrella. Hemos visto cómo el calor de un gas es simplemente la energía de su movimiento molecular. La conducción del calor en un gas suele estudiarse considerando cada molécula como portadora de energía; cuando choca con una segunda molécula, la energía de las dos moléculas que chocan se redistribuye entre ellas y, de esta manera, el calor se transporta de las regiones más calientes a las más frías. Cada molécula tiene un poder de transporte que es conjuntamente proporcional a su energía de movimiento, su velocidad de movimiento y su «camino libre»: la distancia que recorre entre colisiones sucesivas.
En el interior de una estrella, hay tres tipos distintos de portadores en acción: átomos (o núcleos desnudos), electrones libres y radiación. Podemos comparar sus capacidades relativas como portadores multiplicando la energía, las velocidades y los caminos libres de cada uno. Para este propósito, el «camino libre» de la radiación puede tomarse como la distancia que recorre la radiación antes de que el 37 por ciento de ella haya sido absorbida, ya que puede demostrarse que esta es la distancia promedio que transporta su energía. Al realizar el cálculo, se encuentra que la capacidad de carga tanto de los núcleos como de los electrones es insignificante en comparación con la de la radiación. Los núcleos [ p. 308 ] y los electrones pueden tener la mayor cantidad de energía para transportar, pero debido a sus poderes de penetración más débiles, la distancia que recorren, su recorrido libre, es mucho menor que la de la radiación. Su velocidad de transporte también es menor, ya que la radiación transporta su energía con la velocidad de la luz. Así ocurre que prácticamente todo el transporte de energía desde el interior de una estrella hasta su superficie es por el vehículo de la radiación.
Este principio general fue establecido claramente por primera vez por Sampson en 1894. También mostró cómo la temperatura de cualquier pequeño fragmento del interior de una estrella debe determinarse por la condición de que recibe tanta radiación como la que emite, pero sus aplicaciones detalladas estaban viciadas por su uso de una ley de radiación errónea. Doce años más tarde, Schwarzschild presentó de forma independiente la misma idea y la expresó en ecuaciones matemáticas de «equilibrio radiativo» que han formado la base de todas las discusiones posteriores sobre el problema.
Solo porque la radiación supera por completo a los átomos y electrones en el transporte de energía desde el interior de una estrella hasta su superficie, se deduce que la construcción de una estrella debe estar determinada por la opacidad de la materia en su interior. Si se altera esto, se altera el poder portador de la radiación, y esto afecta a toda la estructura de la estrella. Una estrella cuyo interior fuera completamente transparente no podría retener nada de calor; todo su interior estaría a muy baja temperatura y la estrella sería de una extensión enorme. En cambio, en una estrella muy opaca, toda la energía quedaría acumulada en el lugar donde se generó, por lo que la temperatura interior sería muy alta y el diámetro de la estrella sería [ p. 309 ] correspondientemente pequeño.
Desafortunadamente, es imposible obtener ningún tipo de medida directa de la opacidad de la materia estelar. Ni siquiera podemos medir la opacidad de la materia terrestre en condiciones estelares, ya que el interior de las estrellas está a temperaturas incomparablemente más altas que las disponibles en el laboratorio. Sin embargo, sabemos que la opacidad de la materia estelar se debe a que los átomos, núcleos y electrones libres que la componen frenan el viaje de la radiación, y aunque no podemos obtener una muestra de la materia estelar, sabemos con bastante certeza cuántos átomos, núcleos y electrones que tal muestra contendría. Por lo tanto, se convierte en una cuestión de cálculo teórico para determinar su opacidad.
Tal cálculo fue realizado por el Dr. Kramers de Copenhague en 1923, y sus resultados ganaron aceptación general. Muy recientemente, el Sr. Gaunt de Cambridge ha hecho un cálculo mucho más refinado y ha obtenido resultados que concuerdan mucho con los que originalmente dio Kramers. En la medida en que estos resultados pueden probarse en el laboratorio, concuerdan bien con la observación. Y, aunque existe una gran brecha entre las condiciones de laboratorio y las condiciones estelares, es difícil ver cómo la fórmula de Kramers podría fallar en las estrellas.
A partir de esta fórmula podemos determinar completamente la construcción de las estrellas o, si se supone que se conoce la construcción de la estrella, la fórmula de Kramers nos dice la velocidad a la que fluye la energía hacia su superficie (esto depende completamente de la opacidad de la sustancia de la estrella), y esto a su vez nos dice a qué velocidad se debe generar energía dentro de la estrella para que pueda permanecer [ p. 310 ] en equilibrio en la configuración en cuestión. Como era de esperar, se encuentra que las configuraciones de diferentes diámetros requieren diferentes tasas de generación de energía. En la naturaleza, una estrella debe ajustar su diámetro para adaptarse a la velocidad a la que genera energía; al hacerlo, fija no solo su diámetro sino también su temperatura superficial, color y tipo espectral.
Cálculos detallados muestran que, para estrellas totalmente gaseosas, los diámetros grandes corresponden a una débil generación de energía y viceversa. Así, si las estrellas fueran totalmente gaseosas, las gigantes rojas serían menos luminosas que las estrellas de secuencia principal del mismo peso. El Diagrama de Seares, reproducido en la p. 282, muestra que en realidad ocurre lo contrario, una gigante roja que emite de 10 a 20 veces más radiación total que una estrella de secuencia principal igualmente masiva. Esto proporciona evidencia en contra de que las estrellas sean totalmente gaseosas, pero hay evidencia más sólida que esta. Para estrellas totalmente gaseosas, las líneas gruesas que se muestran en el diagrama de Seares serían líneas rectas oblicuas, inclinadas hacia arriba a la izquierda. La amplia divergencia entre tal sistema de líneas oblicuas y las curvas mostradas en la fig. 23 da alguna indicación de la medida en que la condición de la materia estelar diverge del estado puramente gaseoso.
De acuerdo con la teoría de Kramers, la opacidad de la materia depende de los números atómicos y los pesos atómicos de los átomos que la componen; un gran coágulo de materia en forma de núcleo atómico masivo es mucho más efectivo para absorber radiación que un gran número de pequeños coágulos del mismo peso [ p. 311 ] total. La experiencia terrestre cotidiana muestra que esto es así. Por esta razón, tanto el físico como el cirujano eligen el plomo como material con el que apantallar su aparato de rayos X; descubren que una tonelada de plomo es mucho más eficaz para detener los rayos X no deseados que una tonelada de madera o de hierro. Si conociéramos la resistencia de un aparato de rayos X y el peso total del material de protección que lo rodea, podríamos formar una estimación muy justa del peso atómico del material de protección midiendo la cantidad de radiación X que escapaba a través de él.
Se puede utilizar un método muy similar para determinar los pesos atómicos de los átomos que componen las estrellas. En efecto, una estrella no es más que un enorme aparato de rayos X. Conocemos los pesos de muchas de las estrellas, y la velocidad a la que generan rayos X es simplemente la velocidad a la que irradian energía hacia el espacio. Si pudiéramos dividir cada núcleo atómico de una estrella en dos mitades, deberíamos reducir a la mitad la opacidad de la estrella, de modo que la radiación viajara el doble de distancia a través de la estrella antes de ser absorbida. Si la estrella fuera totalmente gaseosa, esto daría como resultado que se expandiera cuatro veces su diámetro original y que la temperatura de su superficie se redujera a la mitad. De ello se deduce que podemos calcular el peso atómico de los átomos que componen una estrella a partir del peso, la luminosidad y la temperatura superficial de la estrella.
Los pesos atómicos de varias estrellas, que calculé sobre la suposición de que las estrellas eran totalmente gaseosas, resultaron en prácticamente todos los casos más altos que el del uranio, que es el átomo más pesado conocido en la tierra. No sólo demostraron ser más altos, sino enormemente más altos; tan alto de hecho, como para parecer completamente improbables. Una vez más, la explicación parece [ p. 312 ] ser que las estrellas no son totalmente gaseosas. Tan pronto como se supone que los interiores estelares son parcialmente líquidos, los pesos atómicos calculados se reducen enormemente. Ya no se pueden determinar con exactitud, pero el número atómico de alrededor de 95 al que nos llevó la consideración del diagrama de Russell parece ser totalmente consistente con todos los hechos conocidos.
De hecho, otras consideraciones parecen sugerir que los números atómicos de los átomos estelares deben ser superiores a 92. A priori, la radiación estelar podría originarse en tipos de materia que conocemos en la Tierra o en otros tipos desconocidos. Una vez que se acepta que la alta temperatura y la densidad no pueden hacer nada para acelerar la generación de radiación por parte de la materia ordinaria, queda claro que la radiación estelar no puede originarse en los tipos de materia que conocemos en la Tierra. Deben existir otros tipos de materia, y como, con dos excepciones, todos los números atómicos hasta el 92 (uranio) ya están ocupados por elementos terrestres, parece probable que estos otros tipos deban ser elementos de mayor peso atómico que el uranio.
No debe esperarse que estos átomos superpesados revelen su presencia en los espectros estelares, ya que éstos sólo nos informan sobre la constitución de las atmósferas de las estrellas. Y como los átomos más ligeros flotan hacia la parte superior, son estos, en su mayoría, los que figuran en los espectros estelares. Si la atmósfera del sol hubiera contenido un número considerable de átomos superpesados cuando nacieron los planetas, algunos de ellos aún deberían existir en la tierra. No puede haber un gran número, o su alta generación de energía los traicionaría. La opinión más simple parece ser que los átomos más pesados se hunden en el centro de las estrellas, y que la tierra se formó principal o exclusivamente a partir de los átomos más ligeros que habían flotado hacia la superficie del sol.
¶ Evolución estelar
Hemos supuesto que las estrellas nacieron inicialmente como condensaciones en las franjas exteriores de las nebulosas espirales. Estas condensaciones serían, por el modo de su formación, necesariamente de todo tipo de tamaños, y sujetas sólo a la única restricción de que ninguna de ellas podría estar por debajo de un cierto límite de peso. Por lo tanto, no debemos esperar que las estrellas, ya sea al nacer o posteriormente, sean todas del mismo tamaño o peso, o todas en la misma condición física. Las estrellas comenzarían su existencia en diferentes puntos del diagrama de Russell, pero podemos imaginar que sus posiciones iniciales están limitadas a aquellas partes del diagrama que pueden estar ocupadas por estrellas, ya sea, como sugeriría la hipótesis de la estrella líquida, porque estas son las únicas configuraciones estables, o bien por alguna otra razón hasta ahora desconocida. Cada año, una estrella pierde una cierta cantidad de peso, y su tasa de generación de energía, y también su luminosidad, se reducen correspondientemente, con el resultado de que se mueve a una nueva posición en el diagrama. Volviendo al diagrama de pesos estelares de Seares en la p. 282, podemos pensar en las curvas de igual peso como un tramo de escalones (es cierto que escalones muy desiguales), cada uno de los cuales representa un peso menor que el anterior. Cualquiera que sea la evolución de una estrella, es esencial que siempre sea hacia abajo: cualquier paso hacia arriba es imposible.
Podemos trazar dos caminos posibles de evolución estelar en el diagrama de Russell que no implican la entrada en regiones no ocupadas por estrellas: dos caminos por los que el ejército estelar puede marchar a medida que transforman su sustancia en radiación. La primera es, por supuesto, la «secuencia principal», que un gran número de consideraciones sugieren que es la línea principal de marcha del ejército estelar. La rama que comienza desde las [ p. 314 ] gigantes rojas en el diagrama de Russell representan una segunda posible línea de marcha, un cierto número de estrellas viajando a lo largo de esta rama hasta que alcanzan la secuencia principal como estrellas azules o blancas, y luego viajando por la mitad inferior de la secuencia principal para terminar como débiles estrellas rojas que pasan a la extinción final.
El progreso a lo largo de cada uno de estos caminos va acompañado de una reducción continua en el tamaño de la estrella, y su diámetro disminuye constantemente. Esto no es lo mismo que decir que la densidad de la estrella aumenta continuamente, ya que la estrella disminuye continuamente de peso, de modo que incluso si la densidad de la estrella se mantuviera igual, su diámetro disminuiría. No obstante, un estudio de las determinaciones de Seares de las densidades medias, como se muestra en el diagrama de la p. 282, sugiere que hay un aumento continuo de densidad, aunque esto se vuelve muy leve en los tramos medios de la secuencia principal.
Prácticamente todas las teorías de evolución estelar que se han propuesto alguna vez han imaginado que la marcha del ejército estelar es del mismo tipo general que la que acabamos de describir, aunque quizás la opinión actual se incline a tratar la secuencia principal como la línea principal de marcha, mientras que las teorías anteriores suponían que las estrellas más jóvenes marchaban únicamente a lo largo de la rama de la gigante roja, y solo se unían a la secuencia principal con la mediana edad. La primera teoría seria de todas, la de Lockyer, se expresó en términos de ramas de temperatura ascendente y descendente, formando juntas la última línea de marcha mencionada en el diagrama de Russell. Una teoría que Russell propuso en 1913 asignó nuevamente a las estrellas las líneas de marcha que acabamos de describir. También intentó una explicación física, ya abandonada, de por qué las estrellas seguían estos [ p. 315 ] caminos particulares en lugar de otros. Su teoría más reciente de 1925 solo difería de su teoría anterior en dar la nueva explicación, que ya hemos discutido (p. 293), de por qué las estrellas siguieron estos caminos particulares.
En la actualidad, probablemente sea justo decir que casi todos los astrónomos, y tal vez todos, están de acuerdo en que las trayectorias evolutivas de las estrellas son del tipo general que hemos descrito. Algunas estrellas comienzan como gigantes rojas, algunas como azules, algunas posiblemente en condiciones intermedias. A medida que envejecen, todos se mueven hacia abajo en el diagrama de Russell, sus diversas trayectorias convergen en un punto en la bifurcación de la γ invertida que se muestra en la fig. 22, y después de pasar este punto se mueven hacia abajo en la secuencia principal. Por otro lado, existe la más amplia diferencia de opinión en cuanto a la interpretación física que debe asignarse a estos caminos. La mayoría de los astrónomos probablemente están suspendiendo el juicio hasta que se obtenga alguna evidencia observacional definitiva para decidir entre teorías en conflicto.
Cuando las estrellas aparecieron por primera vez como motas de rocío ardiente arrojadas por nebulosas giratorias, consistían en mezclas de átomos de todo tipo, algunos de los cuales quizás tenían una vida tan corta que se transformaban casi de inmediato en radiación, y otros tenían tal larga vida que podrían describirse apropiadamente como permanentes. Excepto por un pequeño número de átomos radiactivos, la tierra debe consistir enteramente de átomos de este último tipo. Los cálculos muestran que los átomos terrestres deben tener una vida mucho más larga que el átomo estelar promedio, de lo contrario, su autoaniquilación haría que la Tierra fuera demasiado caliente para ser habitada. Los átomos permanentes en una estrella no contribuyen casi en nada a su capacidad de generación de energía, por lo que simplemente se suman a su [ p. 316 ] peso. Los átomos de vida más corta de todos contribuyen en gran medida a la generación de energía de la estrella y añaden muy poco a su peso. En general, cuanto más corta es la vida de cualquier tipo de átomo, mayor es la proporción de su número aniquilado por año y, por lo tanto, mayor es la cantidad de energía que genera por tonelada de peso.
Una estrella comienza su vida con una gran proporción de átomos de vida corta, y así al principio genera furiosamente energía. A medida que envejece, los átomos de vida más corta desaparecen primero y, al hacerlo, reducen la generación de energía promedio de la estrella por tonelada, de modo que, a medida que disminuye el peso de una estrella, también debe hacerlo su tasa de generación de energía por tonelada. Finalmente han desaparecido todos los átomos con mucha capacidad generadora de energía, y queda la estrella, una masa reducida y disminuida de átomos que tienen muy poca capacidad para generar radiación.
Dicho de otro modo, la tasa a la que una estrella genera energía por tonelada es proporcional a la tasa de mortalidad de su población de átomos. Decir que Sirio genera 16 veces más energía por tonelada que el sol es solo otra forma de decir que el átomo promedio en Sirio tiene solo un dieciseisavo de la expectativa de vida de los átomos solares; su tasa de mortalidad es 16 veces mayor. A medida que los tipos de átomos que tienen la tasa de mortalidad más alta mueren gradualmente en cualquier estrella, la tasa de mortalidad promedio de la población disminuye o, en otras palabras, a medida que una estrella envejece, su capacidad de generación de energía por tonelada disminuye.
Esto está de acuerdo con los hallazgos de la astronomía observacional. Las estrellas más masivas no sólo generan más energía que las estrellas menos masivas, como en todo caso es de esperar; también generan enormemente más energía por tonelada. Esto se ilustra con la siguiente lista de estrellas de la secuencia principal:
[ p. 317 ]
| Estrella | Peso (en términos de sol) | Generación de energía (ergios por gramo) |
|---|---|---|
| Estrella A de Pearce | 36,3 | 15.000 |
| V Puppies A | 19,2 | 1.000 |
| Sirio A | 2,45 | 29 |
| sol | 1,00 | 1,90 |
| ε Eridani | (0,45) | 0,26 |
| Kruger 60B | 0,20 | 0,021 |
El diagrama de pesos estelares de Seares (p. 282) muestra que ésta es una propiedad general de las estrellas. Para repetir nuestra metáfora anterior, las estrellas despilfarran su sustancia pródigamente en su juventud, mientras les queda mucho para gastar, pero la parsimonia les sobreviene con la vejez. Las consideraciones teóricas nos han dado ahora una explicación de este fenómeno.
El mismo diagrama muestra que dos estrellas del mismo peso no suelen tener la misma luminosidad. En general, las estrellas gigantes en la rama en espuela que conduce a las gigantes rojas tienen luminosidades sustancialmente más altas que las estrellas de la secuencia principal del mismo peso. Ya hemos notado cómo una gigante roja puede emitir hasta 10 o 20 veces la radiación de una estrella de secuencia principal igualmente masiva. La misma historia se repite cuando pasamos de las estrellas de la secuencia principal a las enanas blancas. Las estrellas de la secuencia principal emiten mucha más radiación, hasta 500 veces más, que las enanas blancas del mismo peso. Esto se ilustra con las siguientes tres enanas blancas, que pueden compararse con las últimas tres estrellas de la tabla anterior:
| Estrella | Peso (en términos de sol) | Generación de energía (ergios por gramo) |
|---|---|---|
| Sirio B | 0,85 | 0,0027 |
| ο2 Eridani B | 0,44 | 0,002 |
| la estrella de van Maanen | (0,20) | (0,00055) |
[ p. 318 ] Hasta ahora hemos supuesto que la generación de energía es espontánea y, por lo tanto, no se ve afectada por los cambios en las condiciones físicas. Sin embargo, los hechos que acabamos de mencionar parecen sugerir que esto difícilmente puede ser toda la verdad del asunto. Para plantear la objeción en términos de un caso concreto, Sirio A y su compañera enana blanca Sirio B con toda probabilidad deben haber nacido al mismo tiempo de la misma nebulosa (p. 284), sin embargo, el primero genera 4000 veces más energía por tonelada que este último. Parece improbable que una diferencia tan grande pueda atribuirse a diferentes tipos de átomos; el origen común de las dos estrellas casi lo impide. Sabemos que los átomos están en diferentes condiciones físicas en las dos estrellas; en Sirio A han conservado sus anillos K intactos, mientras que en Sirio B, la enana blanca, están completamente fragmentados en núcleos desnudos y electrones libres. Si los dos componentes de Sirio consisten esencialmente en los mismos tipos de átomos, como su origen común nos llevaría a esperar, entonces la enorme diferencia en las tasas a las que estos átomos generan energía parecería depender de las diferentes condiciones físicas de sus átomos.
Las consideraciones presentadas en el Capítulo III hacen muy probable que la tasa de generación de energía de una estrella dependa de la condición física de sus átomos. Allí supusimos que la energía estelar se generaba a través de electrones que se fusionaban con protones; los protones existen sólo en los núcleos atómicos, y consideraciones puramente físicas llevaron a la conjetura de que los únicos electrones que pueden fusionarse con un protón en particular son aquellos que describen momentáneamente órbitas alrededor del núcleo en el que reside el protón. Un estudio de la estructura estelar apoya esta hipótesis, ya que si la energía pudiera ser generada por la caída de electrones libres [ p. 319 ] en núcleos, se puede demostrar que toda la estrella sería inestable y explotaría en un destello de radiación. Según esta hipótesis, una estrella en la que sólo unos pocos átomos tienen electrones en movimiento orbital puede, por supuesto, generar muy poca energía. Esto explica a la vez los débiles poderes de generación de energía de las enanas blancas, y también da una idea de por qué las gigantes rojas, en las que sobreviven los anillos de electrones L y M, generan más energía que las estrellas de la secuencia principal de igual peso.
A medida que una estrella envejece y su peso disminuye, tiene que elegir continuamente nuevas configuraciones, como hacer que su emisión de energía sea igual a su tasa interna de generación de energía. La misma estrella puede ser una gigante roja, una estrella de secuencia principal y una enana blanca a su vez. Despojado de tecnicismos, esto significa que una estrella ajusta continuamente su diámetro para adaptarse a su ritmo variable de generación de energía.
Según la hipótesis que acabamos de considerar, una estrella altera tanto su emisión como su generación de energía al cambiar su diámetro. En cada instante tiene que seleccionar un diámetro para el cual los dos se equilibren exactamente. La estrella tiene un rango tan grande de tasas de generación, según le queden pocos o muchos electrones en movimiento orbital, que es probable que siempre pueda encontrar una configuración de equilibrio. En cualquier caso, todas las estrellas en el cielo parecen haberlo hecho, con la excepción de las variables de período largo que se expanden y contraen continuamente como si no pudieran encontrar un diámetro en el que su ingreso y gasto de energía se equilibraran.
Esta misma hipótesis hace posible inmediatamente que toda la gran variedad de estrellas del sistema galáctico tengan aproximadamente la misma edad, y por tanto hayan [ p. 320 ] nacido todas de la misma nebulosa. Las estrellas galácticas más luminosas difícilmente pueden haber estado generando energía a su ritmo actual durante más de unos 100.000 millones de años; cualquier edad más larga requeriría un peso imposiblemente alto para empezar. Sin embargo, los movimientos de las estrellas indican que incluso estas estrellas altamente luminosas deben haber existido durante al menos 50 veces este período. La aparente contradicción desaparece si admitimos que la extrema luminosidad de las estrellas más brillantes puede ser un desarrollo reciente, y que quizás para el 98 por ciento, de su vida, una estrella de este tipo estaba perdiendo muy poca energía porque la mayoría de sus átomos estaban despojados de electrones y, por lo tanto, eran inmunes a la aniquilación. La proporción requerida del 98 por ciento puede parecer sospechosamente grande, pero hemos expuesto un caso extremo; sólo necesitamos exigir una proporción tan grande en el caso de un tipo de estrella muy raro: probablemente no más de una estrella entre diez millones sea de ese tipo.
En su estado inactivo anterior, estas estrellas, que ahora son tan luminosas, habrían sido enanas blancas de enorme peso. La astronomía observacional no proporciona evidencia de que existan tales estrellas, pero ciertamente no hay evidencia de que no existan. Se sabe que las estrellas muy masivas son objetos muy raros, por lo que con toda probabilidad tendríamos que viajar una gran distancia desde el sol antes de encontrar una, y entonces podría estar tan lejos como para ser invisible desde la tierra. En cualquier caso, una estrella muy distante de débil luminosidad sería muy probable que escapara a la detección. No podríamos inferir que no existieran tales estrellas por el hecho de que aún no se ha encontrado ninguna.
Además, está lejos de ser absolutamente seguro que tales estrellas no hayan sido encontradas. Enanas blancas muy masivas [ p. 321 ] deberían tener temperaturas superficiales más altas que las estrellas masivas de la secuencia principal o que las conocidas enanas blancas, todas las cuales son de poco peso. Se conoce un grupo completo de estrellas, las estrellas de tipo O, cuyos espectros indican temperaturas realmente muy altas. Suelen interpretarse como estrellas de enorme luminosidad a enormes distancias, pero es posible que al menos algunas de ellas sean estrellas de débil luminosidad a distancias moderadas. En particular, las estrellas centrales de las nebulosas planetarias son de los tipos O y B. Pero mientras que la estrella normal de la secuencia principal de estos tipos espectrales es generalmente unas mil veces más luminosa que el sol, se encuentra que las estrellas centrales de las nebulosas planetarias son considerablemente menos luminosas que el sol. El Dr. Gerasimovic ha demostrado recientemente que 52 de estas estrellas tienen una luminosidad media de sólo dos tercios de la del sol. Otros observadores han encontrado luminosidades aún más bajas. Como las temperaturas superficiales de estas estrellas deben ser del orden de 30.000 grados, deben ser diminutas en tamaño; de hecho, un simple cálculo muestra que difícilmente pueden tener más de una décima parte del radio del sol.
No solo son de pequeño tamaño, sino que hay indicios de que son de gran peso. La evidencia espectroscópica muestra que, en muchos casos, las nebulosas circundantes están en rotación y, al igual que con la galaxia (p. 69) y las enormes nebulosas extragalácticas (p. 71), sus pesos pueden calcularse a partir de sus velocidades de rotación observadas. Estos parecen indicar pesos promedio de algo así como 40 o 50 veces el peso del sol. Campbell y Moore, del Observatorio Lick, han calculado que la nebulosa planetaria NGC 7009 debe tener 162 veces el peso del sol, pero muchos factores se combinan para hacer que esta estimación sea bastante incierta.
[ p. 322 ] Todo esto sugiere que las estrellas centrales de las nebulosas planetarias deben, con toda probabilidad, ser consideradas como «enanas blancas» de enorme peso. Parece posible que sean exactamente el tipo de estrella que necesita nuestra teoría. Las 52 nebulosas planetarias ya mencionadas tienen la misma distancia media al sol, y la misma distribución con respecto a la galaxia, que las estrellas tipo O, por lo que es posible que las estrellas tipo O y las nebulosas planetarias sean formas asumidas ya sea sucesivamente o alternativamente en el curso de la evolución de cuerpos similares. Cabe mencionar que las nebulosas planetarias exhiben desplazamientos espectrales que, si se interpretan de la manera ordinaria, indicarían que se están moviendo a velocidades muy altas, en algunos casos llegando a cientos de millas por segundo. Tales velocidades serían completamente inapropiadas para estrellas de gran peso. Sin embargo, esta objeción se derrota a sí misma, porque si los cambios espectrales realmente surgieron de las altas velocidades de movimiento, la más alta de las velocidades observadas sería suficiente para llevar a las nebulosas planetarias que las poseen fuera del sistema galáctico por completo; serían viajeros fortuitos a través de nuestro sistema de estrellas, mientras que su disposición y concentración ordenadas cerca del plano galáctico sugiere con fuerza que son miembros permanentes de él. Así, los grandes desplazamientos observados de las líneas espectrales difícilmente pueden indicar grandes velocidades en el espacio; se debe encontrar alguna otra interpretación. El profesor Perrine considera que surgen principalmente de los movimientos internos, la contracción, la expansión y la rotación de las nebulosas. Si es así, los movimientos en el espacio no se pueden determinar, pero al menos ya no presentan ninguna dificultad. Si estas estrellas son, como requiere nuestra hipótesis, enanas blancas de muy gran peso y pequeño radio, sus espectros deberían [ p. 323 ] exhibir un desplazamiento de la relatividad al rojo del mismo tipo que el observado realmente en Sirius B. Es posible que se encuentre que esto presenta una dificultad más seria, aunque también es posible que nuevamente pueda resultar fusionado en los grandes desplazamientos observados.
A la vista de todo esto, parece bastante posible que tanto las nebulosas planetarias, como otras estrellas de tipo O o B de débil luminosidad, puedan ser estrellas muy masivas en el estado latente contemplado por la hipótesis que acabamos de discutir. En resumen, imaginamos que una estrella masiva puede conservar su peso al existir como una nebulosa planetaria o una estrella enana tipo O durante millones de millones de años, y luego estallar como una estrella muy luminosa con toda la apariencia de extrema juventud. Pero en la actualidad hay evidencia observacional insuficiente a favor o en contra de tal hipótesis. Faltan algunas piezas del rompecabezas, y solo podemos esperar hasta que aparezcan.
Enanas blancas. Aparte de estas hipotéticas enanas blancas masivas, los astrónomos generalmente consideran a las enanas blancas ordinarias como la etapa final de la evolución estelar. Existe un acuerdo general de que son estrellas con temperaturas centrales tan altas que sus átomos están despojados de electrones, pero no hay un consenso general de opinión sobre por qué las estrellas se encogen a esta condición.
En la hipótesis de la estrella líquida, las regiones desocupadas en el diagrama de Russell representan configuraciones inestables. Por lo general, una ligera pérdida de peso de una estrella simplemente la mueve a una nueva posición en el diagrama contigua a la anterior. A veces, sin embargo, este ligero movimiento puede llevar a la estrella a una región inestable del diagrama, en cuyo caso [ p. 324 ] se apresurará por esta región, hasta que finalmente termine en una configuración estable completamente diferente.
La hipótesis de la estrella líquida explica el estado de enana blanca simplemente como el estado final al que una estrella se reduce cataclísmicamente cuando su generación de energía ya no es suficiente para darle derecho a un lugar en la secuencia principal. En este estado, la estrella irradia tan poca energía que la aniquilación y la decadencia están casi completamente controladas. Hemos visto que si el sol siguiera radiando al ritmo actual durante 15 millones de millones de años, todo su peso se transformaría en radiación. Por el contrario, la estrella de van Maanen puede, y probablemente lo hará, seguir radiando al ritmo actual durante 15 millones de millones de años sin perder más de una milésima parte de su peso actual.
¶ Notas
Esto se muestra en la fig. 15, siendo el área de la curva de 3000 grados sólo un dieciseisavo del área de la curva de 6000 grados. ↩︎
Las imágenes grandes y redondas de estrellas que se muestran en el frontispicio se deben simplemente a la sobreexposición y no tienen nada que ver con el tamaño de las estrellas. ↩︎
Por razones puramente prácticas la altura no se toma proporcional a la luminosidad sino a su logaritmo; sin algún dispositivo como este sería imposible representar el rango de más de 1.000.000 a 1 en las luminosidades observadas de las estrellas rojas. ↩︎
Esto proporciona una objeción adicional a la hipótesis de Russell, que, para evitar confusiones, no se mencionó en la p. 295. ↩︎